Теплоотдача при свободной конвекции

Вспомним определения.

Конвекция – перенос теплоты при перемещении макрообъёмов жидкости из области пространства с одной температурой в область с другой. Это один из трёх простых видов теплообмена.

Конвективный теплообмен – теплообмен в движущейся жидкости. Это сложный вид теплообмена, сочетание конвекции и теплопроводности.

Свободная конвекция – вид конвективного теплообмена, когда на жидкость не действуют внешние поверхностные силы, она движется за счёт неоднородности массовых сил, связанной обычно с различием плотностей нагретой и холодной жидкости. Подчеркнём, что свободная конвекция – вид конвективного теплообмена, а не конвекции.

Обычно массовыми силами являются силы тяжести – это естественная или свободно-гравитационная конвекция (ещё более точное название – термогравитационная). При этом жидкость, например, около горячего тела нагревается и расширяется, её плотность и удельный вес уменьшаются и нагретый объём поднимается вверх.

Уравнения процесса

Будем рассматривать стационарный процесс. Пусть внешние условия таковы, что если бы нагрева (или охлаждения) не было, то жидкость покоилась бы, имея исходную температуру , и плотность . При этом распределение давления в жидкости было бы гидростатическим с градиентом

. (1)

Сжимаемостью жидкости в случае свободной конвекции можно пренебрегать, считая, что не зависит от . Но зависимость от температуры как раз определяет свободную конвекцию, примем её линейной

, (2)

где – избыточная температура, – коэффициент температурного объёмного расширения, .

Уравнение движения возьмём в прежнем виде (К4)

. (3)

В этом уравнении слагаемые и много больше остальных, но они близки по величине, их разность мала и имеет тот же порядок, что остальные слагаемые. Это нужно использовать. Введём возмущение давления , то есть

, (4)

и рассмотрим указанную разность с подстановкой (2), (4) и, затем, (1):

.

Подставим это снова в (3), разделив всё уравнение на (с учётом ):

. (5)

Теперь все слагаемые имеют одинаковый порядок и уже описывают механизм движения при свободной конвекции. При этом очень близко к , поэтому их можно далее не различать (опуская индекс ₀). Кроме того, в уравнении осталось только (без ), и далее будем опускать у него индекс ₁ , понимая под возмущение давления.

Если учитывать, что вектор имеет проекцию только на ось ( , , ), можно увидеть, что в проекции на оси уравнения движения имеют прежнюю форму (К5), кроме проекции уравнения на ось

, где отличие только в первом слагаемом правой части.

После перехода к прежним (как перед (К10) ) безразмерным переменным , , , ( , – температура стенки), получим

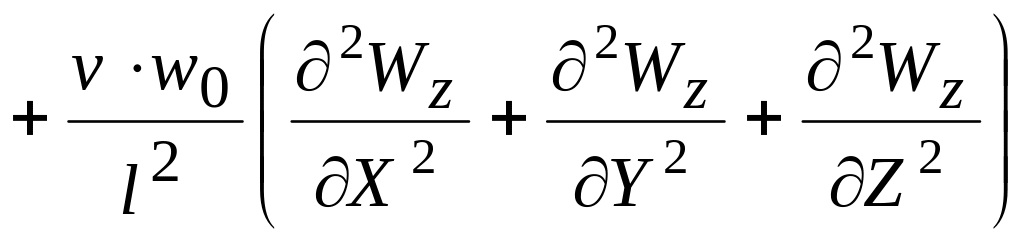, или, по аналогии с (К11)

.

Здесь, по сравнению с (К11), кроме прежних чисел подобия (число Рейнольдса) и (число Эйлера) появилось новое число подобия – число Грасгофа.

Число Gr характеризует влияние сил, связанных с температурными возмущениями плотности (точнее, удельного веса) по сравнению с силами вязкости.

При расчётах число Gr обычно является определяющим, то есть критерием подобия (вместе с Pr). Следует отметить, что в случае свободной конвекции нет заданной скорости , поэтому число Re является не заданным, а искомым, наряду с числами Nu и Eu.

Таким образом, в простых схемах с одним определяющим размером (вертикальная поверхность высотой , длинная горизонтальная труба диаметром ) уравнение подобия для теплоотдачи должно иметь вид

.

В более сложных схемах, вообще говоря, могли бы добавляться параметры , и т.д., характеризующие геометрию области. А в практических уравнениях – поправочные коэффициенты. В реальных уравнениях подобия для обычных сред основным определяющим фактором оказывается произведение – число Релея (Rayleigh), а не два отдельных числа Gr и Pr. Практические уравнения подобия стараются представить в степенной форме, так что типичная форма уравнения подобия для свободной конвекции имеет вид

,

где , – поправочные коэффициенты (один или несколько). Впрочем, при более точном рассмотрении зависимость от числа Pr учитывается отдельным множителем, так что уравнение подобия имеет структуру

.

Можно ещё добавить, что в типичных схемах, как оказалось, при свободная конвекция не проявляется, и имеет место чистая теплопроводность в покоящейся жидкости.

Свободная конвекция в неограниченном пространстве

Рассматривается стационарная теплоотдача от поверхности тела с температурой к большому (по сравнению с размерами тела) объёму жидкости с постоянной (вдали от тела) температурой . Для определённости будет считать, что у поверхности тела жидкость нагревается и расширяется, то есть . При охлаждении и сжатии картина будет точно такой же, но перевёрнутой “вверх ногами”.

1. Вертикальные поверхности

К этому случаю относятся плоские стенки, вертикальные трубы, боковые поверхности аппаратов и т.п. И качественно, и количественно теплообмен почти не зависит от формы и размеров сечения тела в горизонтальной плоскости.

Картина процесса. У стенки жидкость нагревается и поднимается вверх. В нижней части слой тонкий, движение ламинарное. С высотой погранслой утолщается и становится “локонообразным”, турбулентным.

Поперёк слоя скорость от нуля у стенки достигает максимума и снова убывает до нуля на внешней границе погранслоя (рис. ). Температура же убывает монотонно (рис. ). Коэффициент теплоотдачи в ламинарном слое убывает с высотой, потом растёт на переходном режиме и стабилизируется при турбулентном (рис. б).

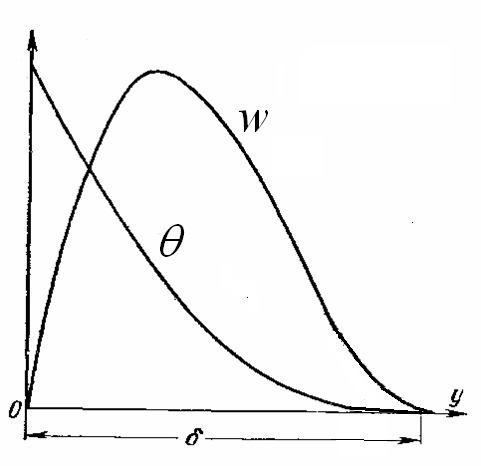
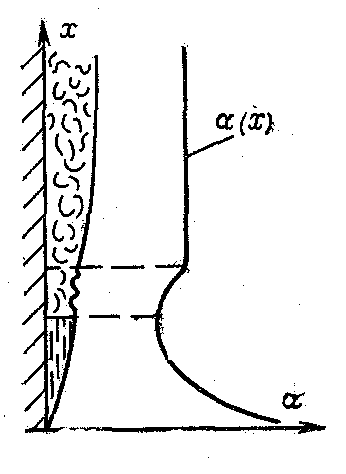
а б

Рис.

Уравнения подобия. Определяющая температура жидкости – вне движущегося слоя, используется для , кроме , – температура стенки. Определяющий размер – высота поверхности нагрева (то есть если стенка нагревается не по всей высоте, то не высота стенки!). Температурный напор .

Числа подобия 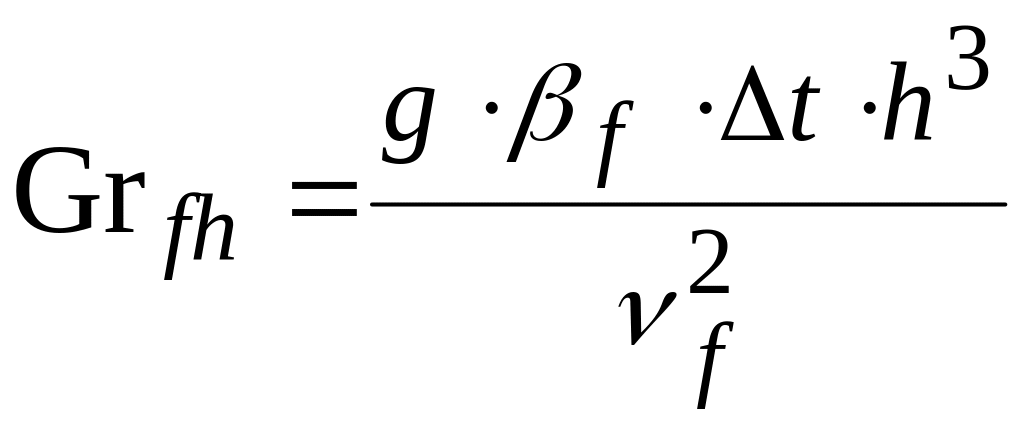; . Режим теплообмена определяется числом . Упрощенные уравнения подобия, без отдельного учёта влияния Pr, описываются так.

При конвекция не проявляется, теплообмен рассчитывают как чистую теплопроводность в неподвижной жидкости.

При имеет место ламинарный режим, вид уравнения

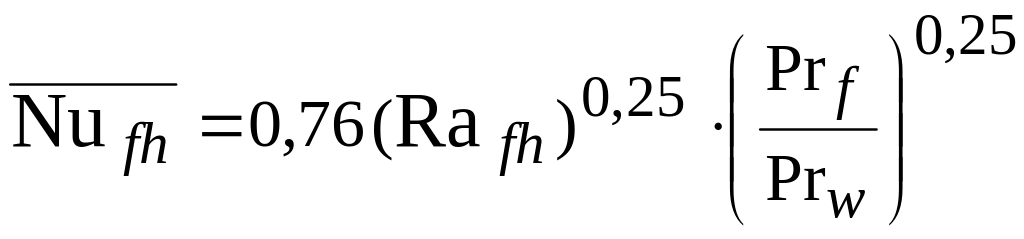. (6)

При – турбулентный режим:

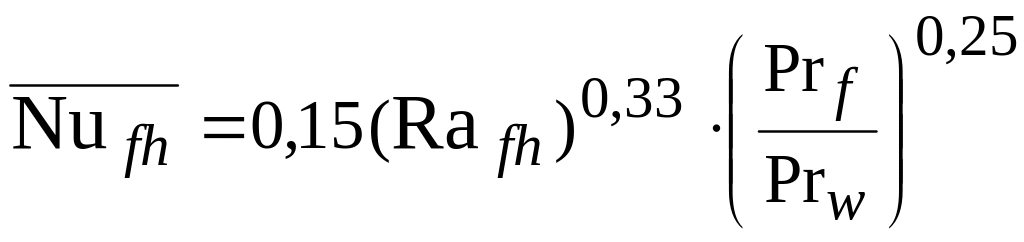. (7)

Замечания.

1. Для газов в этих уравнениях, как обычно, поправку на неизотермичность не применяют, считая приближённо . Так, для воздуха , тогда уравнения (6), (7) примут, соответственно, вид

,

.

2. Размер входит в число и в число в кубе . Поэтому из (6) следует, что на ламинарном режиме , то есть коэффициент теплоотдачи не очень сильно убывает с ростом высоты, а из (7) – что в турбулентном режиме не зависит от высоты.

3. Так как в число входит , то здесь зависит от температурного напора . Вспомним, что при вынужденной конвекции не зависит непосредственно от . Таким образом, тепловой поток по формуле Ньютона (К1) здесь пропорционален не , а на ламинарном или на турбулентном режиме. То есть вместо формулы (закона) Ньютона здесь логичнее было бы принимать степенную зависимость вида . Но по традиции в теории теплообмена принято использовать именно зависимость (К1) во всех случаях конвективного теплообмена.