13. Меры вариации признака, назначение, методы исчисления.

Вариация – различие в значениях к-л признака у разных единиц данной совокупности в один и тот же период или момент времени. Наличие вариаций является основой предпосылок статистического исследования. Они помогают познать сущность изучаемого явления. Наряду со средней (величина, которая дает обобщенную характеристику признака изучаемой совокупности, но не раскрывает ее строения) важное теоретическое и практическое значение имеет изучение отклонения от средней и от размера распределения, от которых зависит надёжность. Анализ показателей или меры вариации признака - показатели, характеризующие эти отклонения. К основным показателям вариации обычно относят: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратичное отклонения, коэф. вариации.

Для оценки вариации используют показатели:

1. Абсолютные:

- Размах вариации (размах колебаний) - важный показатель колеблемости признака, но он дает возможность увидеть только крайние отклонения, что ограничивает область его применения. R=Xmax-Xmin

Для более точной характеристики вариации признака на основе учета его колеблемости используются другие показатели.

- Среднее линейное отклонение đ представляет собой среднюю арифметическую абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю. Для сгруппированных данных:

x – варианта, - средняя, ∑f – сумма частот вариационного ряда.

- Дисперсия - средний квадрат отклонений от средней арифметической. Взвешенная дисперсия для вариационного ряда:

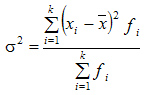
- Среднее квадратическое отклонение (СКО) – положительное значение квадратного корня из дисперсии. Показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения.

2. Относительные

Относительная величина в силу своей безразмерности позволяет сравнивать вариации различных величин, в т.ч. представленных в различных единицах измерения. Этот показатель характеризует степень надежности средних: чем меньше коэффициент вариации, тем надежнее представительная средняя.

-коэф. вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической.

Показатель вариации позволяет оценить количественную однородность совокупности по данному признаку. Принято считать, что если V ≤ 33%, то совокупность однородна по данному признаку.

14. Дисперсия и ее основные свойства.

Вычисление дисперсии по способу «моментов».

Дисперсия - средний квадрат отклонений от средней арифметической. Является основной мерой вариации.

 – средняя в целом по совокупности; f – частота в целом по совокупности.

Основные свойства дисперсии:

1)если все вариантные х уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия не изменится;

2)если все варианты х разделить или умножить на постоянное число b ≠ 0, то дисперсия соответственно уменьшится или увеличится в b² раз.

Если рассмотреть средний квадрат отклонения от некоторой постоянной с ≠ , то он будет > дисперсии на определенную величину ( - с)².

Тогда можно записать: б² = . Это равенство выполняется при любых значениях C, в т.ч. и при С = 0. - средний квадрат.

Получаем важную в теоретическом и практическом значении формулу: б² = ² – ( )²

– исправленная (несмещенная) дисперсия.

Вычисление дисперсии: используя рассмотренное свойство можно упростить вычисление дисперсии. В начале все варианты уменьшить на постоянную А, затем уменьшить в b раз. Тогда дисперсия определяется:

i — величина интервала ( i = b ); А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой (A = Xк); m1 - квадрат момента первого порядка; m2 - момент второго порядка

Этот способ расчета дисперсии и среднего квадратического отклонения называется способом моментов, или способом от условного нуля. Он выгоден в тех случаях, если исходная совокупность представлена в виде вариационного ряда распределения с равными интервалами.