11. Средние величины, виды средних.

Средней величиной в статистике называют обобщающий показатель по какому-либо признаку. Средняя показывает уровень этого признака, отнесенный к единице совокупности.

Среднее играет важнейшую роль в статистике, так как именно в ней находят свое проявление закономерности массовых явлений, их изменения в пространстве и во времени.

В статистике различают простые (невзвешанные) и взвешанные средние. Простые используются для усреднения несгруппированных данных, как правило, представленных абсолютными величинами, имеющими статистич.размерность – единица.

Взвешенная средняя используется для группировки данных.

Известны различные виды средних. В статистике наиболее часто используются степенные средние.

, где - средняя, - значение усредненного признака

Каждое такое отдельное значение называется вариантой. - знак суммы(суммирование)

m- целое,степень средней;n- объем(численность) совместимости.

В зависимости от m различают следующие виды средних:

1)m=2 – среднее квадратическое

- часто используется в теории измерений

2)m=1 – среднее арифметическое

3)m=0 – среднее геометрическое

Обычно используется для усреднения относительных величин.

4)m=-1 – среднее гармоническое

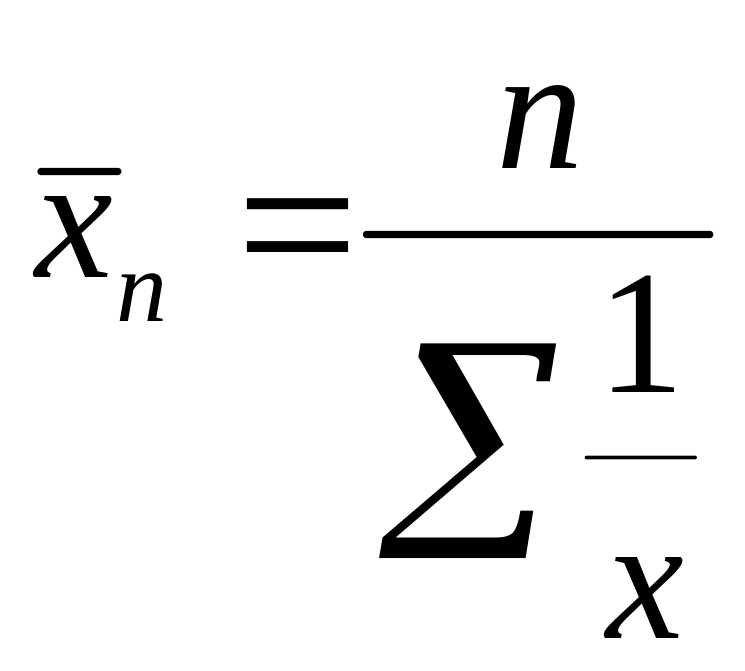
Используется в дополнение к средней арифметической при усреднение показателей со статистической размерностью больше 1. В частности, гармонические индексы как средние из индивидуальных в индексном анализе.

Для одних и тех же исходных данных разные средние имеют разные значения.

Чем больше степень средней, тем больше сама средняя. Этот факт в статистике получил название мажорантного свойства степенной средней.

Для того, чтобы правильно выбрать вид средней, рекомендуется составить логическую формулу, получившую название исходного соотношения средних (ИСС).

Если исходные решения представлены в сгруппированном виде, в виде вариационного вида, то f – частоты, - частости.

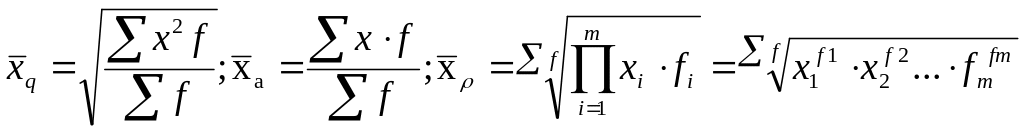
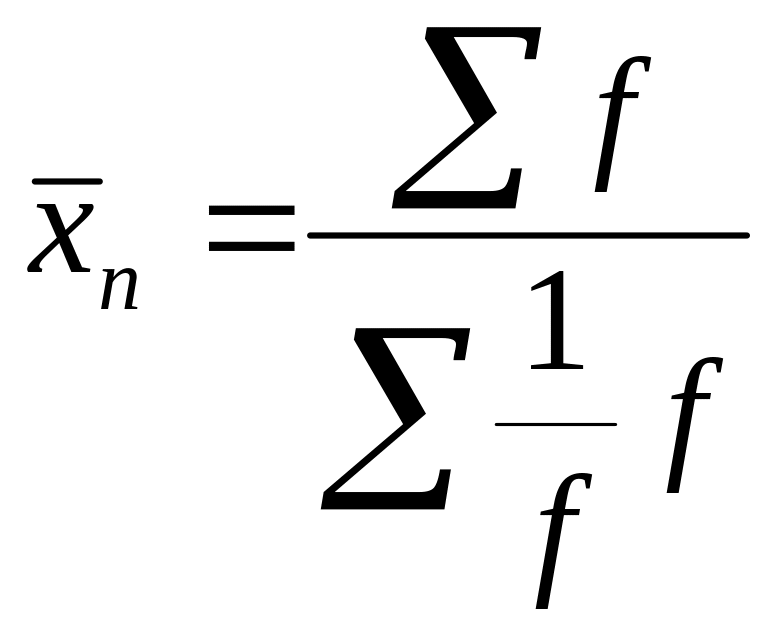
12. Средняя арифметическая и ее основные свойства. Построение средней по способу «моментов».

К основным свойствам средней относятся:

1) если все варианты Х уменьшить или увеличить на постоянное число А, то и средняя увеличится или уменьшится на эту постоянную.

2) если все варианты Х разделить или умножить на постоянную В, то и средняя увеличится или уменьшится в В раз.

3) если все веса f разделить или умножить на постоянную c ( c≠0), то средняя не изменится. Этим свойством часто пользуются для того, чтобы отобразить весы в виде относительной величины структуры.

4) сумма отклонений вариант от средней равно нулю. Это свойство означает, что средние арифметические взаимно компенсируют отклонения в большую или меньшую сторону.

Использую рассмотренные свойства можно упростить вычисления средних. В начале все варианты Х уменьшают на А, затем в В раз, получаем условное значение:

Такой упрощенный способ вычисления средних получил название способа моментов. Этот способ особенно удобен, если исходные данные представлены в виде вариационного ряда распределения (с равными интервалами). Тогда полагают: В=I,A= расположенному в середине ряда распределения или вблизи середины. Тогда, каковы бы ни были значения i или принимает значения: = ….-3,-2,-1,0,1,2,3….

Если совместимость разбита на группы и для каждой из групп вычислены средние (групповые средние) - объем i-ой группы, , то общая средняя может быть определена:

Т.е. общая средняя равна средней взвешанной из групповых средних, причем, весами являются объемы групп. В качестве весов могут быть использованы не только частоты или объемы групп,но и различные показатели. Весьма важно предварительно выяснить что есть признак фактов(учредняемый признак), и что есть признак – вес.