18. Безопасная палитра.

Термин безопасная палитра используют в Web-графике. Поскольку скорость передачи данных в Интернете пока оставляет желать лучшего, для оформления Web-страниц не применяют графику, имеющую кодирование цвета выше 8-разрядного. При этом возникает проблема, связанная с тем, что создатель Web-страницы не имеет ни малейшего понятия о том, на какой модели компьютера и под управлением каких программ будет просматриваться его произведение. Он не уверен, не превратится ли его "зеленая елка" в красную или оранжевую на экранах пользователей. В связи с этим было принято следующее решение. Все наиболее популярные программы для просмотра Web-страниц (броузеры) заранее настроены на некоторую одну фиксированную палитру. Если разработчик Web-страницы при создании иллюстраций будет применять только эту палитру, то он может быть уверен, что пользователи всего мира увидят рисунок правильно. В этой палитре не 256 цветов, как можно было бы предположить, а лишь 216. Это связано с тем, что не все компьютеры, подключенные к Интернету способны воспроизводить 256 цветов. Такая палитра, жестко определяющая индексы для кодирования 216 цветов, называется безопасной палитрой.

19. Алгоритмы вывода графических примитивов. Прямое вычисление координат.

Алгоритмы вывода прямой линии: Рассмотрим растровые алгоритмы для отрезков прямой линии. Предполо­жим, что заданы координаты (x 1 ,y 1 - х2,у2) концов отрезка прямой. Для вывода линии необходимо закрасить в определенный цвет все пикселы вдоль линии. Для того чтобы закрасить каждый пиксел, необходимо знать его ко­ординаты.

Наиболее просто нарисовать отрезок горизонтальной линии:

 

Вычисление текущих координат пиксела здесь выполняется как приращение по х (необходимо, чтобы х1 <-х2), а вывод пиксела обеспечивается функцией Пиксел(). Поскольку в языке С, C++ для названия функции нельзя использо­вать кириллицу, то будем дальше использовать ее как комментарий.

Аналогично рисуется отрезок вертикали:

 

Как видим, в цикле выполняются простейшие операции над целыми числа­ми — приращение на единицу и проверка на "< =". Поэтому операция рисо­вания отрезка выполняется быстро и просто. Ее используют как базовую операцию для других операций, например, в алгоритмах заполнения плоско­сти полигонов.

           Можно поставить такой вопрос: какая линия рисуется быстрее — горизон­таль или вертикаль? На первый взгляд — одинаково быстро. Если учитывать только математические аспекты, то скорость должна быть одной и той же при одинаковой длине линий, поскольку в обоих случаях выполняется равное количество идентичных операций. Однако если кроме расчета координат анализировать также вывод пикселов, то могут быть отличия. В растровых системах рисование пиксела обычно означает запись одного или нескольких бит в память, где сохраняется растр. И здесь уже не все равно — по строкам или по столбцам заполняется растр. Необходимо учитывать логическую ор­ганизацию памяти компьютера, в которой хранятся, биты или байты растра.

        Даже для компьютеров одного типа (например, персональных компьютеров) для различных поколений процессоров и памяти скорость записи по сосед­ним адресам может существенно отличаться от скорости записи по не сосед­ним адресам [40]. В особенности это заметно, когда для растра используется виртуальная память с сохранением отдельных страниц на диске и (или) в оперативной памяти (RAM). При работе графических программ в среде опе­рационной системы Windows часто случается так, что горизонтали рисуются быстрее вертикалей, поскольку в страницах памяти хранятся соседние байты. А может быть, что RAM достаточно, но скорости рисования все же различны.

Например, если используется черно-белый растр в формате один бит на пиксел, то для вертикали битовая маска одинакова для всех пикселов линии, а для горизонтали маску нужно изменять на каждом шаге. Здесь необходимо  заметить, что рисование черно-белых горизонталей можно существенно ускорить, если записывать сразу восемь соседних пикселов — байт в памяти.

            Горизонтали и вертикали представляют собой частный случай линий. Рассмотрим линию общего вида. Для нее также необходимо вычислять координат каждого пиксела. Известно несколько методов расчетов координат точек линии.

Прямое вычисление координат

 Пусть заданы координаты конечных точек отрезка прямой. Найдем координаты точки внутри отрезка (рис. 3.1).

 

 

 

 

В зависимости от угла наклона прямой выполняется цикл по оси х или по у

(рис. 3.2).

 

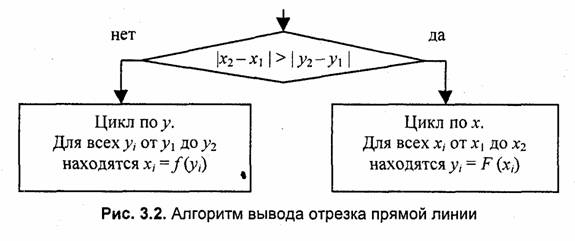
            Приведем пример записи этого алгоритма на компьютерном языке програм­мирования С, C++. Для сокращения текста рассмотрим фрагмент программы, где выполняется цикл по оси х, причем х1 <х2:

Здесь все операции выполняются над целыми числами. Двойные скобки не­обходимы для того, чтобы деление выполнялось после умножения. Недос­татки такой программы — в цикле выполняется много лишних операций, присутствуют операции деления и умножения. Это обуславливает малую скорость работы. Относительно лишних операций в цикле. Можно вынести вычисление (у2 - у 1)/(х2 – х1) из цикла, поскольку это значение не изменя­ется. Однако для этого уже необходимо использовать операции с плавающей точкой:

      Поскольку мы решили использовать операции с плавающей точкой, то по­пробуем еще уменьшить количество операций в цикле. Если раскрыть скобки в выражении у = у1 + (х – х1)-к; то получим у = у1 + х.к- х1 .к. Здесь значе­ние (yl – х1.к) является константой— эти операции также вынесем из тела цикла.

                         

 

В цикле выполняются только две арифметические операции и преобразова­ние х из целого в форму с плавающей точкой.

Если рассматривать цикл вычисления у, по соответствующим значениям х_i = х1, х1 +1, ... , х2 как итеративный процесс, то можно поставить такой вопрос: чему равна разность (у_i+1 — у_i)1 Она равна у_i+1 —у_i = xl + (х_i+1—xl)k-xl- (x_i – х1) к = (х_i+1 – x_i) к = к; поскольку x_i+1 – x_i =1. Разность (y_i+1 – у_i) — константа, равная к. Исходя из этого, можно построить цикл таким образом:

В теле цикла есть только одна операция для вычисления координаты у (если  не учитывать <=   и ++).

           Если сравнивать последний вариант с предыдущим, то последний лучше по быстродействию. Также существенно отличаются способы вычисления коор­динаты у. В последнем варианте значение у вычисляется прибавлением при­ращения к на каждом шаге, и на последнем шаге цикла (когда х=х2) долж­но стать у=у2. Исходя из чисто математических соображений здесь все кор­ректно, однако необходимо учесть, что в компьютере дробные числа представляются в формате с плавающей точкой не точно. Кроме погрешно­сти представления чисел существует ошибка выполнения арифметических операций с плавающей точкой. Ошибка зависит от разрядности мантисс, и самая малая — для long double, но все равно не нулевая. С каждым шагом цикла ошибки накапливаются, и может так произойти, что у не равно у2 на последнем шаге. Это необходимо учитывать при использовании алгоритма.

          Положительные черты прямого вычисления координат:

1.  Простота, ясность построения алгоритма.

2.   Возможность работы с нецелыми значениями координат отрезка.

Недостатки:

1.  Использование операций с плавающей точкой или целочисленных опера­ций умножения и деления обуславливает малую скорость. Однако это за­висит от процессора и для различных типов компьютеров может быть по-разному. В современных компьютерах, в которых процессоры используют эффективные способы ускорения (например, конвейер арифметических операций с плавающей точкой), время выполнения целочисленных опера­ций уже не намного меньше. Для старых компьютеров разница могла быть в десятки раз, поэтому и старались разрабатывать алгоритмы только на основе целочисленных операций.

2.   При вычислении координат путем добавления приращений может накап­ливаться ошибка вычислений координат.

Последнюю разновидность прямого вычисления координат, рассмотренную здесь, можно было бы назвать "инкрементной". Но такое название получили алгоритмы другого типа.