15. Знаки тригонометрических функций. Формулы сложения.
Формулы сложения
sin (α + β) = sin α · cos β + sin β · cos α
sin (α - β) = sin α · cos β - sin β · cos α
cos (α + β) = cos α · cos β - sin α · sin β
cos (α - β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)
16. Тригонометрические функции двойного и половинного аргумента. Формулы понижения степени.
Формулы двойного угла
cos 2α = cos² α - sin² α
sin 2α = 2sin α · cos α
tg 2α = (2tg α) ÷ (1 - tg² α)
ctg 2α = (ctg² α - 1) ÷ (2ctg α)
Формулы половинного угла.
Формулы понижения степени
17. Преобразование суммы и разности тригонометрических функций в произведение.
Тригонометрические функции, их свойства и графики.
СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК
а) Область определения: D (sin x) = R .
б) Множество значений: E (sin x) = [ – 1 , 1 ] . в) Четность, нечетность: функция нечетная.
г)
Периодичность:
функция периодическая с основным
периодомT =2
д) Нули
функции:
sin x =
0 при x =
n, n 
Z.
е) Промежутки знакопостоянства:
; 
.
ж) Промежутки
монотонности:
.
з) Экстремумы:
; 
.
СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК
а) Область определения: D (cos x) = R .
б) Множество значений: E (cos x ) = [ – 1 , 1 ] . в) Четность, нечетность: функция четная.
г)
Периодичность: функция
периодическая с основным периодом T
=2
д) Нули
функции:
cos x =
0 при x = 
+
n, n
Z.
е) Промежутки знакопостоянства:
;
.
ж) Промежутки монотонности:
;
.
з) Экстремумы:
; 
.
СВОЙСТВА ФУНКЦИИ y = tg x И ЕЕ ГРАФИК
а) Область определения: D (tg x) = R \ { /2 + n( n Z ) }.
б) Множество значений: E (tg x ) = R . в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T =
д) Нули функции: tg x = 0 при x = n, n Z.
е) Промежутки знакопостоянства:
;
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК
а) Область определения: D (ctg x) = R \ { n( n Z ) }.
б) Множество значений: E (ctg x ) = R . в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = д) Нули функции: ctg x = 0 при x = /2 + n, n Z.
е) Промежутки
знакопостоянства ;
; 
.
ж) Промежутки монотонности: функция убывает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
Обратные тригонометрические функции.
АРКСИНУС И ЕГО ГРАФИК
Функция x =
arcsin y
является обратной к
функции y =
sin x на
отрезке 
.
Для исходной и обратной
функций привычнее аргументы
и функцию обозначать
одними и теми же
буквами:
y = sin x, y = arcsin x.
В
таких обозначениях графики
указанных функций симметричны
относительно прямой y
= x.
Поэтому, нарисовав график
функции y =
sin x на
отрезке 
и
симметрично отобразив
его относительно прямойy
= x,
получим график арксинуса.
а) Область определения: D (arcsin x) = [ – 1, 1].
б) Множество значений: E (arcsin x) = .
в) Четность, нечетность: функция нечетная.
г) Нули функции: arcsin x = 0 при x = 0.
д) Промежутки знакопостоянства:
е) Промежутки монотонности: функция возрастает на всей области определения.
АРКОСИНУС И ЕГО ГРАФИК
Функция x = arccos y является обратной к функции y = cos x на отрезке x [ 0, ]. Для исходной и обратной функций привычнее аргументы и функцию обозначать одними и теми же буквами:
y = cos x, y = arccos x.
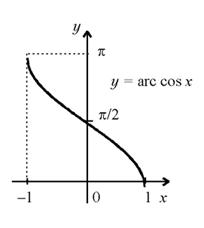
а) Область определения: D (arccos x) = [ – 1, 1].
б) Множество значений: E (arccos x) = [0, ].
в) Четность, нечетность: функция не является ни четной, ни нечетной.
г) Нули функции: arccos x = 0 при x = 1.
д) Промежутки знакопостоянства: arcсos x > 0 при x [– 1, 1).
е) Промежутки монотонности: функция убывает на всей области определения.
АРКТАНГЕНС И ЕГО ГРАФИК
Функция x =
arctg y
явлется обратной к функции, y =
tg x на
интервале
.
Для исходной и обратной функций привычнее аргументы и функцию обозначать одними и теми же буквами: y = tg x, y = arctg x.
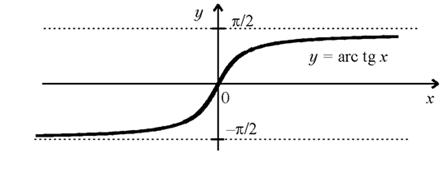
Свойства функции арктангенс y = arctg(x).
Область определения функции y = arctg(x):
.Область значений функции арктангенс:
.Функция арктангенс - нечетная, так как
.Функция возрастает на всей области определения, то есть, при .
Функция арктангенс вогнутая при
,
выпуклая при 
.Точка перегиба (0; 0), она же ноль функции.
Горизонтальными асимптотами являются прямые
при 
и 
при 
.
На чертеже они показаны зеленым цветом.
АРКОТАНГЕНС И ЕГО ГРАФИК
Функция x = arcctg y является обратной функции y =ctg x на интервале x (0, ). Для исходной и обратной функций привычнее аргументы и функцию обозначать одними и теми же буквами: y = ctg x, y = arcctg x .
а) Область определения: D (arcctg x) = R. б) Множество значений: E (arcctg x) = (0, ).
в) Четность, нечетность: функция не является ни четной, ни нечетной
г) Нули функции: нет.
д) Промежутки знакопостоянства: arcctg x > 0 при всех x.
е) Промежутки монотонности: функция убывает на всей области определения.