10. Неинерциальные системы отсчета. Силы инерции.

Неинерциальная система отсчёта — называется такая система отсчёта, которая движется ускоренно относительно инерциальной системы отсчета. Законы Ньютона выполняются только в инерциальных системах отсчета. Для того, что бы найти уравнение движения в неинерциальной системе отсчета, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.

Классическая механика постулирует следующие два принципа:

1) время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчета;

2) пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчета.

Понятие силы инерции. В практических целях для описания движения тел часто удобно использовать неинерциальные системы отсчета (НСО). Неинерциальность проявляется в наличии у тел и частиц дополнительных ускорений, которые не могут быть объяснены силовыми воздействиями со стороны других тел или полей.

Рассмотрим движение маятника, находящегося в положении равновесия, в неподвижной СО и в НСО, движущейся вдоль оси OX с ускорением ac. Видно, что в НСО, связанной с тележкой, второй закон Ньютона не выполняется. Действительно, в случае прямолинейного движения тележки сумма всех сил, действующих на шарик, равняется нулю m·g + N = 0, а он тем не менее движется с отличным от нуля ускорением a' = a - ac = -ac, где a - ускорение шарика в неподвижной СО.

Поскольку с точки зрения наблюдателя, находящегося на тележке, шарик движется с ускорением a', то можно считать, что на него действует некоторая дополнительная сила, сообщающая это ускорение. Данную силу назовем силой инерции Fи.

Сила инерции - сила, сообщающая телу дополнительное ускорение, которое не вызвано взаимодействием с другими телами или полями.

В случае поступательного движения НСО сила инерции равна: Fи = m·a' = -m·ac.

Сила инерции в случае рассмотрения движения тела в НСО, движущихся поступательно, обладает следующими свойствами:

пропорциональна ускорению;

пропорциональна массе тела;

направлена против вектора ускорения, с которым движется НСО.

С введением силы инерции закон движения маятника принимает вид, аналогичный второму закону Ньютона в НСО: m·a' = m·g + N + Fи. Сила инерции реально проявляется как мера воздействия на тела системы, поскольку вызывает их движение с ускорением. Можно предсказать результат физического действия этой силы на тела или частицы относительно НСО. Например, падение груза с полки при резком торможении поезда, изменение положения висящего на веревке шарика при ускорении тележки и т. п.

Уравнение динамики для НСО, движущихся поступательно. Закон движения в неинерциальных СО можно сформулировать в следующем виде: произведение массы тела на ускорение в НСО равно векторной сумме всех сил, действующих на данное тело относительно ИСО, и силы инерции ma' = F + Fи, где F - векторная сумма всех сил, действующих на частицу в ИСО.

Действительно, согласно второму закону Ньютона для ИСО, и закону преобразования ускорений в СО, движущихся поступательно, имеем:

m·a = F;

m·(a' + ac) = F;

m·a' = F - m·ac= F + Fи.

Отметим, что уравнения движения частицы можно упростить путем соответствующего выбора СО, в частности, описав движение в НСО, относительно которой ускорение частицы равняется нулю. В этом случае все силы, действующие на частицу, скомпенсированы, т.е. F + Fи = 0.

Сопоставление силы инерции и силы тяжести. Сравним свойства силы инерции в поступательно движущихся НСО со свойствами силы тяжести, равной произведению массы тела на ускорение свободного падения. Указанные силы обладают рядом общих черт:

значение и направление этих сил не зависят от точки пространства НСО;

обе силы пропорциональны массе тел. Тела с разной массой под действием этих сил движутся с одинаковым ускорением. В этом смысле сила инерции и сила тяжести однотипны. Разница заключается только в различных значениях ускорений, вызываемых действием этих сил. Рассмотрим пример. Для шарика, висящего на нити в перемещающейся вдоль прямой линии с постоянным ускорением тележке (см. рис 5.2), действие сил тяжести и инерции может быть заменено воздействием результирующей силы, которая равна их векторной сумме. Эту результирующую силу можно рассматривать как некую эффективную силу тяжести, равную произведению массы на ускорение g'.

Принцип эквивалентности Эйнштейна. Рассмотрим результаты следующего мысленного эксперимента. Пусть наблюдатель, находясь в кабине лифта, изучает свободное падение тел. Он видит, что свободные тела падают на пол с одинаковым ускорением. Исходя из общности свойств силы инерции и тяжести можно заключить, что наблюдатель, фиксируя падение тел разной массы с одинаковым ускорением, не сможет определить, чем вызвано данное ускорение - действием однородного поля силы тяжести находящейся вблизи лифта планеты или ускоренным поступательным движением лифта, поскольку закон движения в этих случаях одинаков.

Эйнштейн, обобщив результаты этого мысленного эксперимента на другие законы природы, высказал предположение, что никакими физическими опытами невозможно отличить однородное поле силы тяжести от соответствующего однородного поля силы инерции.

Заметим, что поле силы тяготения является однородным лишь в ограниченной области пространства, в частности, у поверхности планеты, т.е. в случае, когда расстояние между телом и поверхностью планеты много меньше ее радиуса.

Выдвинутое Эйнштейном предположение легло в основу постулата, представляющего собой принцип эквивалентности Эйнштейна.

Все физические явления в однородном поле силы тяжести происходят совершенно так же, как и в однородном поле сил инерции.

Глубокая аналогия между полем сил инерции и однородным полем силы тяжести послужила основой общей теории относительности.

Понятие центробежной силы инерции. Рассмотрим движение шарика, закрепленного на стержне, который равномерно вращается вокруг перпендикулярной ему оси, проходящей через один из ее концов, с постоянной угловой скоростью w (см. рис. 5.3). В ИСО XY шарик движется с нормальным ускорением an, обусловленным силой упругости стержня Fупр (центростремительной силой). В НСО, связанной с вращающимся стержнем, ускорение шарика отсутствует a' = 0, а равнодействующая сил, приложенных к нему, равна силе упругости и отлична от нуля (в вертикальном направлении действие сил тяжести и реакции стержня на изгиб скомпенсированы). Таким образом, второй закон Ньютона в выбранной НСО не выполняется.

Попробуем видоизменить этот закон, скомпенсировав равнодействующую силу некоторой дополнительной силой инерции. Исходя из вышеизложенного, имеем:

F + (-m·an) = m·a' = 0. Назовем слагаемое в скобках центробежной силой инерции Fи = Fцб. Тогда уравнение динамики примет вид, аналогичный второму закону Ньютона: F + Fцб = m·a' = 0. Из этого уравнения следует, что Из уравнения (5.5) следует, что если тело покоится относительно равномерно вращающейся системы отсчета, то векторная сумма всех сил, действующих на него, и центробежной силы инерции равна нулю. Это утверждение называется принципом Даламбера.

Центробежная сила инерции направлена против вектора центростремительного ускорения и равна по величине центростремительной силе:

Fцб = m·u2/r = m·w2·r.

Fцб = -m·w2·r·n

Центробежная сила инерции не характеризует какого-то взаимодействия, а обусловлена вращательным движением системы отсчета. Центробежная сила инерции и сила тяжести эквивалентны, если мы рассматриваем движение тел под воздействием этих сил в ограниченной области пространства, т.е. в области, где вектора силы не изменяются (например, около поверхности Земли). В общем случае силы инерции и тяжести различны по виду зависимости их величины от расстояния до оси вращения или центра гравитирующего тела, но обе эти силы вызывают движение тел с ускорением.

Понятие силы Кориолиса и причины ее возникновения. Рассмотрим равномерно вращающийся со скоростью wc стол (см. рис. 5.4), на котором расположено некоторое тело. В случае отсутствия трения между телом и столом он будет покоиться относительно Земли. В ИСО, связанной с Землей, выполняется второй закон Ньютона, т.к. векторная сумма всех сил, приложенных к телу, равняется нулю и оно находится в состоянии покоя.

В НСО, связанной со столом, тело движется с нормальным ускорением и на него действует центробежная сила инерции. Причем соблюдаются следующие условия:

a' = an, следовательно, ускорение направлено к центру вращения;

F = Fцб, следовательно, сила направлена от центра, т. е. против вектора ускорения an.

Второй закон Ньютона в НСО, связанной со столом, не выполняется. Для его корректировки по аналогии с предыдущими примерами требуется ввести дополнительную силу. Назовем ее силой Кориолиса.

В чем причина силы Кориолиса?

Во вращающейся системе отсчета в отличие от НСО, движущихся поступательно, соотношение между абсолютной, переносной и относительной скоростями и аналогичное соотношение для ускорений не однотипны. Для преобразования скоростей справедливо векторное уравнение u = u' + uп.

При перемещении тела из одной точки вращающейся системы в другую изменяется как переносная скорость uп, так и направление вектора относительной скорости u', что связано с поворотом осей координат НСО. Это вызывает появление дополнительного ускорения, называемого кориолисовым ускорением - aк, и, как мы покажем в дальнейшем, закон преобразования ускорений при переходе от ИСО к НСО примет следующий вид: a = a' + aс + aк, где aс - переносное ускорение. aк = 2·[w, u'], где w - вектор угловой скорости вращения НСО.

При описании движения в НСО закон преобразования ускорений примет вид (5.10):

a' = a - aс - aк. Ускорение aк можно связать с действием на тело некоторой дополнительной силы, называемой силой Кориолиса Fк. Действительно, умножив уравнение (5.10) на массу, получим:

m·a' = F + Fцб + Fк; Fк = -2·m·[w, u'].

Проявление действия силы Кориолиса:

размытие правых берегов рек северного полушария, текущих в южном направлении;

движение маятника Фуко. Маятник Фуко представляет собой массивное твердое тело, подвешенное на длинной нити. Если такой маятник вывести из положения равновесия, то он будет колебаться, совершая движение в некоторой плоскости. Действие силы Кориолиса вызовет медленное вращение этой плоскости относительно вертикальной оси;

наличие дополнительного бокового давления на рельсы, а следовательно, их неравномерный износ, возникающий при движении поездов.

Случай движения частицы в радиальном направлении относительно равномерно вращающейся НСО. Получим выражение для расчета Кориолисова ускорения в случае движения частицы в радиальном направлении. Пусть шарик A движется прямолинейно относительно стержня за счет силы упругости сжатой пружины. Стержень в свою очередь равномерно вращается вокруг оси OO' с угловой скоростью w (см. рис. 5.5). Относительно ИСО движение шарика будет непрямолинейным и неравномерным. Траектория представляет собой спираль. Чтобы найти силы инерции, действующие на шарик в НСО, связанной с вращающимся стержнем, сначала определим его ускорение относительно ИСО.

На рис. изображены составляющие векторов скорости шарика в ИСО в различные моменты времени, разделенные интервалом dt. Эти составляющие представляют собой относительную u' и переносную uп скорости. Относительная скорость связана с движением шарика во вращающейся СО, а переносная - с движением НСО относительно лабораторной ИСО. Абсолютная скорость u движения шарика в неподвижной системе рассчитывается с помощью уравнения u = u' + uп.

И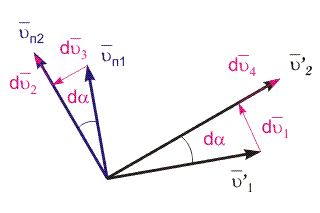зобразим составляющие вектора абсолютной скорости u в моменты времени 1 и 2 исходящими из одной точки .Найдем приращения относительной и переносной скоростей в разных точках ИСО, расположенных на расстояниях R и (R + dR) от оси вращения, имея в виду, что для малых углов da выполняются следующие скалярные равенства: da = w·dt; uп1 = w·R; uп2 = w·(R +dR); dR = u'·dt; |u2'| - |u1'| = |du'| = d|u'|, следовательно, du4 = du'.

Вектора du1 и du2 перпендикулярны радиусу и определяют тангенциальное приращение скорости. Вектора du3 и du4 коллинеарны радиальному направлению и определяют нормальное приращение скорости. Просуммировав все приращения скоростей с учетом их направлений и разделив результат на dt, получим выражение для расчета вектора ускорения в ИСО:

a = 2[w, u'] + w2·R·n - du'/dt·n = aк + aс + a',

где aк = 2[w, u']- Кориолисово ускорение, параллельное вектору t;

aс - переносное (центростремительное) ускорение; a' - относительное ускорение

Преобразовав формулу, получим выражение для расчета ускорения в НСО:

a' = a - aс - aк = a + aцб - aк.

Следовательно, для НСО 2 закон Ньютона запишется в виде:

m·a' = F + Fцб + Fк,

где Fк = -m·aк - сила Кориолиса; Fцб - центробежная сила инерции;

F - равнодействующая сил, приложенных к частице в ИСО

Случай движения частицы по окружности (тангенциальное направление). Получим выражение для кориолисова ускорения в случае движения тела по окружности с относительной скоростью u' = [w', R]. Ее угловая скорость относительно лабораторной ИСО равна: wл = w' + w, где w - скорость вращения НСО относительно ИСО; w' - угловая скорость вращения тела относительно НСО.

Для расчета абсолютного ускорения получим следующее выражение:

a = (w' + w)2·R = 2·w·w'·R + w2·R + w'2·R = aк + aс + a'.

Так как движение тела в ИСО происходит по окружности с постоянной по величине скоростью, то все составляющие ускорения направлены вдоль радиуса. Следовательно, для кориолисова ускорения с учетом направления мы получим выражение, аналогичное ранее приведенному для случая радиального движения тела.

Общий случай произвольного движения частицы в равномерно вращающейся СО. В случае произвольной ориентации вектора относительной скорости u' вектор кориолисова ускорения можно разложить на нормальную и тангенциальную составляющие, для вычисления которых справедлива одна и та же формула. Таким образом, в случае произвольно движущейся частицы в равномерно вращающейся НСО будет справедливо соотношение: aк = aкn + aкt = 2·[w, (un' + ut')] = 2·[w, u'].

Еще раз напомним причины, обуславливающие наличие кориолисова ускорения:

изменение направления вектора относительной скорости, связанное с вращательным движением НСО относительно ИСО;

изменение величины вектора переносной скорости, связанное с поступательным движением тела относительно НСО.

Особенности сил инерции. Рассмотрев различные силы инерции, можно заключить, что все они имеют общие черты и одновременно обладают рядом особенностей, по сравнению с силами, действующими в ИСО

не характеризуют какого-либо физического взаимодействия, следовательно, не подчиняются третьему закону Ньютона (для них не существует противодействующих сил). Силы инерции всегда являются внешними. Внутри системы нет физических объектов, которые были бы материальными источниками сил инерции;

силы инерции существуют исключительно в НСО и проявляются только как мера воздействия на тела системы;

пропорциональны массе тела.