26. Фазовые переходы. Уравнение Клайперона-Клаузиуса.

Фазовые переходы 1-ого рода.

Равновесное состояние однородного тела определяется заданием каких-либо двух термодинамических величин, например, p и T. Однако нет никаких оснований утверждать, что при всякой заданной паре значений этих величин тепловому равновесию будет соответствовать именно однородное состояние тела. Может оказаться, что при тепловом равновесии тело разбивается на соприкасающиеся однородные части, находящиеся в различных состояниях.

Такие состояния вещества, которые могут существовать одновременно в равновесии с друг другом, соприкасаясь между собой, называются различными фазами вещества.

Условия равновесия фаз .

Получим формулу Клайперона-Клаузиуса.

Продифференцируем по температуре условие равенства химических потенциалов: ,

Поскольку термодинамический потенциал , для изменения термодинамического потенциала имеем ,

, следовательно или -уравнение Клайперона-Клаузиуса.

27. Диаграммы состояния вещества.

При описании состояния вещества и его фазовых переходов обычно используются переменные P и T, в которых изображаются кривые равновесия при фазовых переходах данного вещества. Диаграмма, построенная в этих переменных, называется диаграммой состояния. Каждой точке на этой диаграмме соответствует определенное равновесное состояние. Она позволяет определить, какие фазовые переходы происходят при тех или иных процессах.

Рассмотрим случай термодинамической системы, в которой в равновесии находятся сразу три фазы однородного по физико-химическим свойствам вещества (например: лед, вода и пар). Равновесие такой системы будет наблюдаться при одновременном выполнении трех условий, соответствующих равновесию этих фаз между собой. Эти условия в общем виде можно записать в форме . Равенства приводят к системе из двух независимых уравнений ;

Решение этой системы уравнений при условии отсутствия химических превращений дает совершенно определенные значения давления и температуры, при которых три фазы могут существовать одновременно. Точка на диаграмме состояния в переменныхP и T, соответствующая указанным значениям давления и температуры, называется тройной точкой. В этой точке встречаются кривая плавления 1, разделяющая твердую и жидкую фазы, кривая испарения 2, разделяющая жидкую и газообразную фазы, и кривая возгонки 3, разделяющая твердую и газообразную фазы.

1 - кривая плавления, 2 - кривая испарения, 3 - кривая возгонки

Кривая испарения 2 заканчивается критической точкой (К), в которой исчезают отличия жидкой и газообразной фаз. Если фазовый переход осуществляется в обход критической точки, как показано пунктирной линией, то пересечения кривой испарения не происходит и фазовое превращение проходит путем непрерывных изменений без образования границы раздела фаз.

Для однородного по своим физико-химическим свойствам вещества в равновесии одновременно могут находиться не более трех фаз. Это означает, что для равновесной системы могут существовать только точки, в которых сходятся три фазы вещества, например, соответствующие трем его агрегатным состояниям. Точки, в которых могли бы одновременно существовать более трех фаз, не реализуемы.

Вещество в трех различных агрегатных состояниях может наблюдаться и при значениях температуры и давления, не соответствующих тройной точке. Например, в природе при различных погодных условиях наблюдаются одновременно лед, вода и водяной пар (последний, как правило, косвенным образом). Однако, в отличие от состояния в тройной точке, указанные состояния не являются равновесными, и для них характерен постоянный переход вещества из одной фазы в другую.

Значения давления и температуры в тройной точке для различных веществ очень стабильны, что позволяет использовать тройную точку для калибровки различных температурных шкал. Тройная точка воды используется в качестве основной реперной точки для температурных шкал Кельвина и Цельсия.

Как правило, все твердые вещества имеют несколько фазовых состояний, обусловленных различными кристаллическими модификациями, структурно отличающимися между собой. Эти фазы могут точно так же находиться в состоянии равновесия между собой, как и фазы, связанные с различными агрегатными состояниями. На диаграмме состояния условиям равновесия этих фаз соответствуют кривые равновесия при фазовых переходах. Существуют тройные точки, в которых могут одновременно находиться в равновесии три фазы, две из которых представляют собой кристаллические модификации, а одна либо жидкая, либо газообразная. У некоторых веществ тройные точки наблюдаются при равновесии трех различных кристаллических модификаций.

Свойство вещества иметь несколько кристаллических модификаций называется полиморфизмом. Этим свойством, например, обладают сера, углерод, олово и железо. Лед имеет несколько кристаллических модификаций. Фазовый переход из одной кристаллический модификации в другую называется полиморфным превращением, которое в большинстве случаев является фазовым переходом первого рода и сопровождается поглощением или выделением теплоты.

Для различных кристаллических модификаций характерно существование метастабильных состояний, то есть таких состояний, при которых одна фаза существует в области температур и давлений другой фазы. Такие же метастабильные состояния существуют и для фазовых переходов из одного агрегатного состояния в другое вблизи тройной точки.

На рис. схематически изображены области метастабильных состояний при фазовом переходе жидкость-газ. Выше линии 2 находится область, соответствующая переохлажденному пару, а ниже - перегретой жидкости. Вещество в указанных метастабильных состояниях используется в таких физических приборах как камера Вильсона и пузырьковая камера, принципы работы которых рассматриваются ниже.

Д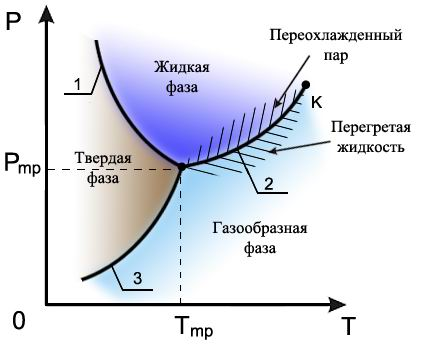иаграмма метастабильных состояний при фазовом переходе жидкость-газ

1 - кривая плавления, 2 - кривая испарения, 3 - кривая возгонки

Если изобразить изотермы двухфазной системы жидкость-газ , то горизонтальная часть изотерм будет соответствовать фазовому переходу вещества, справа от горизонтальной части лежат изотермы газовой фазы, а слева - жидкой. Пунктирные линии соответствуют метастабильным состояниям. Справа - переохлажденный пар, слева - перегретая жидкость. Эти состояния будут возникать в том случае, если зародыши другой фазы (капли и пузырьки соответственно) отсутствуют или у них имеется тенденция к исчезновению. Так как образованию зародышей способствуют всякого рода примеси и неоднородности, то метастабильные состояния свойственны хорошо очищенным веществам.

Так как давление переохлажденного пара превышает давление насыщенного пара при той же температуре, то такой пар называется пересыщенным. Образование и рост зародышей жидкой фазы в таком паре будет зависеть от многих факторов и в первую очередь от размеров зародышей, температуры и степени пересыщения. Степень пересыщения определяется как отношение плотности пересыщенных паров к плотности насыщенных паров , а при адиабатическом расширении она может быть рассчитана с помощью соотношения , где: P1, V1 и P2, V2 - начальные и конечные давления и объемы пара.

Опыты, проведенные в середине XIX века показали, что если в паре содержатся частицы пыли, то даже при небольшом пересыщении образуется туман и происходит переход из точки А в точку В. Такой процесс происходит в атмосфере, когда потоки, вызванные конвекцией, поднимают вверх воздух, содержащий водяной пар, где происходит его расширение, сопровождающееся уменьшением температуры. Это приводит к возникновению тумана и росту дождевых капель за счет избыточной концентрации пара по сравнению с насыщенным состоянием.

В 1870 г. Томсоном (лордом Кельвином) было показано, что вследствие поверхностного натяжения давление насыщенного пара над поверхностью капли, имеющей радиусr, больше, чем давление пара над плоской поверхностью жидкости, причем они связаны соотношением, где:- поверхностное натяжение,и- молярная масса и плотность жидкости,- абсолютная температура,R - универсальная газовая постоянная. Отсюда следует, что, если степень пересыщения пара превосходит величину, задаваемую правой частью соотношения, капли будет расти и образуется туман.

Чем мельче капли, тем большее пересыщение требуется для того, чтобы эти капли не испарялись, а росли. Для воды при имеем, то есть молекулы, как правило, не могут являться центрами конденсации. Однако эксперимент показывает, что прив водяных парах начинает образовываться туман. Английский физик Джозеф Джон Томсон (1856 - 1940) объяснил это тем, что вследствие взаимодействия (коагуляции), молекулы воды образуют капли, наибольший размер которых, что соответствует. При меньших значениях туман возникает только тогда, когда есть посторонние включения, например, пыль.