23. Гравитационное поле

Гравитационное поле - поле, которое создает вокруг себя тело, обладающее массой. Посредством гравитационных полей взаимодействуют физические объекты.

В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:

отклонение закона тяготения от ньютоновского;

запаздывание потенциалов, связанное с конечной скоростью распространения гравитационных возмущений; появление гравитационных волн;

эффекты нелинейности: гравитационные волны имеют свойство взаимодействовать друг с другом, поэтому принцип суперпозиции волн в сильных полях уже не выполняется;

изменение геометрии пространства-времени;

возникновение черных дыр;

Механизм взаимодействия гравитационных полей

Гравитационные массы пробного и тяжелого тела обладают свойством быть заряженными значением одного фундаментального знака заряда. Формула тяготения Ньютона оставляет открытым вопрос о механизме притяжения двух тел одного значения заряда.

Если тело рассматривать в комплексном пространстве, то знак заряда его поля определяется знаком изолированного направления. В простейшем случае можно рассмотреть изолированные направления в комплексных координатах В этих координатах имеем одинаковый знак заряда в двух вариантах изолированного направленияОбменные кванты как мера энергии поля также имеют два варианта направления положительного заряда (в верхнюю и нижнюю полусферу координат) Гравитационное поле складывается из энергий полей, мерой которых служит обменный квант. В комплексном виде обменные кванты пробного и тяжелого тел равнырассмотрим движение обменного кванта по циклонной кривойи по изолированному направлению в пробном теле В точке входа в изолированное направление пробного тела величину суммарного обменного кванта рассматриваем во первых как сумму(как взаимодействие полей верхней полусфер пробного и тяжелого тела), так и сумма. Модульпоэтому потенциальная сила, действующая со стороны поля на пробное тело, направлена вниз. Потенциал при обменном квантевыше потенциала при обменном квантеПробное тело переходит на новый радиус взаимодействия. Аналогично рассмотрим выход из изолированного туннеля пробного тела.

На выходе имеем взаимодействие нижней полусферы пробного тела с верхней и нижней полусферой тяжелого тела, в результате по величинам обменных квантов получим ценивая по модулю величины обменного кванта на выходе из изолированного туннеля пробного тела, вновь получим движение масс под действием потенциальных сил в сторону тяжелого тела. Таким образом, происходит “зашнуровывание“ (термин взят из ядерной физики) взаимодействующих тел в одной структуре.

Инерциальная масса тела, как было показано, определяется комплексом , где. Модуль инерционной массы не зависит от знака обменного кванта (вычитается он из кванта тяжелого тела или складывается с ним), поэтому рассмотренные варианты взаимодействия полей сводятся в расчетах к одному.

Рассчитаем величину дискретного сдвига пробного тела относительно тяжелого.

Взаимодействие происходит непрерывным образом, однако формулы отсекают конкретные дискретные значения. За начальные исходные параметры принимаем . Исходя из этих значений, определяем инерционные массы по формулам. Инерционные массы при переходе в расчете к новым текущим параметрам в формуле потенциала Ньютона становятся гравитационными, поэтому определяем их произведение и сумму, которые входят в рекуррентное соотношение.

Произведение дает

В результате рекуррентное соотношение принимает вид

Сокращения дают

Далее

Откуда окончательно будем иметь

Дальше можно провести расчет уже с новыми значениями параметров и определить В итоге получается ряд с более высокими степенями отношений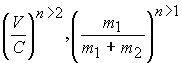. Преобразуем формулу, введя значение скоростиТаким образом, показано, что формула тяготения Ньютона определяет движение пробного тела в поле тяготения тяжелого тела при каждом фиксированном расстоянии на величину равную гравитационному радиусу пробного тела. Это геометрический квант движения. Расстояние изменяется и процесс продолжается.

Смещение пробного тела массой в гравитационном поле тяжелого тела массойна дискретную величинув соответствии с фиксированным расстояниемпри взаимодействии по формуле тяготения Ньютона.