18. Принцип относительности. Законы сохранения в сто.

При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения. Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта. Впервые явно использован в статье Г.А.Лоренца 1904 г.: "Положение вещей было бы удовлетворительным, если бы можно было с помощью определенных основных допущений показать, что многие электромагнитные явления строго, т.е. без какого-либо пренебрежения членами высших порядков, не зависят от движения системы. ... На скорость налагается только то ограничение, что она должна быть меньше скорости света" (Принцип относительности. Сборник работ классиков релятивизма. М.,1935. С.19) Выражен в 1905 г. в статье А.Пуанкаре "О динамике электрона", называющего его "постулат относительности Лоренца" и в статье А.Эйнштейна "К электродинамике движущихся тел", приписывающего изобретение принципа себе. Как писал Г.А.Лоренц в 1912 г., "Заслуга Эйнштейна состоит в том, что он первый высказал принцип относительности в виде всеобщего строго и точно действующего закона" (Принцип относительности. М.,1935. С.23).

Различают принцип относительности Эйнштейна (который приведён выше) и принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов механики.

Отцом принципа относительности считается Галилео Галилей, который обратил внимание на то, что находясь в замкнутой физической системе, невозможно определить, покоится эта система или равномерно движется. Во времена Галилея люди имели дело в основном с чисто механическими явлениями. Идеи Галилея нашли развитие в механике Ньютона. Однако с развитием электродинамики оказалось, что законы электромагнетизма и законы механики (в частности, механическая формулировка принципа относительности) плохо согласуются друг с другом. Эти противоречия привели к созданию Эйнштейном Специальной теории относительности. После этого обобщённый принцип относительности стал называться «принципом относительности Эйнштейна», а его механическая формулировка — «принципом относительности Галилея».

Понятие релятивистской энергии. Рассчитаем величину изменения некоторой физической величины, которая обусловлена работой всех сил, действующих на частицу, т.е. является аналогом кинетической энергии в классическом случае. В качестве исходного уравнения движения используем основной закон релятивистской динамики (17.13). Умножив уравнение (17.9) скалярно на вектор скорости частицы υ, получим:

Проведем ряд преобразований. Путем дифференцирования можно доказать справедливость соотношения:

Из этих выражений следует, что

Умножим это уравнение на величину dt. Используя выражение для расчета работы всех сил dA на элементарном перемещении dr, получим что:

Согласно этому величина E, равная E = m·c2/(1 - β2)1/2 = g·m·c2, имеет размерность энергии. Рассмотрим физический смысл величины E. Для этого найдем проекцию 4-вектора энергии-импульса на ось времени в пространстве Минковского. Ее величина равна Pt = m·dRt/dt0 = g·m·c·dt/dt = g·m·c.

Таким образом, с точностью до постоянного множителя “c” значение физической величины E равно проекции Pt. Величина E называется релятивистской энергией частицы.

Релятивистская энергия равна произведению проекции 4-вектора энергии-импульса на скорость света.E = Pt·c = g·m·c2.

Проведя суммирование уравнений по всем частицам системы, получим, что за конечный промежуток времени DE = A, т.е.

изменение релятивистской энергии системы равняется работе всех сил, действующих на эту систему. Рассмотрим как преобразуются релятивистская энергия и импульс при переходе к другим ИСО. Поскольку величины pрел и E являются проекциями ковариантной величины - 4-вектора энергии-импульса P = {Pt, Px, Py, Pz} = {E·c, pрел x, pрел y, pрел z},

то уравнения их преобразований должны быть аналогичны преобразованиям Лоренца. При этом компоненты pрел x, pрел y, pрел z преобразуются как x, y, и z, а компонента Pt = E·c, как время t. Таким образом,

Закон сохранения релятивистской энергии. Обобщив выражение (17.20) на систему невзаимодействующих частиц, можно сформулировать закон сохранения энергии в релятивистском случае.

Для замкнутой системы невзаимодействующих частиц релятивистская энергия остается постоянной.

Можно показать, что закон сохранения энергии распространяется также и на случаи распада и столкновения частиц, происходящие в замкнутых ИСО.

Обратите внимание, что энергия взаимодействия в величину релятивистской энергии не входит. Более того, понятие потенциальной энергии, определяемое конкретным видом взаимодействия частиц, в релятивистской механике не используется. Это обусловлено тем, что конечная скорость распространения взаимодействия не позволяет привести в соответствие изменение положения частиц системы и величину потенциальной энергии, определяемой соответствующими силами и зависящей от взаимного расположения частиц, и следовательно, корректно задать значение потенциальной энергии системы применительно к данному моменту времени.

Релятивистский импульс. Установим физический смысл вектора pрел. Для этого обобщим понятие классического импульса на четырехмерный (релятивистский) случай. Естественным обобщением понятия трехмерного вектора импульса p = m·u в евклидовом пространстве будет четырехмерный вектор P в пространстве Минковского P = m·dR/dt0 = {Pt, Px, Py, Pz}, где dR = {c·dt, dx, dy, dz} - 4-вектор расстояния в пространстве Минковского.

Поскольку P есть комбинация инвариантов массы m0, собственного времени dt0 и 4-вектора dR, то он является 4-вектором.

Исходя из этого пространственные проекции ковариантной величины - 4-вектора энергии-импульса - образуют трехмерный вектор pрел, называемый релятивистским импульсом: pрел = {m·dx/dt0, m·dy/dt0, m·dz/dt0} = m·dr/dt0 = g·m·dr/dt = g·m·u.

В отличие от классического случая релятивистский импульс зависит от скорости движения частицы не по линейному закону (см. рис. 17.2). Чем ближе скорость частицы к скорости света, тем больше отклонение релятивистского импульса от классического. Тем не менее классический и релятивистский импульсы имеют ряд общих черт:

сохраняются для свободных частиц, т.к. согласно определению (17.12), если u = const, то и pрел = const;

являются аддитивными величинами;

совпадают по величине и направлению при малых скоростях движения частиц.

Основной закон релятивистской динамики. Воспользовавшись уравнением 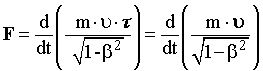и определением релятивистского импульса, получим основной закон релятивистской динамики (релятивистское уравнение движения):F = dррел/dt.

корость изменения релятивистского импульса частицы равна результирующей всех сил, действующих на нее.

Из уравнения 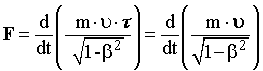следует, что за счет действия конечной силы можно получить лишь конечное приращение скорости, т.е. невозможно разогнать частицы до скоростей, равных скорости света. В современных ускорителях удается разогнать заряженные частицы до значений u, приближающихся к скорости света и отличающихся от нее всего на доли процента.

Уравнение движения F = dррел/dt. по форме совпадает с основным уравнением классической динамики F = dp/dt. Однако его физический смысл иной. В правой части уравнения F = dррел/dt. стоит производная от релятивистского импульса частицы, зависящего от ее скорости не по линейному закону pрел = {m·dx/dt0, m·dy/dt0, m·dz/dt0} = m·dr/dt0 = g·m·dr/dt = g·m·u.

Основной закон релятивистской динамики позволяет по известной зависимости скорости изменения релятивистского импульса определить силу, действующую на частицу, или, зная силу и воспользовавшись начальными условиями, решить задачу о нахождении зависимости r(t).

Основной закон релятивистской динамики инвариантен по отношению к выбору ИСО, а ИСО инвариантны по отношению к основному закону релятивистской динамики, что удовлетворяет принципу относительности Эйнштейна.

В релятивистском случае, в отличие от классического, сила зависит от выбора ИСО, т.е. не является абсолютной величиной. Она видоизменяется в соответствии с преобразованиями Лоренца.

Закон сохранения релятивистского импульса системы. Рассмотрим систему, состоящую из невзаимодействующих частиц. Проведя суммирование уравнений типа F = dррел/dt. по всем объектам системы, получим уравнение, аналогичное ему, но уже относящееся ко всей системе в целом.

Скорость изменения релятивистского импульса системы невзаимодействующих частиц равна векторной сумме всех сил, действующих на нее.

Отсюда вытекает закон сохранения релятивистского импульса, справедливый для частиц, движущихся с произвольными скоростями, и применимый в любых системах отсчета:

Релятивистский импульс замкнутой системы невзаимодействующих частиц сохраняется.

В этом заключается еще одно сходство релятивистского и нерелятивистского импульса. Закон сохранения импульса является фундаментальным и справедлив не только для механических систем.