16. Следствия из Преобразований Лоренца

1. Если в одной системе отсчета некоторые события происходят в точках x1 и x2 в один и тот же момент вр емени t, то в другой системе отсчета эти события происходят в точках x'1 и x'2 в разные моменты времени t'1 и t'2:

Понятие одновременности оказывается зависящим от выбора системы отсчета.

2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсче та между этими же событиями проходит время

Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах.

3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина

Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциа льные системы отсчета.

4. Если в одной системе отсчета тело имеет скорость v = (vx, vy, vz), то его скорос ть v' = (v'x, v'y, v'z) в другой системе отсчета равна

или в трехмерной векторной форме

5. Из соотношени (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии v2=(vx)2+(vy) 2+(vz) 2=c2, (n6)

получим

v'2=(v'x)2+ (v'y)2+(v'z) 2=c2. (n7)

Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v' в общем случае различны в разных системах отсчета.

Постоянство скорости света - следствие преобразований Лоренца

17. Преобразование скоростей в сто.

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна а скорость системы отсчёта S' относительно системы отсчёта S равнато скорость тела в при переходе в систему отсчёта S' будет равна. Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S' необходимо использовать преобразования Лоренца для скоростей:в предположении, что скоростьнаправлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Закон сложения скоростей

Рассмотрим малое тело, движущееся в инерциальной системе отсчета k со скоростью u. Пространственно-временные координаты этого тела (t, r). Перейдем в другую инерциальную систему отсчета k' , начало координат которой движется относительно начала координат системы k со скоростью b. Найдем скорость u' этого тела в системе k'.

Запишем преобразования Лоренца-Фока для дифференциалов координат:

Введем вспомогательные величины r 0 = r -ut и r'0 = r' -u't'. Разделим почленно второе и третье равенство на первое:

Полученные выражения связывают скорость тела, измеренную в системе k в пространственно-временной точке (t , r), со скоростью, измеренной в системе k' в той же мировой точке с координатами (t', r').

Полученные выражения удобны для анализа свойств преобразований Лоренца-Фока, но неудобны дл практических расчетов, так как левые части равенств (F23) содержат скорость в неявном виде (через r'0).

Выразим координаты r' 0 через r0 . Для этого запишем преобразования Лоренца-Фока , подставив в левую часть координаты (t'=0, r'=r'0):

С учетом первого равенства (F24) и определени r0 =r-ut, получаем

Подставляя полученные выражения в правые части (F24), имеем

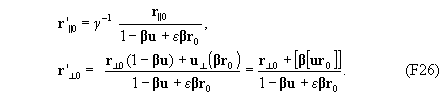
Теперь можно переписать равенства (F23)

Несмотря на громоздкость, полученные соотношени удобны для непосредственных вычислений - подставляя в правые части равенств (F27) значения скорости тела в некоторой мировой точке (t, r) мы получаем скорость тела в произвольной инерциальной системе отсчета в той же мировой точке.