
Резистивный элемент.
2.5.1. Пусть ток в резисторе:
![]() .
.
Мгновенное значение напряжения на резисторе:
![]()
Векторы тока и напряжения на резисторе приведены на рис. 2.4б. Закон Ома для резистора имеет вид:
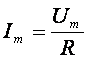 или
или 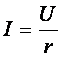 .
.
2.6. Индуктивный элемент в цепи синусоидального тока.
Индуктивный
элемент учитывает явления накапливания
энергии магнитного поля и характеризуется
зависимостью потокосцепления ![]() от
тока
от
тока ![]() :
:
 ,
измеряется в генри (Гн)
,
измеряется в генри (Гн)
. Емкостный элемент в цепи синусоидального тока.
Емкость
отражает явление накапливания энергии
электрического поля и характеризуется
зависимостью заряда ![]() от
напряжения
:
от
напряжения
: 
Аа
Резонансным режимом цепи или просто резонансом называется явление увеличения амплитуды гармонических колебаний энергии в цепи, наблюдаемое при совпадении частоты собственных колебаний o с частотой вынужденных колебаний , сообщаемых цепи источником энергии (o = ). В резонансном режиме колебания энергии между магнитным и электрическим полями замыкаются внутри цепи, обмен энергией между источником и цепью отсутствует, а вся поступающая от источника энергия преобразуется в другие виды, т.е. электрическая цепь по отношению к источнику энергии ведет себя как чисто активное сопротивление R (активная проводимость G). На этом основании условие для резонансного режима можно сформулировать через параметры элементов схемы, а именно: входное сопротивление и, соответственно, входная проводимость схемы со стороны выводов источника энергии должна носить чисто активный характер: Zвх=Rвх; Yвх=Gвх; Xвх=0; Bвх=0;
Резонанс в последовательном контуре
Рассмотрим простейший колебательный контур (рис. 2.23). Комплексное сопротивление цепи
Рис. 2.23. RLC колебательный контур Резонанс
наступает при Напряжения
на индуктивности и емкости при этом
оказываются равными друг другу по
величине (UL =
XLI
= UC =
XCI)
и скомпенсированными друг с другом.
Приложенное напряжение падает только
на активном сопротивлении. Полное
сопротивление Z при X = 0 будет равно Условие равенства ωL = 1/ωC показывает, что в общем случае резонансных условий можно достичь, изменяя или параметры цепи L и C или частоту питания ω. Угловая частота
называется резонансной угловой частотой. Сопротивление
называется характеристическим или волновым. |
Резонансными кривыми называются зависимости тока и напряжения от частоты.
добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению:
|
в электрических цепях синусоидального тока возможно возникновение взаимной индукции. Физически это можно объяснить так: изменение тока в одной цепи вызывает изменение величины потокосцепления взаимной индукции в другой и наоборот. В данном случае говорят, что эти цепи индуктивно связаны.
Для выяснения явлений в индуктивно связанных цепях рассмотрим две катушки (рис. 6.1). Пусть, например, в катушке 1 протекает ток i1, а во второй ток отсутствует. Тогда i1 вызывает магнитный поток Ф11, который пронизывает все витки первой катушки и вызывает ЭДС самоиндукции. Поскольку катушки находятся достаточно близко друг от друга, то часть силовых линий Ф11 пронизывает витки второй катушки, где Ф21 – это часть Ф11, пронизывающая катушку 2. Трехфазные цепи Расчет электрических цепей
Ф11 > Ф21;
11 = W1 Ф11 – потокосцепление первой катушки;
21 = W2 Ф21 – потокосцепление второй катушки.
Поделим оба выражения на i1
![]() ;
; ![]()
![]() . 115(6.1)
. 115(6.1)
Аналогичная картина могла бы иметь место при протекании тока во второй катушке:
![]() ;
;
![]() . 116(6.2)
. 116(6.2)
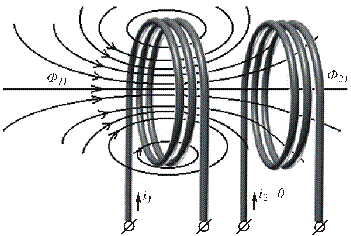
Рис.6.1. Индуктивно связанные катушки
Однако поскольку магнитные свойства среды, заполняющей катушки (воздух), неизменны, то M12 = M21 = M – взаимная индуктивность двух катушек (индуктивная связь) – величина неизменная и зависит только от взаимного положения и чисел катушек. Степень индуктивной связи характеризуется коэффициентом связи
![]() 117(6.3)
117(6.3)
В зависимости от нагрузки различают следующие режимы работы: номинальный, режим холостого хода, короткого замыкания, согласованный режим. При номинальном режиме электротехнические устройства работают в условиях, указанных в паспортных данных завода-изготовителя. В нормальных условиях величины тока, напряжения, мощности не превышают указанных значений.
Трансформатором называют статический электромагнитный аппарат, предназначенный для преобразования переменного тока одного напряжения в переменный ток другого напряжения.
Коэффициент трансформации – это отношение ЭДС обмоток, равное отношению чисел витков обмоток. Приблизительно можно считать коэффициент трансформации равным отношению действующих значений напряжений обмоток:
![]() или
или ![]() ,
,
где Е1 и Е2 – действующие значения ЭДС первичной и вторичной обмоток;
w1 и w2 – числа витков первичной и вторичной обмоток;
Фm – амплитудное значение магнитного потока.
Основных уравнений трансформатора три: уравнение электрического состояния первичной обмотки, уравнение электрического состояния вторичной обмотки и уравнение токов.
Уравнение электрического состояния первичной обмотки:
![]() ,
,
где U1 – комплекс напряжения на первичной обмотке;
Е1 – комплекс ЭДС первичной обмотки;
I1 – комплекс тока первичной обмотки;
r1 – резистивное сопротивление первичной обмотки;
X1 – индуктивное сопротивление рассеивания первичной обмотки.
Уравнение электрического состояния вторичной обмотки:
![]() ,
,
где U2 – комплекс напряжения на вторичной обмотке;
Е2 – комплекс ЭДС вторичной обмотки;
I2 – комплекс тока вторичной обмотки;
r2 – резистивное сопротивление вторичной обмотки;
X2 – индуктивное сопротивление рассеивания вторичной обмотки.
Уравнение токов:
![]() ,
,
где Ix – ток холостого хода трансформатора.
Трехфазной называется электрическая цепь, в ветвях которой действуют три одинаковые по амплитуде синусоидальные ЭДС, имеющие одну и ту же частоту, сдвинутые по фазе одна относительно другой на угол 2π/3 (120°)
1 Симметричные системы линейных и фазных токов и напряжений содержат составляющие только прямой последовательности.
2. Ток в нейтральном проводе равен утроенному значению тока нулевой последовательности:
![]() ;
;
![]() ,
,
следовательно, ![]() .
.
3. В трехпроводной системе отсутствуют линейные токи нулевой последовательности:
![]() .
.
4.
Система линейных напряжений не содержит
составляющей нулевой последовательности,
так как сумма линейных напряжений всегда
равна нулю. Степень несимметрии линейных
напряжений оценивается коэффициентом
несимметрии e, представляющим отношение
составляющей обратной последовательности
к составляющей прямой ![]() .
.
5. Фазные напряжения симметричного приемника, соединенного «звездой», при несимметричных линейных напряжениях не содержат составляющих нулевой последовательности. Как было показано ранее
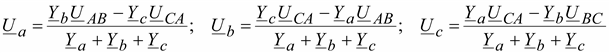 .
.
При ![]()
![]() .
.
Тогда ![]() .
.
6.
Симметричные составляющие нулевой
последовательности фазных напряжений
несимметричного приемника при несимметрии
линейных напряжений равны напряжению ![]() между
нейтральными точками N и n симметричного
и несимметричного приемников.
между
нейтральными точками N и n симметричного
и несимметричного приемников.

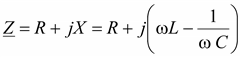 .
(2.35)
.
(2.35)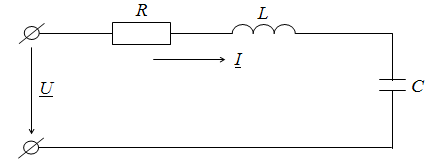
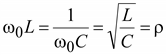 (2.37)
(2.37)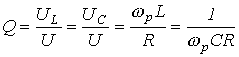 ,
,