1. Электрической цепью называется совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электрическом токе, ЭДС (электродвижущая сила) и электрическом напряжении.

Для анализа и расчета электрическая цепь графически представляется в виде электрической схемы, содержащей условные обозначения ее элементов и способы их соединения.

Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов.

Узел электрической цепи (схемы) – место соединения трех и более ветвей.

Контур – любой замкнутый путь, проходящий по нескольким ветвям.

Элемент электрической цепи, параметры которого не зависят от тока в нем, называют линейным

Направление: для токов в ветвях, содержащих источники ЭДС – совпадающими с направлением ЭДС; во всех других ветвях произвольно; для напряжений – совпадающими с направлением тока в ветви или элемента цепи.

2. схема замещения источника энергии содержит два элемента. В зависимости от используемых элементов источник энергии может быть представлен последовательной или параллельной схемой замещения, которые эквивалентны между собой. последовательная (а) и параллельная (б) схемы замещения линейного источника

.

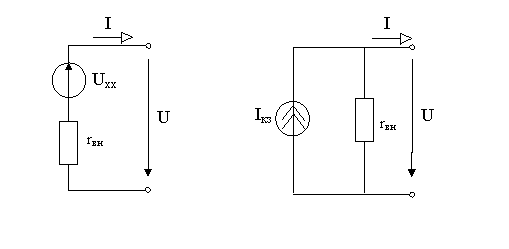
У идеального источника ЭДС внутреннее сопротивление r₀<<R_н (приближенно r₀≈0). В этом случае его вольт-амперная характеристика представляет собой прямую линию, следовательно, напряжение U на его зажимах постоянно (U=E) и не зависит от величины сопротивления нагрузки R_н.

В идеальном источнике тока r₀>>R_н. В этом случае можно считать, что при изменении сопротивления нагрузки R_н потребителя I₀≈0, аI≈I_к. Тогда следует, что вольт-амперная характеристика I(U) идеального источника тока представляет прямую линию, проведенную параллельно оси абсцисс на уровне I=I_к=E/r₀

3. Первый закон Кирхгофа

В любом узле электрической цепи алгебраическая сумма токов равна нулю

,

где m – число ветвей подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус».

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках

,

где n – число источников ЭДС в контуре; m – число элементов с сопротивлением R_k в контуре; U_k=R_kI_k – напряжение или падение напряжения на k-м элементе контура.

При записи уравнений по второму закону Кирхгофа необходимо:

1) задать условные положительные направления ЭДС, токов и напряжений;

2) выбрать направление обхода контура, для которого записывается уравнение;

3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

Запишем уравнения по II закону Кирхгофа для контуров электрической схемы

контур I: E=RI+R₁I₁+r₀I,

контур II: R₁I₁+R₂I₂=0,

контур III: E=RI+R₂I₂+r₀I.

4. Метод контурных токов

В методе контурных токов за основные неизвестные величины принимают контурные токи, которые замыкаются только по независимым контурам (главным контурам). Контурные токи находят, решая систему уравнений, составленную по второму закону Кирхгофа для каждого контура. По найденным контурным токам определяют токи ветвей схемы.

Алгоритмом метода контурных токов:

1. Задаются направлением токов ветвей и обозначают их на схеме.

2. Определяют независимые контуры и их нумеруют. При наличии в схеме источников тока независимые контуры, для которых составляются уравнения метода контурных токов, можно определить, если мысленно удалить источники тока.

3. Выбирают направление контурных токов (целесообразно в одну сторону) и составляют уравнения по методу контурных токов, обходя каждый контур в направлении его контурного тока. Контурный ток, проходящий через источник тока, известен и равен току источника тока (через источник тока проходит только один контурный ток!).

4. Полученную систему алгебраических уравнений решают относительно неизвестных контурных токов.

5. Искомые токи по методу контурных токов находят как алгебраическую сумму контурных токов, проходящих по данной ветви. Токи в ветвях связи равны контурным токам.

5. Метод узловы́х потенциалов — метод расчета электрических цепей путем записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.

Методика

1. Записывают уравнения для токов в ветвях схемы по обобщенному закону Ома.

2. Записывают для всех узлов, кроме одного, уравнения по 1 закону Кирхгофа.

3. В уравнения 1-ого закона Кирхгофа подставляют токи из уравнений обобщенного закона Ома, раскрывают скобки и проводят подобие относительно потенциалов узлов.

.

6. В любой электрической цепи сумма мощностей всех источников электрической энергии должна быть равна сумме мощностей всех приемников и вспомогательных элементов. 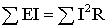называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение EI подставляют в со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение EI подставляют в со знаком минус.

7. Принцип наложения: ток (напряжение) на участке цепи, в которой действуют несколько независимых источников ЭДС и тока, равен алгебраической сумме токов (напряжений), вызываемых каждым из этих источников в отдельности. Принцип базируется на линейности уравнений цепи и позволяет свести задачу анализа цепи к рассмотрению частных режимов, в каждом из которых учитывается один независимый источник. Управляемые источники, действующие в цепи, следует учитывать в каждом из частных режимов.

Принцип взаимности определяет связи между токами и напряжениями в двух ветвях пассивной цепи при действии в них источников различного характера

Принцип компенсации основан на теореме о компенсации, которая гласит: в любой электрической цепи без изменения токов в ее ветвях сопротивление в произвольной ветви можно заменить источником с ЭДС, численно равной падению напряжения на этом сопротивлении и действующей навстречу току в этой ветви.