Показники варіації, асиметрії та ексцесу дискретного та інтервального ряду.

Показники варіації кількісних ознак

Найпростішою мірою варіації кількісної ознаки в сукупності є розмах варіації:

Розмах варіації є абсолютним показником і має ту ж одиницю виміру, що і значення варіюючої ознаки. Для порівняння варіації ознаки у двох сукупностях застосовують відносні показники варіації (абсолютні, ділені на середню арифметичну). Відносний показник варіації, розрахований на основі розмаху варіації, називають коефіцієнтом осциляції:

Перевагою розмаху варіації є її простота та наочність. Проте їхнє значення базується на двох крайніх значеннях ознаки і не показує варіацію між цими крайніми значеннями. Тому більш поширеними є показники варіації, що охоплюють кожне значення варію­ючої ознаки:

1) середнє лінійне відхилення:

для незгрупованих даних

для згрупованих даних

2) відносне лінійне відхилення:

3) середнє квадратичне відхилення:

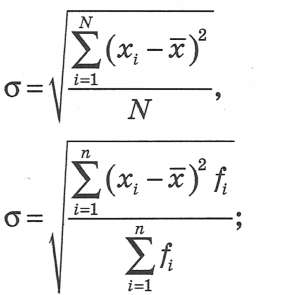
відповідно для не згрупованих та згрупованих даних

4) дисперсія

для не незгрупованих даних

для згрупованих даних

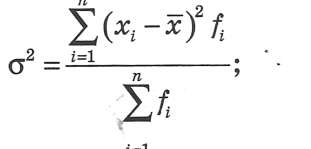
5) коефіцієнт варіації (відносне квадратичне відхилення):

Найчастіше для оцінки ступеня варіації використовують коефіцієнт варіації:

-V < 10 % вказує на незначну варіацію;

-10 % < V < 30 % вказує на посередню варіацію;

-V > 30 % вказує на значну варіацію(розподіл сукупності неоднорідний)

Асиметрія

Скошеність ряду розподілу від центра праворуч (ліворуч) характеризує асиметрія. Її відносний показник оцінюють порівнянням середніх показ­ників:

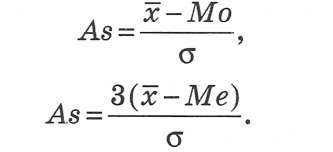
Величина цього коефіцієнта може бути додатною та від'ємною. У випад­ку Аз > 0 маємо справу із правобічною асиметрією (див. Рис 2.1.2), у випад­ку Аз < 0 — із лівобічною (див. рис. 2.1.3).

Для аналізу асиметрії ряду розподілу найчастіше використовують стан­дартизований момент третього порядку:

Ексцес

Міра ексцесу — це крутизна розподілу залежно від варіації ознаки. Її визначають для симетричних та помірно асиметричних розподілів:

Залежно від знака величини ексцесу розрізняють гостровершинний та плосковершинний розподіли (рис. 3.4.). Застосування коефіцієнта асиметрії дозволяє оцінити ступінь асиметрії: вважають, якщо Аs > ±0,25, то асиметрія є незначною, а якщо Аs > ±0,5, то асиметрія значна.

Рис. 3.4. Форми розподілу

Елементи Microsoft Excel для розрахунку моди, медіани, середнього значення, варіації, асиметрії та ексцесу часового ряду.

Формула INDEX повертає значення або посилання на значення з таблиці або інтервалу. Функція INDEX має дві синтаксичні форми: масив і посилання:

INDEX (масив;номер_рядка;номер_стовпця) повертає значення вказаної клітинки або масив клітинок в аргументі «масив»,

INDEX (гюсилання;номер рядка;номер_стовпця;номер_області) повертає посилання на вказані клітинки в аргументі «посилання». При розв'язанні задачі використано другу форму цієї формули.

1. INDEX/IHДЕКС (посилання;номер_рядка;номер__стовпця;н омер_області)

• посилання - це посилання на один або декілька діапазонів клітинок. Якщо несуміжний діапазон використовується як посилання, аргумент «посилання» потрібно взяти в дужки. Якщо кожна область в посиланні містить лише один рядок або стовпець, то аргумент номер_рядка або иомер__стовпця, відповідно, не є обов'язковим. Наприклад, для посилання з одним рядком слід використовувати форму INDEX(посилаиня;;иомер_стовпця).

• номер_рядка - це номер рядка в . аргументі «посилання», з якого

потрібно повернути посилання.

• Номер_стовпця - це номер стовпця в аргументі «посилання», з якого потрібно повернути посилання.

• Номер_області - це діапазон в аргументі «посилання», з якого потрібно повернути перетин номер-рядка та номер_стовпця. Перші виділена або введена область — область 1, друга - область 2 і т. д Якщо номер області пропущено, то функція INDEX використовує область 1.

• Якщо встановити номер_рядка або номер_стовпця рівним 0 (нулю) та функція INDEX поверне масив значень для цілого стовпця або рядка відповідно. Для використання масиву значень введіть функцію INDEX я формулу масиву, в горизонтальний діапазон клітинок для рядка та у вертикальний — для стовпця. Щоб ввести формулу масиву, натиснувши клавіші CTRL+SHIFT+ENTER.

• Номер рядка та номер_стовпця мають указувати на клітинку і масиві; в іншому випадку функція INDEX повертає значення помилки #REF!

2. MATCH/ПОИСКПОЗ(шукане_значення;масив_перегляду;тип_співпадіння) повертає відносне розташування елемента масиву, який відповідає вказаному значенню в указаному порядку. Функція МАТСН використовується замість однієї: функцій LOOKUP, коли потрібно визначити розташуванню елемента в діапазоні, а не сам елемент.

• шукане_значення - це значення, яке використовується для пошуку значень у таблиці.

• Шукане_значення - це значення, яке зіставляється зі значеннями аргументу мас|в_перегляду.

• шукаие_значення може бути значенням (числом, текстом або логічним значенням) або посиланням на клітинку, яка містити число, текст або логічне значення.

• масив_перегляду - це безперервний інтервал клітинок, які містять можливі шукані значення. Масив_перегляду може бути масивом або посиланням на масив.

• тип_співпадіння - це число -1,0 або 1. Тип_співпадіння вказує, як Microsoft Excel зіставляє шукане_значення зі значеннями аргументу масив_перегляду.

Якщо тип_співпадіння дорівнює 1 то функція МАТСН знаходить найбільше значення, яке не перевищує шукане_значення. Значення в аргументі масив_перегляду повинні розташовуватися за зростанням: 2, -1, 0,1,2, A-Z, FALSE_TRUE/

Якщо тип_співпадіння дорівнює О, то функція МАТСН знаходить перше значення, яке точно дорівнює аргументу шукаие_значення. Порядок елементів у масиві_перегляду може бути довільним. Якщо тип_співпадіння дорівнює -1, то функція МАТСН знаходить найменше значення, не менше за шукане_значення. Значення в аргументі масив_перегляду повинні розташовуватися за спаданням: TRUE, FALSE, 2-А, ...2,1, 0, -1, -2, і т. д.

Якщо аргумент тип_співпадіння пропущено, приймається значення 1.

3. SUMMPRODUCT/СУММПРОИЗВ(масив 1 ;масив2;масивЗ; ...) Перемножує відповідні компоненти вказаних масивів і повертає суму добутків ® масиві, масив2, масивЗ, ... - це від 2 до 30 масивів, компоненти яких потрібно перемножити, а потім додати.

4. LEFT/ЛЕБСИМ (текст;кількість_зиаків) повертає перші знаки текстового рядка, виходячи з указаної кількості знаків.

5. RIGHT/ПРАВСИМ(текст;кількість_знаків) повертає вказану кількість останніх знаків текстового рядка

6. ABS(число) повертає модуль (абсолютне значення) числа.

7. SQRT/КОРЕНЬ (число) повертає додатне значення квадратного кореня.

8. POWER/СТЕПЕНЬ(число;степінь) повертає результат піднесення числа до степеня.

Розрахунок моди, медіани, показників варіації, асиметрії та ексцесу інтервального ряду

Відповідно до набутих теоретичних знань було проведено обчислення основних показників статистичних рядів. У результаті обчислень було отримано наступні результати (Табл. 3.2 – 3.6).

Таблиця 3.2

Розмах варіації інтервального ряду

Розмах варіації
Показник	Результат
Розмах варіації	351,15

Таблиця 3.3

Мода інтервального ряду

Середні величини
Мода
Показник	Результат
Найбільша частота	120
Модальний інтервал	143,33-208,33
Нижня межа модального інтервалу	27,02
Ширина модального інтервалу	13
Частота модального інтервалу	120
Частота передмодального інтервалу	117
Частота післямодального інтервалу	120
Мода	40,02

Таблиця 3.4

Медіана інтервального ряду

Медіана
Показник	Результат
Половина обсягу сукупності	358
Перша комулятивна частота, що перевищує половину обсягу сукупності	477
Медіальний інтервал	143,33-208,33
Нижня межа медіального інтервалу	143,33
Ширина медіального інтервалу	65
Комулятивна частота домедіального інтервалу	357
Частота медіального інтервалу	120
Медіана	143,8716667

Таблиця 3.5

Показники варіації інтеравального ряду

Показники варіації
Показники варіації	Результат
Середня арифметична	162,34
Середнє лінійне відхилення	125,84
Дисперсія	18495,58
Середнє квадратичне відхилення	136,00
Відносне лінійне відхилення	77,52
Коефіцієнт варіації	83,77
Оцінка варіації	варіація значна
Оцінка однорідності розподілу	розподіл сукупності неоднорідний

Таблиця 3.6

Асиметрія та ексцес інтервального ряду

Асиметрія та ексцес
Показник	Результат
Середня арифметична	162,3397765
Відхилення	103,1356596
Порядку	389381,3624
Коефіцієнт асиметрії	0,354934821
Оцінка асиметрії	правостороння
оцінка ступеня асиметрії	асиметрія помітна
Обсяг сукупності	1432
Середньоквадратична похибка асиметрії	0,064616941
Оцінка асиметрії генералльної сукупності	розподіл генеральної сукупності несиметричний
Центральний момент 4-го порядку	2565438,817
Ексцес	-2,977326098
Оцінка ексцесу	плосковершинний