3. Формули для розрахунку та розрахунок розмаху варіації, середніх величини, оцінки варіації за допомогою редактора формул

Поняття моди, медіани та середнього значення дискретного та інтервального ряду.

Аналіз результатів спостереження та зведення у статистиці передбачає розрахунок такого узагальнюючого показника, який би характеризував усю сукупність явищ. Таку функцію виконують середні величини. Залеж­но від мети дослідження, характеру сукупності та виду варіюючих ознак у статистиці використовують різні види середніх величин. їх поділяють на центральні (степеневі) та порядкові (структурні).

Мода

Мода — це значення ознаки, що трапляється в сукупності найчастіше. Моду атрибутивного та дискретного рядів розподілу визначають за алгоритмом:

Крок 1. Визначають найбільшу частоту (частку) розподілу.

Крок 2. Визначають варіант із найбільшою частотою (часткою).

Виходячи з цього алгоритму, моду дискретного ряду розподілу визна­чають за формулою:

Мо = х_{max f}

де x_{max f} - варіант із найбільшою частотою.

Для визначення моди інтервального ряду важливо визначити, рівними чи нерівними є його інтервали. Якщо нерівні — моду визначають за щільностями, а не за частотами (частками) (табл. 3.1)

Таблиця 3.1.

Визначення моди інтервального ряду

Медіана

Медіана — це значення ознаки, що поділяє упорядковану за зростанням чи спаданням сукупність на дві рівні частини. Одна частина сукупності за значенням менша за медіану, друга — більша.

Для визначення медіани незгрупованих даних їх насамперед упорядко­вують за зростанням чи спаданням(ранжують). Ранг медіани у цій упоряд­кованій сукупності залежить від того, парним чи непарним числом є обсяг сукупності:

N — парне

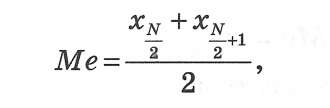
N — непарне

де N — обсяг одиниць сукупності ряду розподілу.

В інтервальному ряді розподілу медіану визначають так:

Крок 1. Визначають половину обсягу сукупності (N/2).

Крок 2. Визначають кумулятивну частоту, яка першою більша або до­рівнює половині обсягу сукупності.

Крок 3. Якщо ряд розподілу дискретний — варіант, що відповідає знайденій у пункті 2 кумулятивній частоті, і є медіаною; якщо інтервальний — цій кумулятивній частоті відповідає медіан­ний інтервал.

Крок 4. Визначають медіану за формулою:

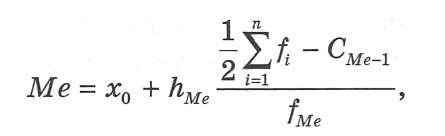
де х₀ — нижня межа медіанного інтервалу; C_Ме — ширина медіанного інтервалу; С_Ме-₁ — сума частот (або часток) усіх домедіанних інтервалів (кумулятивна частота передмедіанного інтервалу); f_Ме — частота медіанного інтервалу.

Оцінка форми розподілу на основі порівняння середніх

Порівняння середніх показників сукупності (моди, медіани та серед­нього арифметичного) дає уявлення про її форму розподілу. Так, якщо значення названих середніх збігається, є підстави стверджу­вати, що розподіл симетричний (рис. 3.1).

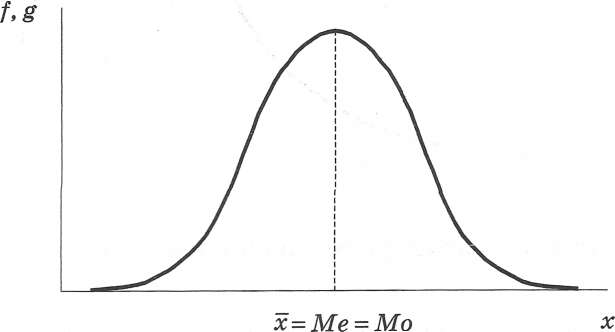
Рис. 3.1. Симетричний розподіл, асиметрія відсутня

Якщо в сукупності є декілька аномально великих(порівняно з усією сукупністю) значень, середня арифметична завжди матиме більші значення, ніж мода та медіана. Пояснюється це тим, що мода та медіана нечутливі до крайніх(аномальних) значень сукупності. Натомість для розрахунку середньої враховують усі значення сукупності, у тому числі аномальні. Аномально великі значення ознаки формують додатну (правобічну) аси­метрію (рис. 3.2).

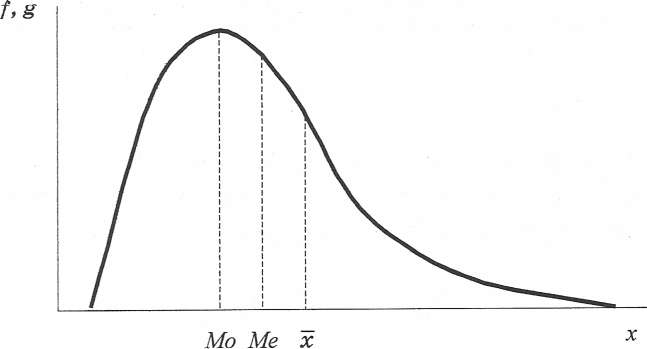
Рис. 3.2. Розподіл з додатною (правобічною) асиметрією

Аномально малі значення сукупності, навпаки, зменшують середню арифметичну порівняно з модою та медіаною. Тут маємо справу з від'ємною (лівобічною) асиметрією (рис.3.3.)

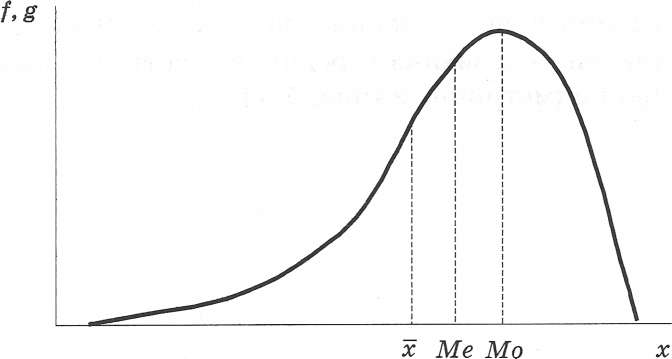
Рис.3.3. Розподіл з від'ємною (лівобічною) асиметрією