2. Довірчий інтервал і довірча імовірність.

Вище був розглянутий спосіб одержання точкових оцінок для математичного сподівання і дисперсії.

Однак, при вибірці малого обсягу точкова оцінка може значно відрізнятися від параметра який оцінюється і, отже, приводити до грубих помилок.

Більш повний і надійний спосіб оцінювання параметрів випадкових

величин полягає у визначенні інтервалу (а не єдиного точкового значення), в якому із заданим ступенем вірогідності буде укладене значення параметра, який оцінюється.

Такого роду оцінки називаються інтервальними оцінками, що особливо важливо при малому числі спостережень.

Інтервальною називають оцінку, яка визначається двома числами - кінцями інтервалу. Інтервальні оцінки дозволяють встановити точність і надійність оцінок.

Задача інтервального оцінювання може бути сформульована таким чином. За даними, отриманими в результаті дослідів, необхідно побудувати інтервал І_ (рис. 3.1), щодо якого з заздалегідь обраною імовірністю  можна сказати, що він накриє справжнє значення параметра а, який оцінюється.

Р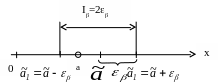 ис. 3.1

Нехай для параметра а отримана з досліду незміщена оцінка . Будемо вважати параметр а постійним числом (хоча а може бути і випадковою величиною). Ясно, що оцінка тим точніше визначає параметр а, чим менше абсолютна величина різниці | - а|. Іншими словами, якщо _  0 і | - а|  _, то чим менше _, тим оцінка точніше. Таким чином, позитивне число _ характеризує точність оцінки (рис. 3.1).

Однак статистичні методи не дозволяють категорично стверджувати, що оцінка задовольняє нерівності | - а|  _ , можна лише говорити про імовірність , з якою ця нерівність здійснюється.

Імовірність  називають довірчою імовірністю (надійністю, або коефіцієнтом довіри). Власно кажучи довірча імовірність , яка відповідає даному довірчому інтервалу І_, - це імовірність того, що справжнє значення параметра, який оцінюється, знаходиться в цьому інтервалі. Звичайно довірча імовірність  задається наперед, причому в якості  беруть досить велику імовірність, рівну (0,90  0,98), таку, щоб подію з імовірністю  можна було вважати практично достовірною, і знаходять таке значення _  0, для якого

Р(| - а|  _) =  . (3.19)

Тоді діапазон практично можливих помилок, що виникають при заміні а на буде  _ ; великі по абсолютній величині помилки будуть з'являтися з дуже малою імовірністю   .

Наприклад, якщо обрано довірчу імовірність = 0,98, то це значить, що в 98% побудований нами за результатами іспитів довірчий інтервал з випадковими границями оцінюваного параметра а і лише в 2 % містити його не буде.

Замінивши нерівність | - а|  _ рівносильною йому подвійною нерівністю - _  - а  _ або , маємо

_{. (3.20)}

Це співвідношення варто розуміти так: імовірність того, що інтервал ( - _,, + _ ) укладає в собі (покриває) невідомий параметр а, дорівнює .

Числа називають довірчими границями інтервалу І_. Вони є випадковими величинами і можуть бути як симетричними (  _ ), так і не симетричними.

Підкреслимо, що в теорії імовірностей визначалася імовірність влучення випадкової величини в заданий не випадковий інтервал. У даному випадку випадковою величиною є не оцінюваний параметр а, а довірчий інтервал І_ = 2 _,, і більш правильно говорити не про імовірності влучення крапки а у довірчий інтервал, а про імовірність того, що випадковий інтервал І_ покриє (накриє) крапку а.

Отже, довірчим інтервалом називається інтервал

І_ = ( - _ ; + _), що може накрити не випадковий (хоча і невідомий) параметр а із заданою імовірністю . Довірчий інтервал І_ характеризує точність оцінки. Чим менше І_ при заданій , тим точніше оцінка.

Довірча імовірність характеризує надійність оцінки. Чим більше довірча імовірність при заданому І_ , тим надійніше оцінка.

Метод довірчих інтервалів розробив американський статистик Ю. Нейман, виходячи з ідей англійського статистика Р. Фишера.

Очевидно, що довірчий інтервал, довірча імовірність і обсяг вибірки зв'язані один з одним функціонально. Так, при постійному обсязі вибірки n, зі збільшенням  розширюється довірчий інтервал І_.. Таким чином, при фіксованому обсязі вибірки неможливо для даної оцінки збільшити , не збільшуючи при цьому і довжину І_ .

Для спроможних оцінок при заданій довірчій імовірності  довжина довірчого інтервалу зменшується, прагнучи до нуля, лише зі збільшенням обсягу вибірки до нескінченності.

У загальному випадку при використанні інтервального оцінювання можливі три види задач:

1) задані  і n, визначити І_ ;

2) задані І_ і n, визначити ;

3) задані  і І_ , визначити обсяг вибірки n, для якого одночасно досягаються задані  і І_ .