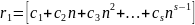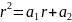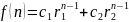- •Рекуррентные соотношения.
- •Доказательство
- •Правила решений рекурсивных соотношений вида (2)
- •Числа Стирлинга
- •Рекуррентные соотношения для чисел Стирлинга второго рода
- •Принцип включения-исключения
- •Задача о беспорядках (как пример метода включений/исключений)
- •Математическая логика Понятия о булевых функциях
- •Свойства n-местных булевых функций
- •Булева алгебра.
Рекуррентные соотношения.
Некоторые члены последовательности исходя из значений одного или нескольких членов. В задачах комбинаторики это означает уменьшение количества аргументов.
Вычислительное соотношения имеют порядок K, если оно позволяет выразить функцию дискретного аргумента.
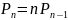
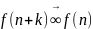
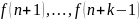
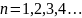
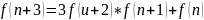
Если задано рекурсивное соотношение k-го порядка, то ему отвечает бесконечно много различных последовательностей.
Рекурсивные соотношения (РС) определяют последовательность только в том случае, если заданы k-первых членов этой последовательности.
Если при подстановке любого члена последовательности рекуррентное соотношение обращается в множество, то мы будем говорить, что эта последовательность является решением данного рекурсивного соотношения.
Пример:
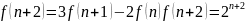
Решением
этого соотношения будет
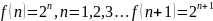
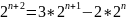
Решением рекуррентного соотношения будем называть общем, если оно зависит от k произвольных постоянных

Путем подбора которых можно получить решение данного соотношения.
Общего правила для решения рекуррентных соотношений не имеется.
Рассмотрим рекуррентное соотношение k-го порядка вида:
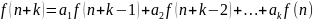 ,
где
,
где
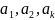 некоторые
числа.
некоторые
числа.
Рекуррентное соотношение вида (1) называется линейным рекуррентным соотношением с постоянными коэффициентами.
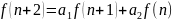 – второй порядок
– второй порядок
Пусть
известны
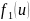 и
и
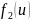 (2), отсюда вытекает следующее утверждение:
(2), отсюда вытекает следующее утверждение:
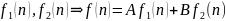
Для
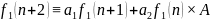
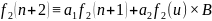
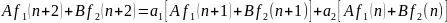
Таким
образом получили второе тождество;
следовательно
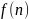 обращает выражение (2) в тождество и
является решение рекуррентного
соотношения.
обращает выражение (2) в тождество и
является решение рекуррентного
соотношения.
Запишем следующее квадратное уравнение соответственно по отношению ко (2)
Это уравнение назовем характеристическим уравнением для (2)
Пусть
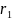 корень, тогда запишем утверждение (2):
корень, тогда запишем утверждение (2):
Утверждение
(2): Последовательность
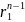 ,
где n = 1,2,3… также является
решением соотношения (2), таким образом:
,
где n = 1,2,3… также является
решением соотношения (2), таким образом:
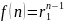 ,
,
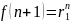 ,
,
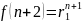 ,
тогда подставив эти значения в уравнение
(3) получим
,
тогда подставив эти значения в уравнение
(3) получим
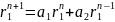 .
Разделим это выражение на
и получим:
.
Разделим это выражение на
и получим:
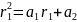 ,
это тождество очевидно, итак
,
это тождество очевидно, итак
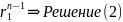
Доказательство
Пусть
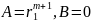
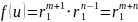 то есть получили аналог
то есть получили аналог
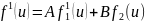
Правила решений рекурсивных соотношений вида (2)
Для
соотношения (2) составленное квадратное
уравнение вида (3) называется
характеристическим, если это уравнение
будет иметь 2 различных корня
и
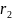 то общее решение (2) будет иметь вид
то общее решение (2) будет иметь вид
Любое
решение рекурсивного соотношения
однозначно определено двумя значениями
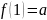
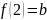 ,
подставим их в уравнение (4) получим:
,
подставим их в уравнение (4) получим:
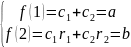 (5)
(5)
Получили линейное уравнение
Общее решение этой системы будет:
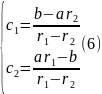
Решение
имеет место для любых a и
b и можно всегда найти
значение
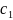 и
и
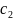 то есть решение всегда есть и имеет
единственное значение в результате его
можно представить в виде уравнения (4)
то есть решение всегда есть и имеет
единственное значение в результате его
можно представить в виде уравнения (4)
Пример:
Пусть дано уравнение
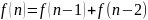 – Рекурсивное соотношение 2-го порядка.
Если положив в это уравнение
– Рекурсивное соотношение 2-го порядка.
Если положив в это уравнение
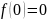 и
и
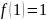 ,
то в результате получим рекурсивное
соотношение которое определяет
последовательность чисел полученных
Фибоначчи.
,
то в результате получим рекурсивное
соотношение которое определяет
последовательность чисел полученных
Фибоначчи.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 59, 144, 233.
Эта последовательность используется при кодировании информации.
Характеристическое уравнение для этой последовательности чисел будет:
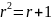 ,
где
,
где
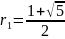 ,
а
,
а
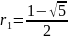
Общее
решение:
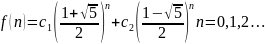
Требуется
найти значения
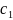 и
и
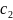 соответственно заданным начальным
требованиям:
соответственно заданным начальным
требованиям:
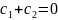
Берем n = 1

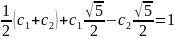
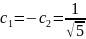
Итак, общее решение будет иметь вид (числа Фибоначчи):
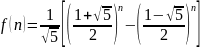
Пусть корни
уравнения будут равные, то есть
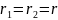 (корень кратный)
(корень кратный)
(7)
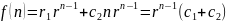 и далее по аналогии.
и далее по аналогии.
Если имеется
рекурсивное соотношение k-го
порядка вида (1)
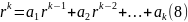
Если корни этого характеристического уравнения будут различны, то общее решение его будет:
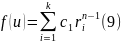
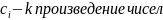
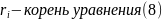
Пример:
Пусть
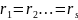 этому корню кратности s
в выражении (9) будет соответствовать
своя сумма в выражении для общего решения
уравнения
этому корню кратности s
в выражении (9) будет соответствовать
своя сумма в выражении для общего решения
уравнения