
- •§19. Теорема о движении центра масс.
- •§20. Момент силы
- •§21. Момент импульса.
- •§22. Уравнение моментов.
- •§23. Закон сохранения момента импульса.
- •§24. Момент импульса твердого тела. Понятие тензоре инерции. Главные оси инерции.
- •§25. Вращение твердого тела вокруг неподвижной оси.
- •§26. Момент инерции твердого тела относительно оси.
- •§27. Кинетическая энергия твердого тела
- •§28. Работа внешних сил при вращении тела вокруг неподвижной оси
- •§29. Гироскопы
§19. Теорема о движении центра масс.
Ранее мы рассмотрели динамику движения материальной точки. Теперь наша задача состоит в том, чтобы определить, как будет двигаться тело под действием произвольно приложенных сил.
Если в результате действия на тело всех сил оно движется поступательно, то расчет движения производится так же, как и для материальной точки, предполагая, что все силы приложены к центру масс тела.
Если в результате действия всех сил тело движется сложным образом, и все точки тела имеют разные скорости и ускорения, то в этом случае движение тела можно представить как сумму поступательного и вращательного движений. При этом за поступательное движение тела принимают движение некоторой, причем любой, точки, жестко связанной с самим телом. Эту точку называют полюсом, и затем рассматривают вращательное движение тела вокруг этого полюса.
Если нам заранее ничего не известно о движении тела, то какую точку надо принять за полюс? Ведь без этого мы не сможем представить движение тела как сумму поступательного и вращательного движений.
Давайте ответим на этот вопрос.
Допустим, под действием некоторых внешних сил Fi тело массой М, вращаясь, перемещается в пространстве. Мысленно разобьем все тело на материальные точки mi. Затем воспользуемся выражением (18.2), отражающим связь между изменением импульса системы материальных точек и суммой внешних сил, действующих на эту систему.
![]() .
(19.1)
.
(19.1)
Сумма
![]() представляет собой сумму всех действующих
на тело сил, и если они известны, то ее
вычисление не представляет трудностей.
Что же представляет собой сумма
представляет собой сумму всех действующих
на тело сил, и если они известны, то ее
вычисление не представляет трудностей.
Что же представляет собой сумма![]() ?
Эта сумма уже входила в выражение (18.7)
для ускорения центра масс. Следовательно,
сумма
?
Эта сумма уже входила в выражение (18.7)
для ускорения центра масс. Следовательно,
сумма![]() равна
равна![]() и, подставив это значение суммы в
уравнение (19.1), получим:
и, подставив это значение суммы в
уравнение (19.1), получим:
![]() .
(19.2)
.
(19.2)
Итак, под действием произвольно приложенных сил тело сложным образом меняет свое положение в пространстве. При этом кинематические параметры всех точек тела отличаются друг от друга, но движение одной точки можно описать сразу. Эта точка – центр инерции!
Центр инерции тела движется так, как двигалась бы материальная точка массой М, равной массе твердого тела, под действием всех приложенных к телу сил.
Этот результат называют теоремой о движении центра масс.
Поэтому чаще всего центр масс принимают за полюс, а траекторию его движения считают траекторией поступательного движения тела.
§20. Момент силы
В предыдущем параграфе мы выяснили, как можно описать поступательное движение твердого тела, под действием произвольно приложенных к нему сил.
Если бы теперь мы смогли описать вращательное движение твердого тела вокруг центра инерции, то задача описания движения твердого тела под действием произвольных сил была бы выполнена.
Прежде чем приступить к описанию вращательного движения твердого тела, необходимо ввести дополнительные понятия момента силы и момента импульса.
Для того чтобы повернуть тело вокруг точки O, нужно создать вращающий момент, действующий на тело. Эффективность этого вращающего момента N зависит от момента силы, который определяется приложенной силой F и вектором r, соединяющего точку О и точку приложения силы F (рис 20.1).
М оментом
силыNO
относительно точки О называется
векторное произведение вектора r
на вектор силы F.
оментом
силыNO
относительно точки О называется
векторное произведение вектора r
на вектор силы F.
![]() .
(20.1)
.
(20.1)
Момент силы относительно точки – векторная величина, направление которой определяется по правилу «буравчика» (см. рис. 20.1).
Составляющие момента силы вычисляется по определителю (2.17):
N
= =еx
=еx![]() –
–![]()
![]() +еz
+еz![]() .
(20.2)
.
(20.2)
Если вектор NO спроектировать на произвольную ось Z, то эта проекция Nz будет называться моментом силы F относительно оси Z. Момент силы относительно оси – скалярная величина, знак которой зависит от выбранного направления оси Z. Вычислить эту величину можно, рассчитав определитель третьего слагаемого в выражении (20.2).
Если начало системы координат не совпадает с точкой О, то для определения проекций момента импульса на координатные оси можно поступательно сместить систему координат до совмещения начала отсчета с точкой О.
Моментом N нескольких сил относительно точки О называется векторная сумма моментов этих сил относительно той же точки.
![]()
 .
(20.3)
.
(20.3)
Поскольку нам
придется рассматривать движение тела
относительно различных точек, рассмотрим,
как при этом меняется суммарный момент
всех сил (20.3). Пусть
![]() суммарный момент сил относительно точкиО
в данной системе отсчета. Тогда в
этой же системе отсчета суммарный
момент сил относительно другой точки
О¢
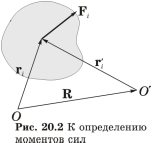
будет равен (см. рис. 20.2):
суммарный момент сил относительно точкиО
в данной системе отсчета. Тогда в
этой же системе отсчета суммарный
момент сил относительно другой точки
О¢
будет равен (см. рис. 20.2):
![]() .
(20.4)
.
(20.4)
В этом выражении:
ri – вектор, проведенный из точки O в точку приложения силы Fi.
r¢i – вектор, проведенный из точки O¢ в точку приложения силы Fi.
R – вектор, проведенный из точки O в точку O¢.
![]() Из
выражения (20.4) следует, что если
сумма всех сил, действующих на тело
Из
выражения (20.4) следует, что если
сумма всех сил, действующих на тело
![]() =0,
то суммарный момент этих сил не зависит
от того, относительно какой точки мы
вычисляем эти моменты.
=0,
то суммарный момент этих сил не зависит
от того, относительно какой точки мы
вычисляем эти моменты.
Это, в частности, выполняется, когда на тело действует только пара сил.
Парой сил называются две силы F1 и F2, равные по модулю, противоположно направленные и не действующие вдоль одной прямой (рис.20.3). Расстояние l между прямыми, вдоль которых действуют силы, называется плечом пары.
Вычислим суммарный момент этих сил, относительно произвольной точки О, используя обозначения, указанные на рис. 20.3.
N = r1 ´ F1 + r2 ´ F2 = – r1 ´ F2 + r2 ´ F2 = (r2 – r1) ´ F2.
Здесь мы учли, что F1 = –F2.
Обозначим через r12 = r2 – r1 вектор, проведенный из точки приложения силы F1 в точку приложения силы F2. Тогда,
N = r12 ´ F2 (20.5)
О тсюда
видно, что суммарныймомент
пары сил не зависит от выбора точки,
относительно которой мы его рассматриваем,
а его модуль определяется произведением
модуля одной из сил на плечо пары.
÷Nê=
Fr12sin(
тсюда
видно, что суммарныймомент
пары сил не зависит от выбора точки,
относительно которой мы его рассматриваем,
а его модуль определяется произведением
модуля одной из сил на плечо пары.
÷Nê=
Fr12sin(![]() )
= Fl.
В частности, суммарный
момент сил взаимодействия равен нулю,
так как плечо
такой пары сил равно нулю.
)
= Fl.
В частности, суммарный
момент сил взаимодействия равен нулю,
так как плечо
такой пары сил равно нулю.
Так как мы должны рассмотреть вращательное движение твердого тела вокруг центра инерции, рассмотрим, каким свойством в Ц-системе обладает суммарный момент действующих сил.
Если точка О, относительно которой мы вычисляем моменты сил, жестко связана с Ц-системой, то есть с системой отсчета в которой центр масс покоится, то в этой системе сумма всех действующих сил равна нулю (см. 19.3).
Следовательно, в Ц-системе суммарный момент всех сил не зависит, от того относительно какой точки мы вычисляем моменты сил.
![]() .
.
Суммарный момент всех сил, действующих на тело, складывается из моментов внешних сил, моментов сил взаимодействия материальных точек, составляющих тело и моментов сил инерции.
Сумма моментов сил взаимодействия (внутренних сил), как было показано, равна нулю.
Покажем, что в Ц-системе суммарный момент поступательных сил инерции всегда равен нулю.
Поступательная сила инерции, действующая на каждую материальную точку равна Fi = –miwC, где wC – ускорение центра инерции в инерциальной системе отсчета. Тогда суммарный момент всех этих сил относительно точки С равен нулю:
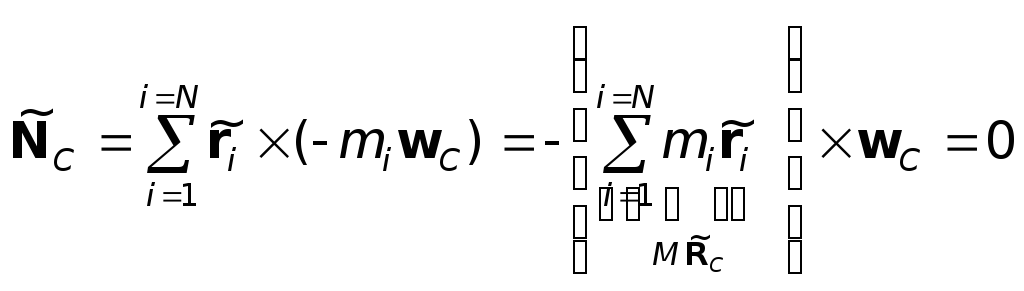 ,
(20.6)
,
(20.6)
так как по условию
![]() = 0.
= 0.
Суммарный момент центробежных сил инерции в Ц-системе в общем случае не равен нулю.
