10. Функциональное отношение. Инъекция, сюръекция, биекция.

Функциональное отношение в теории множеств - это такое бинарное отношение между двумя множествами, при котором каждому элементу первого множества может соответствовать не больше одного элемента второго множества.

Функция называется биекцией (и обозначается ), если она:

Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами,

.

Любой элемент из Y имеет свой прообраз (сюръективность). Иными словами,

.

Биекцию также называют взаимно однозначным отображением (взаимно однозначным соответствием [1]). Множества, для которых существует биекция, называются равномощными.

Отображение называется инъекцией (или вложением, или отображением «в»), если разные элементы множества X переводятся в разные элементы множества Y.

Формально это значит, что если два образа совпадают, то совпадают и прообразы ( ). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).

Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть инъективно, если существует такое, что .

Отображение называется сюръективным (или сюръекцией, или отображением на Y), если каждый элемент множества Y является образом хотя бы одного элемента множества X, то есть . Для случая числовых функций это выражается как «функция, принимающая все возможные значения».

11. В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами). Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах. Граф, или неориентированный граф 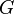  — это упорядоченная пара  , для которой выполнены следующие условия:

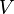•  — это непустое множество вершин или узлов,

•  — это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами. Ориентированный граф (сокращённо орграф)   — это упорядоченная пара  , для которой выполнены следующие условия:

 — это непустое множество вершин или узлов,

•  — это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Смешанный граф   — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой  , где  ,   и   определены так же, как выше.

12. В теории графов дополнением или обратным к графу G называется такой граф H, имеющий то же множество вершин, что и G, но в котором две несовпадающие вершины смежны тогда и только тогда, когда они не смежны в G. Чтобы найти обратный граф, дополните данный граф до полного и удалите все ребра, которые уже были до этого. Пуcть G=(V,E) — простой граф и пусть множество K содержит все двухэлементные подмножества множества V. Тогда H=(V,K\E) является дополнением графа G.

13.  Объединением    графов       и        называется граф  , множество вершин которого есть объединение множеств вершин графов   и  , а множество ребер является объединением множеств ребер  этих графов  .

        Пересечением графов   и   называется граф  , множество вершин которого  , а множество ребер  .

   Кольцевой суммой графов   и   называется граф  , порожденный на множестве ребер  , т. е. на множестве ребер, присутствующих либо в  , либо в  , но не принадлежащих их пересечению 

14. Введем понятие маршрута для графа G = (V, E) (и соответственно понятие пути для орграфа D = (V, E)).

Определение. Маршрутом в данном графе G называется конечная последовательность ребер вида {v0, v1}, {v1,v2}, …, {vm-1, vm} (обозначаемая также v0®v1®v2®…®vm).

Каждому маршруту соответствует последовательность вершин v0v1v2…vm; v0 – начальная вершина, а vm – конечная вершина маршрута. Одна и та же вершина может одновременно оказаться начальной, конечной и внутренней. Таким образом, мы  будем говорить о маршруте из v0 в vm.

Определение. Длиной маршрута называется число ребер в нем.

Определение. Маршрут называется цепью, если все его ребра различны, и простой цепью, если все вершины тоже различны (кроме, может быть, начальной и конечной вершин).

Определение. Цепь или простая цепь замкнуты, если начальная и конечная вершины совпадают.

Определение. Замкнутая простая цепь, содержащая, по крайней мере, одно ребро, называется циклом.

Определение. Обхватом графа называется длина его кратчайшего цикла.

15. Ориентированный граф (кратко орграф) — граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках (Оре) и просто рёбрами. Формально, орграф D=(V, E) есть множество E упорядоченных пар вершин .

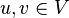Дуга {u, v} инцидентна вершинам u и v. При этом говорят, что u — начальная вершина дуги, а v — конечная вершина.

Орграф, полученный из простого графа ориентацией ребер, называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.

Направленный полный граф называется турниром. Маршрутом в орграфе называют чередующуюся последовательность вершин и дуг, вида (вершины могут повторяться). Длина маршрута — количество дуг в нем.

Путь есть маршрут в орграфе без повторяющихся дуг, простой путь — без повторяющихся вершин. Если существует путь из одной вершины в другую, то вторая вершина достижима из первой.

Контур есть замкнутый путь.

Для полумаршрута снимается ограничение на направление дуг, аналогично определяются полупуть и полуконтур.

Орграф сильно связный, или просто сильный если все его вершины взаимно достижимы; односторонне связный, или просто односторонний если для любых двух вершин, по крайней мере одна достижима из другой; слабо связный, или просто слабый, если при игнорировании направления дуг получается связный (мульти)граф;

Максимальный сильный подграф называется сильной компонентой; односторонняя компонента и слабая компонента определяются аналогично.

Конденсацией орграфа D называют орграф D*, вершинами которого служат сильные компоненты D, а дуга в D* показывает наличие хотя бы одной дуги между вершинами, входящими в соответствующие компоненты.

16. Граф G=(V,E) можно задать списком вершин и ребер. Можно задать и геометрически, нарисовав его на плоскости или любой другой поверхности и отождествив его вершины с точками на плоскости, а ребра с отрезками, соединяющими смежные (соседние) вершины. Определение: Матрица смежности (соседства) вершин (p,q) – графа G=(V,E) с p вершинами есть квадратная симметричная матрица [p x p].

где a_ij: - 1, если вершины V_i,V_j – соседние - 0, в противном случае

Замечание: Всякому графу соответствует его бинарная симметричная матрица смежности. Всякая бинарная симметричная квадратная матрица с нулевой диагональю соответствует некоторому графу.

Определение: Матрица инциденций (соответствий) (p,q) – графа G=(V,E) с p вершинами и q ребрами есть [p x q] матрица

где Bij: 1, если вершина V_i? ребру e_j 0, в противном случае

Замечание: для всякого графа можно построить соответствующую ему бинарную матрицу инциденций.

17. –

18. Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики) от n аргументов — в дискретной математике — отображение Bⁿ → B, где B = {0,1} — булево множество. Элементы булева множества {1, 0} обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определённого смысла. Неотрицательное целое число n называют арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементы декартова произведения (n-я прямая степень) Bⁿ называют булевыми векторами. Множество всех булевых функций от любого числа аргументов часто обозначается P₂, а от n аргументов — P₂(n). Переменные, принимающие значения из булева множества называются булевыми переменными. Булевы функции названы по фамилии математика Джорджа Буля.

При работе с булевыми функциями происходит полное абстрагирование от содержательного смысла, который имелся в виду в алгебре высказываний^[2]. Тем не менее, между булевыми функциями и формулами алгебры высказываний можно установить взаимно-однозначное соответствие, если,

установить взаимно-однозначное соответствие между булевыми переменными и пропозициональными переменными, установить связь между булевыми функциями и логическими связками, оставить расстановку скобок без изменений. Таблица истинности — это таблица, описывающая логическую функцию. Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (true либо false, 1 либо 0). Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.

19. Булевы формулы и называются эквивалентными, если соответствующие им функции и равны.

Обозначение: . Эквивалентные формулы называют также тождественно равными, а выражения вида логическими тождествами . Основные эквивалентности (тождества) Таким образом, эквивалентные формулы являются различными заданиями одной и той же булевой функции. Ниже мы приводим ряд пар эквивалентных формул (тождеств), отражающих существенные свойства логических операций и важные соотношения между различными операциями. Они часто позволяют находить для булевых функций по одним задающим их формулам более простые формулы. Большинство из приводимых тождеств имеют собственные имена. Часто их называют законами логики.

Пусть ^ - это одна из функций . Для этих трех функций выполнены следующие две эквивалентности ( законы ассоциативности и коммутативности ).

Ассоциативность:

(1)

Коммутативность:

(2)

Дистрибутивные законы:

(3)

Двойное отрицание:

(4)

Законы де Моргана (внесение отрицания внутрь скобок):

(5)

Законы упрощения:

(6)

Некоторые законы упрощения имеют собственные названия: эквивалентности в первой строке называются законами идемпотентности, - это закон противоречия, - это закон исключенного третьего. Эквивалентности в двух последних строках иногда называют законами 0 и 1.

Следующие две эквивалентности позволяют выразить импликацию и сложение по модулю 2 через дизъюнкцию, конъюнкцию и отрицание.

	(7)
			(8)

20. Двойственность - это термин математической логики, применяемый в случае таких пар понятий, как конъюнкция, дизъюнкция,  квантор общности и квантор существования. Двойственная функция - это функция,  полученная из исходной путём замены в ней  всех переменных на противоположные. Закон двойственности гласит, если формулы А и В равносильны, то и двойственные им формулы А*  и В* также равносильны. В теории исчисления высказываний этот закон назван принципом двойственности

        Американский логик А.Чёрч так определяет закон двойственности: "если  выводится А

и А* - дуал (двойственен) правильно построенной формулы, то выводится и не-А"

 Действительно, если  А Ú (В Ù С ) ≡ (А Ú В) Ù (А Ú С) , то принципу двойственности               А Ù (В Ú С ) ≡ (А Ù В) Ú (А Ù С)

        Принцип двойственности (дуальности) записывается в виде следующей формулы:

 если  А и если А* является дуалом (двойственным), правильно построенной формулы А , то А*, что читается так: "если А доказано, и если А* является дуалом А, то А* доказуемо". Символ называется знаком утверждения и словесно произносится "   доказуемо").

       Следует отметить, что принцип двойственности относится к булевым функциям, то есть к алгебре высказываний, в которой только знаки (операторы) конъюнкции, дизъюнкции и отрицания. Для операций импликации и эквивалентности выводятся специальные принципы, которые, как считает Чёрч,  являются следствием закона двойственности:

        1) если А ®  В и если А*  и  В* дуалы - правильно построенных формул А и В соответственно, то А*  ®  В*, где ® - знак импликации ( ...если, ...то)

          2) если А ≡  В и если А*  и  В* дуалы - правильно построенных формул А и В соответственно, то А*  ≡ В*, где ≡ - знак эквивалентности  ( ...если, и только если)

       Самодвойственной функцией называется такая функция, которая равносильна своей двойственной функции:

21. Метод применим к СДНФ и основывается на применении двух основных соотношений:

1. склеивание

2. поглощение

Суть метода заключается в последовательном выполнении всех возможных склеиваний и затем всех поглощений, что приводит к СкДНФ. Для получения МДНФ необходимо убрать из СкДНФ все лишние простые импликанты с помощью импликантной матрицы Квайна. В строках матрицы отмечаются простые импликанты, а в столбцах – конституэнты "1" булевой функции. Минимальные ДНФ строятся по импликантной матрице таким образом:

1) ищутся столбцы матрицы, имеющие только один крестик. Соответствующие этим крестикам простые импликанты называются базисными и составляют ядро булевой функции. Ядро обязательно входит в МДНФ.

2) рассматриваются различные варианты выбора совокупности простых импликант, которые накроют крестиками остальные столбцы матрицы, и выбираются варианты с минимальным суммарным числом букв в такой совокупности импликант.

 Пример: .

1) Избавимся от отрицаний и скобок:

2) Восстановим СДНФ, применяя развертывание:

3) Найдем СкДНФ, произведя все возможные склеивания:

4) Ищем МДНФ:

Ядро:

МДНФ:

22. В методе Квайна есть одно существенное неудобство. Оно связано с необходимостью полного попарного сравнения всех членов СДНФ ПФ на этапе нахождения всех простых импликант (при выполнении всевозможных операций неполного склеивания). При большом числе переменных применение метода Квайна становится затруднительным. Мак-Класки предложил модернизацию метода Квайна, дающую уменьшение числа сравнений. Идея метода Мак-Класки заключается в следующем: конституенты 1 в СДНФ представляются не в буквенном виде, а виде условных чисел – номеров соответствующих конституент. Вводится понятие индекса. Индексом целого числа называется количество 1 в двоичном представлении этого числа: 7 = 0111 – индекс равен 3, 0000 – индекс равен 0 и т.д. Если конституенты 1 склеиваются, то их индексы отличаются на 1, а в скобках должно быть число (их разности), равное целой степени 2 (по какой переменной склеиваются). Правило. Для того чтобы два числа m и n являлись номерами двух склеивающихся между собой конституент 1, необходимо и достаточно, чтобы их индексы отличались точно на 1, чтобы сами числа отличались друг от друга на степень 2, и чтобы число с большим индексом было больше числа с меньшим индексом. Так конституенты 1 с номерами 4 и 3, равными 0100 и 0011, не склеиваются, хотя их разности равны 1. Все конституенты 1 разбиваются на группы в соответствии с индексом и располагаются в порядке их возрастания. Группы отделяются друг от друга чертой. Склеиваться могут конституенты только соседних групп.

23. Исчисление высказываний (ИВ)

Каковы бы ни были формулы , следующие формулы называют аксиомами исчисления высказываний:

	(1)
			(2)

	(3)
		(4)

			(5)
	(6)

	(7)
			(8)

	(9)
				(10)

(11)

Как говорят, мы имеем здесь одиннадцать "схем аксиом"; из каждой схемы можно получить различные конкретные аксиомы, заменяя входящие в нее буквы на пропозициональные формулы.

Единственным правилом вывода исчисления высказываний является правило со средневековым названием "modus ponens" (MP). Это правило разрешает получить (вывести) из формул и формулу .

Выводом в исчислении высказываний называется конечная последовательность формул, каждая из которых есть аксиома или получается из предыдущих по правилу modus ponens.

24. В теории, построенной в согласии с аксиоматическим методом, начинают с небольшого количества неопределяемых (первичных) понятий, которые по предположению удовлетворяют определенным аксиомам. Прочие понятия, изучаемые в теории, определяются через первичные, и из аксиом и определений выводятся теоремы. Развитие математической теории в таком стиле – это первый шаг по направлению к её формализации.

В этой части мы исследуем применение аксиоматического метода в арифметике. Мы используем термин ``натуральные числа'' в смысле, отличающемся от обычного – ноль мы тоже включаем в натуральные числа. Такое использование этого термина обычно для зарубежных математиков. Мы пишем ``натуральные числа'' только чтобы не писать каждый раз ``целые неотрицательные числа''.

Аксиомы натуральных чисел

Мы рассматриваем множество w объектов называемых натуральными числами. Одно из натуральных чисел называется нулём и обозначается 0 . Для любого натурального числа n одно из натуральных чисел называется следующим за числом n и обозначается n' .

Множество натуральных чисел таково, что удовлетворяет следующим аксиомам:

Аксиома 1. Для любого натурального числа n: n'№ 0.

Аксиома 2. Для любых натуральных чисел m и n: если m'=n', то m = n.

Аксиома 3. Пусть A является подмножеством множества w со следующими свойствами:

0 О A;

для любого натурального числа n: если n О A, то n' О A.

Тогда A = w.

Эти аксиомы были введены Джузеппе Пеано в 1889 году.

25. –

26. Методику продемонстрируем на примере. Пусть требуется доказать:

.

Сначала поступают точно так же, как и по методике Вонга, только необходимо преобразовать клаузу таким образом, чтобы слева от символа Ю был ноль Ж:

Затем из дизъюнктов составляют резолюции до тех пор, пока не получится ноль.

Выпишем по порядку все посылки и далее начнем их «склеивать». Дизъюнкты можно перебирать автоматически в соответствии с возрастанием порядковых номеров. Такая стратегия поиска нуля очень непродуктивна. К решению данной задачи можно подойти творчески.

В итоге получим:

1. АЪ В	5. (1; 4)
2. СЪ А	6. (2; 4) С
3.	7. (3; 5)
4.	8. (6; 7) Ж

Иначе, произведенные раннее преобразования, можно представить в следующем виде:

27. Выберем множество истинностных значений . Также, выберем некоторое предметное множество . n-местным предикатом мы назовем функцию из 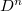в . Как и раньше, мы ограничимся классическим множеством -- истина и ложь, но оставляем потенциальную возможность его расширить. Предикаты могут быть 0-местными, в этом случае это хорошо нам известные пропозициональные переменные, принимающие какие-то истинностные значения, в происхождение которых мы не вникаем.

Рассмотрим следующий известный пример: каждый человек смертен, Сократ - человек, следовательно, Сократ - смертен. Мы можем формализовать это выражение с помощью предикатов: множество - это будет множество всех существ, - предикат "быть смертным", - предикат "быть человеком". Тогда фраза в полу-формальном виде выглядит так: Для каждого , такого, что верно , поэтому поскольку (Сократ), значит, что имеет место (Сократ). Чтобы построить новое исчисление, нам требуется указать 3 компонента: язык, аксиомы и правила вывода.

Основной задачей логики предикатов является установление истинности предикатных тождеств и клауз. Обозначим через Рi какой-либо предикат с произвольным числом аргументов, а через qi соответствующую ему кванторную группу. Тогда, например, закон дистрибутивности примет вид: q1P1 v (q2 Р2 & q3 Р3) = (q1 P1 v q2 P2) & (q1 P1 v q3 P3). В том, что он выполняется для одноместных предикатов, можно убедиться через процедуру конкретизации:

x = a, b ; q1 = x, Р1 = A(x); y = с, d ; q2 = y, P2 = B(y); z = e, f ; q3 = z P3 = C(z); [A(a) & А(b)] v ([В(с ) v B(d )] & [С(е) & С(f)]) = = ([А(a) & А(b)] v [В(с) v B(d)]) & ([А(a) & А(b)] v [С(e) & С(f)]) От того, что в квадратных скобках появится вместо дизъюнкции конъюнкция и наоборот, а также вместо одноместных предикатов будут фигурировать различные многоместные предикаты — суть тождества не изменится. Оно останется истинным в силу справедливости законов логики множеств и принципа суперпозиции, который гласит: замена какой-либо константы другой константой даже группой констант не может повлиять на истинность тождества. Именно отсюда проистекает наша уверенность в справедливости законов логики множеств и по отношению к предикатам. Те же самые рассуждения могут быть проведены и в отношении логики высказываний. Она отличается от логики Буля аксиомой порядка - q1P1, q2 Р2 => q1P1 Процедура конкретизации сводит предикатную аксиому порядка к npocтому высказыванию, так что если клауза верна для высказываний, она будет справедлива и для предикатов. Как показывает практика, много ошибок приходится на неправильное обозначение предикатов при их, в принципе, правильной идентификации. Следует помнить, что положительный предикат должен иметь больше единиц, чем отрицателъный. Будет допущена ошибка, если противоречие А1, -А2 => 0 записать как А2, -А1 => 0 .