7.2. Методи статистичного аналізу

Перший метод статистичного аналізу — це дисперсійний аналіз, або метод статистичної обробки спостережень. Застосовується для оцінювання впливу на величину, що спостерігається за різних чинникових ознак, від яких ця величина залежить.

Кожне вимірювання залежить від певної кількості параметрів, які можуть набувати або дискретні, або неперервні значення. Залежність розглядають у вигляді лінійної комбінації параметрів з коефіцієнтами:

y_i= b₁x_1j + b₂x_2j +…+ b_mx_mj + e_i

де x_ij — параметри; b_i — коефіцієнти; е_і — випадкова похибка вимі­рювання, і =

Коефіцієнти b називають чинниками. Рівняння називають лінійною багаточинниковою моделлю.

У дисперсійному аналізі параметри x_ij зазвичай беруть рівними нулю або одиниці, що вказує на те, які з чинників враховують за та­кого аналізу.

Однією з проблем в економічному моделюванні є проблема ви­вчення взаємозв'язку економічних показників. Другий метод статис­тичного аналізу — це регресійний аналіз.

Розглянемо залежність двох змінних: х та у. Припустімо, що є ряди значень змінних і відповідні їм точки нанесені на графік.

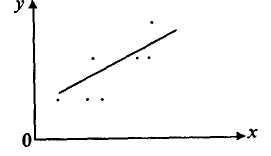
Рис. 7.1. Лінійна залежність двох змінних

Для дослідних даних за емпіричну формулу можна прийняти лінійну залежність у = ах + b. Наприклад, у кейнсіанській функції споживання існує лінійна пряма залежність споживання від доходу, функція інвестицій також лінійно відображає обернену залежність відсоткової ставки від обсягу інвестицій.

Отже, ми повинні оцінити рівняння регресії у = f(х) — формулу ста­тистичного зв'язку між змінними. Якщо ця формула лінійна, йдеться про лінійну регресію. Формула статистичного зв'язку двох змінних називається парною регресією, а від кількох змінних — множинною регресією.

Для оцінювання невідомих параметрів за результатами вимірювань використовують метод найменших квадратів. За його допомогою спо­чатку визначають функціональну залежність представлення даних дос­лідження, а потім для цієї залежності добирають параметри. Для дослі­дних даних (рис. 7.2) за емпіричну формулу краще прийняти квадра­тичну у = ах² + bх + с. Для дослідних даних (рис. 7.3.) за емпіричну формулу краще прийняти гіперболічну: у = а + b/х. Наприклад, крива Філіпса для короткострокового періоду відображає гіперболічну за­лежність між темпами інфляції та рівнем безробіття.

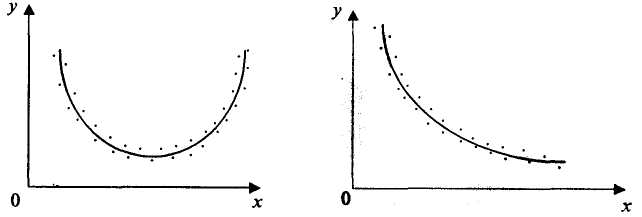
Рис. 7.2. Квадратична залежність Рис. 7.3. Гіперболічна залежність

За методом найменших квадратів потрібно мінімізувати суму:

S = Σ(y_i – y(x_i))²→min

де x_i, у_i і—значення дослідних даних; у(х_i) — значення функції, обчис­лене за емпіричною залежністю у точці x_i; і= 1,п.

Якщо залежність визначена як лінійна, сума набуває вигляду:

F =

Для квадратичної залежності:

F =

Мінімум функції досягається у точці, в якій похідна суми за пара­метрами дорівнює нулю. Для лінійної залежності система рівнянь, утворена з похідних, набуває вигляду

Для визначення параметрів розв'язуємо систему двох рівнянь з двома невідомими а та b.

Приклад. Дослідні дані про значення X та У наведені у таблиці.

X	1	2	3	4	5	6
У	10	12	4	5	-1	-2

Аналіз дослідних даних засвідчив, що за емпіричну залежність можна використати лінійну: у = ах + b. Визначимо за методом най­менших квадратів значення а та b.

Проміжні результати запишемо в таблицю.

і	xi	yi		xiyi
1	1	10	1	10
2	2	12	4	24
3	3	4	9	12
4	4	5	16	20
5	5	-1	25	-5
6	6	-2	36	-12
2	21	28	91	49

За обчисленими даними система лінійних рівнянь набуває вигляду:

Розв'язавши її, одержимо а = -2,8; b = 14,46.

Емпірична формула має вигляд: у = -2,8х + 14,46.