21. Методы решения тригонометрических уравнений.

Методы решения тригонометрических уравнений.

1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции с последующей заменой переменной.

2. Решение уравнений методом разложения на множители.

3. Решение однородных уравнений.

4. Введение вспомогательного аргумента.

Рассмотрим каждый из перечисленных методов на примерах, но более подробно остановимся на двух последних, так как два первых мы уже использовали при решении уравнений.

1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции.

2. Решение уравнений методом разложения на множители.

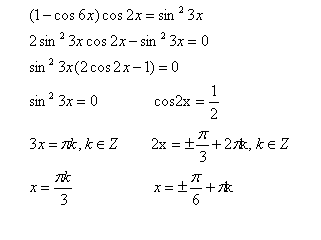
3. Решение однородных уравнений.Однородными уравнениями первой и второй степени называются уравнения вида:

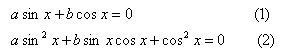
соответственно (а ≠ 0, b ≠ 0, с ≠ 0 ).

При решении однородных уравнений почленно делят обе части уравнения на cosx для (1) уравнения и на cos 2 x для (2). Такое деление возможно, так как sinx и cosx не равны нулю одновременно – они обращаются в нуль в разных точках. Рассмотрим примеры решения однородных уравнений первой и второй степени.

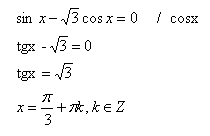Запомним это уравнение: при рассмотрении следующего метода – введение вспомогательного аргумента, решим его другим способом.

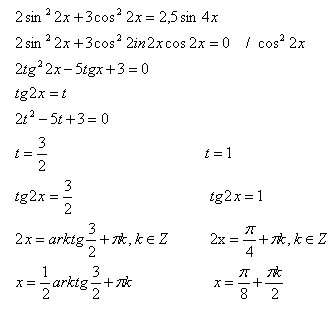
4. Введение вспомогательного аргумента.

Рассмотрим уже решенное предыдущим методом уравнение:

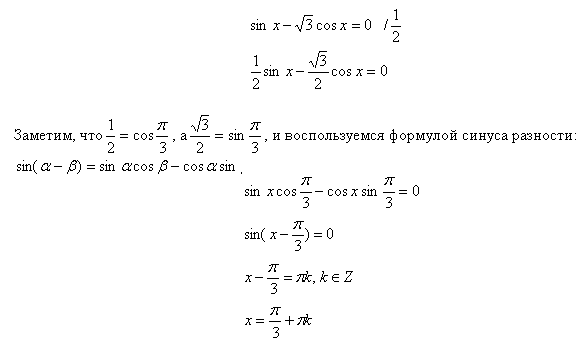
Как видим, получается тот же результат.

Рассмотрим еще один пример:

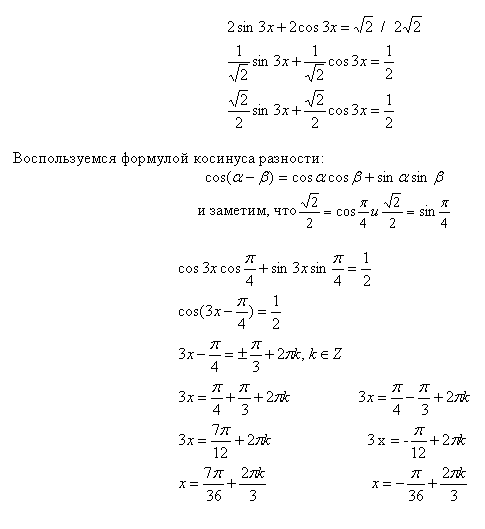
В рассмотренных примерах было, в общем, понятно, на что требуется разделить исходное уравнение, чтобы ввести вспомогательный аргумент. Но может случиться, что не очевидно, какой делитель выбрать. Для этого существует специальная методика, которую мы сейчас и рассмотрим в общем виде. Пусть дано уравнение:

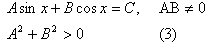
Разделим уравнение на квадратный корень из выражения (3), получим:

asinx + bcosx = c ,

тогда a 2 + b 2 = 1 и, следовательно, a = sinx и b = cosx . Используя формулу косинуса разности, получим простейшее тригонометрическое уравнение:

которое легко решается.

Решим еще одно уравнение:

Сведем уравнение к одному аргументу – 2 x с помощью формул двойного угла и понижения степени:

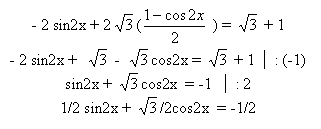
Аналогично предыдущим уравнениям, используя формулу синуса суммы, получаем:

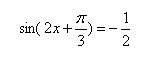
что тоже легко решается.

22. Простейшие тригонометрические неравенства.

Основной способ решения тригонометрических неравенств состоит в их сведении к неравенствам вида

sinx Ъ a,     cosx Ъ a,     tgx Ъ a,     ctgx Ъ a,

(1)

где a О R, символ "Ъ" означает знак сравнения и заменяет любой из знаков ">",   " ≥ ",   "<",  " ≤" и использовании следующих утверждений.

Утверждение 1. Множество решений неравенства

sinx > a

(2)

есть

R, если a < -1;

(arcsina + 2pk; p - arcsina + 2pk), если -1 ≤ a < 1;

Пустое множество, если a ≥ 1.

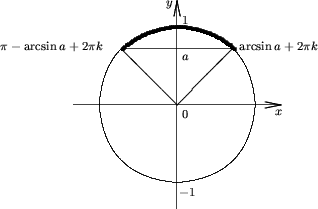
Утверждение 2. Множество решений неравенства

sinx < a

(3)

есть

R, если a > 1;

(-p - arcsina + 2pk; arcsina + 2pk), если -1 < a ≤ 1;

Пустое множество, если a ≤ -1.

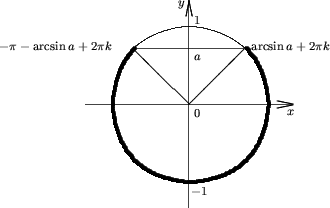
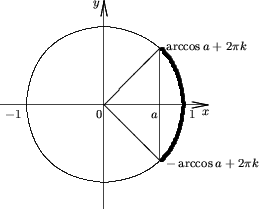
Утверждение 3. Множество решений неравенства

cosx > a

(4)

есть

R, если a < -1;

(2pk - arccosa; 2pk + arccosa), если -1 ≤ a < 1;

Пустое множество, если a ≥ 1.

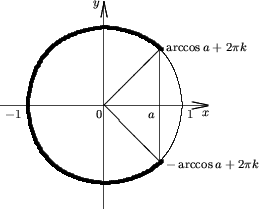
Утверждение 4. Множество решений неравенства

cosx < av

(5)

есть

R, если a > 1;

(2pk + arccosa; 2p(k + 1) - arccosa), если -1 < a ≤ 1;

Пустое множество, если a ≤ -1.

Утверждение 5. Множество решений неравенства

tgx > a

(6)

есть 

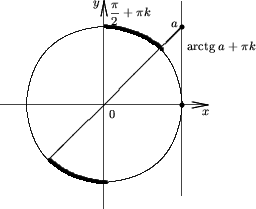
Утверждение 6. Множество решений неравенства

tgx < a

(7)

есть 

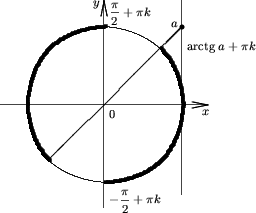
Утверждение 7. Множество решений неравенства

ctgx > a

(8)

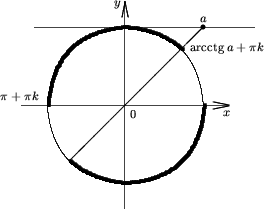
есть  (pk; arcctga + pk).

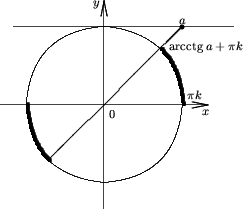
Утверждение 8. Множество решений неравенства

ctgx < a

(9)

есть  (arcctga + pk; p(k + 1))