- •2. Показательные уравнения
- •3. Решение показательных неравенств
- •4. Логарифмическая функция её свойства и график
- •6, 7,8 Логарифм с произвольным основанием.
- •Логарифмические уравнения.
- •10,11 Простейшие логарифмические неравенства.
- •12. Определение тригонометрических функций
- •13. Основные тригонометрические тождества
- •14. Формулы приведения тригонометрических функций.
- •15. Знаки тригонометрических функций. Формулы сложения.
- •Формулы сложения
- •16. Тригонометрические функции двойного и половинного аргумента. Формулы понижения степени. Формулы двойного угла
- •17. Преобразование суммы и разности тригонометрических функций в произведение.
- •Тригонометрические функции, их свойства и графики.
- •Обратные тригонометрические функции.
- •Простейшие тригонометрические уравнения.
- •21. Методы решения тригонометрических уравнений.
- •Простейшие тригонометрические неравенства.
- •Предел функции в точке. Теоремы о пределах.
- •24.Предел функции на бесконечности.
- •25. Раскрытие неопределенностей при вычислении пределов функций.
- •26. Первый и второй замечательные пределы.
- •27. Непрерывность и точки разрыва функции
- •28. Определение производной.
- •29. Производная суммы, произведений, частного функций
- •30. Производная сложной функции.
- •31. Производная показательной и логарифмической функции
- •32. Производные тригонометрических функций.
- •33. Производные обратных тригонометрических функций
15. Знаки тригонометрических функций. Формулы сложения.
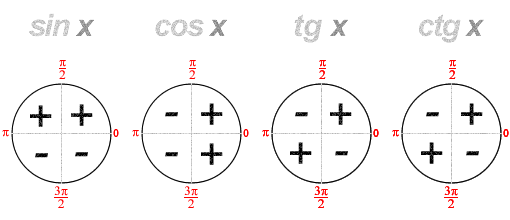
Формулы сложения
sin (α + β) = sin α · cos β + sin β · cos α
sin (α - β) = sin α · cos β - sin β · cos α
cos (α + β) = cos α · cos β - sin α · sin β
cos (α - β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)
16. Тригонометрические функции двойного и половинного аргумента. Формулы понижения степени. Формулы двойного угла
cos 2α = cos² α - sin² α
sin 2α = 2sin α · cos α
tg 2α = (2tg α) ÷ (1 - tg² α)
ctg 2α = (ctg² α - 1) ÷ (2ctg α)
Формулы половинного угла.
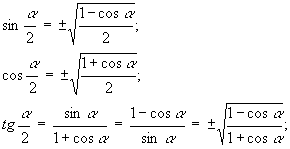
Формулы понижения степени
sin² α = (1 - cos 2α) ÷ 2
sin³ α = (3sin α - sin 3α) ÷ 4
cos² α = (1 + cos 2α) ÷ 2
cos³ α = (3cos α + cos 3α) ÷ 4
sin² α · cos² α = (1 - cos 4α) ÷ 8
sin³ α · cos³ α = (3sin 2α - sin 6α) ÷ 32
17. Преобразование суммы и разности тригонометрических функций в произведение.

Тригонометрические функции, их свойства и графики.
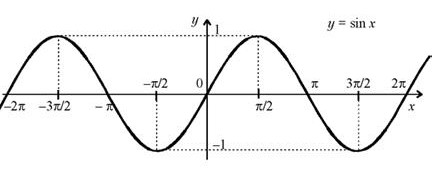
СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК
а) Область определения: D (sin x) = R .
б) Множество значений: E (sin x) = [ – 1 , 1 ] . в) Четность, нечетность: функция нечетная.
г)
Периодичность:
функция периодическая с основным
периодомT =2![]() д) Нули
функции:
sin x =
0 при x =
n, n
д) Нули
функции:
sin x =
0 при x =
n, n ![]() Z.
Z.
е) Промежутки знакопостоянства:
![]() ;
; ![]() .
.
ж) Промежутки
монотонности:
![]()
![]() .
.
з) Экстремумы:
![]() ;
; ![]() .
.
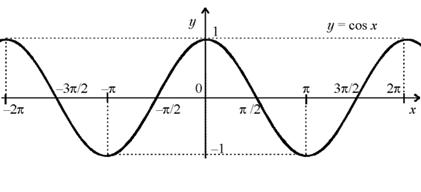
СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК
а) Область определения: D (cos x) = R .
б) Множество значений: E (cos x ) = [ – 1 , 1 ] . в) Четность, нечетность: функция четная.
г)
Периодичность: функция
периодическая с основным периодом T
=2
д) Нули
функции:
cos x =
0 при x = ![]() +
n, n
Z.
+
n, n
Z.
е) Промежутки знакопостоянства:
![]() ;
;
![]() .
.
ж) Промежутки монотонности:
![]() ;
;
![]() .
.
з) Экстремумы:
![]() ;
; ![]() .
.
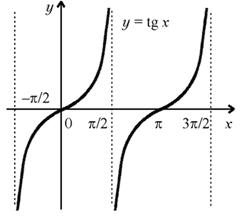
СВОЙСТВА ФУНКЦИИ y = tg x И ЕЕ ГРАФИК
а) Область определения: D (tg x) = R \ { /2 + n( n Z ) }.
б) Множество значений: E (tg x ) = R . в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T =
д) Нули функции: tg x = 0 при x = n, n Z.
е) Промежутки знакопостоянства:
![]() ;
;
![]() .
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
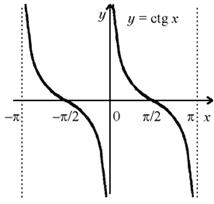
СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК
а) Область определения: D (ctg x) = R \ { n( n Z ) }.
б) Множество значений: E (ctg x ) = R . в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = д) Нули функции: ctg x = 0 при x = /2 + n, n Z.
е) Промежутки
знакопостоянства ;
![]() ;
; ![]() .
.
ж) Промежутки монотонности: функция убывает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.