2. Построение проекций точек

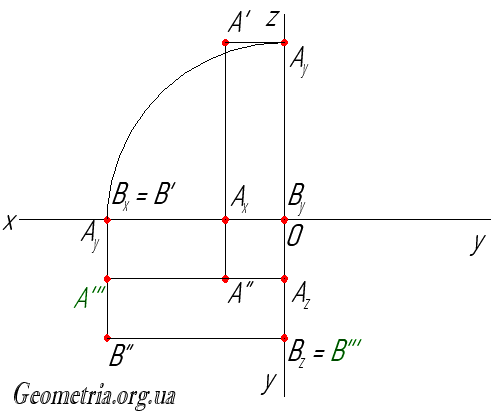
Точки А и В в плоскости π3 имеют следующие координаты: А’’’(y,z); B’’’(y,z).

При этом точки А” и А’’’ лежат одном перпендикуляре к оси z, так как координата z у них общая; точно также на общем перпендикуляре к оси z лежат точки В” и B’’’. Для определения профильной проекции точки А отложим по оси у значение соответствующей координаты, найденное ранее (на рисунке это сделано с помощью дуги окружности радиуса А_уО) , после чего проведем перпендикуляр из точки А_у до пересечения с перпендикуляром, восстановленным из точки А” к оси z. Точка пересечения этих двух перпендикуляров определяет положение точки А’’’.

Точка B’’’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции точки B в данной задаче необходимо лишь провести перпендикуляр из точки В” к оси z, и точка пересечении этого перпендикуляра с осью z и есть точка B’’’.

3. Определение положения точек в пространстве

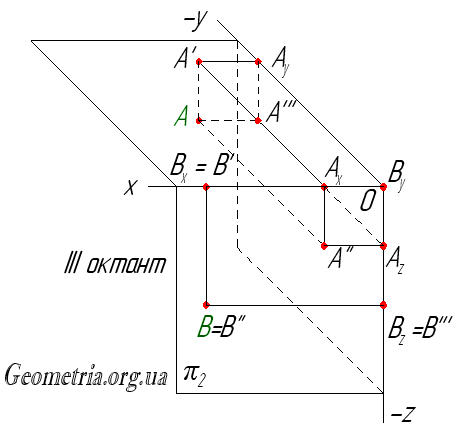
Наглядно представляя себе пространственный макет, составленный из плоскостей проекций π1, π2 и π3, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что точка А расположена в III октанте, а точка В лежит в плоскости π2.

Другим вариантом решения данной задачи можно считать метод исключения. Например, координаты точки А(10,-30,-10). Положительная абсцисса x позволяет судить о том, что точка расположена в первых четырех октантах. Отрицательная ордината y говорит о том, что точка находится во втором или третьем октантах, и, наконец, отрицательная аппликата z указывает на то, что А расположена в третьем октанте.

Координаты точки В(30,0,-20). Ордината точки В равна нулю, что позволяет сделать вывод о том, что эта точка расположена в плоскости проекций π2. Положительная абсцисса и отрицательная аппликата точки B указывают на то, что она расположена на границе третьего и четвертого октантов.

4. Построение наглядного изображения точек в системе плоскостей π1, π2, π3.

После того, как мы определили, что точка А находится в третьем октанте, а точка В лежит в плоскости π2, построим пространственный макет III октанта, представляющий собой прямоугольный трехгранник, у которого гранями являются плоскости проекций π1, π2, π3.

Построение наглядного изображения точки А(10,-30,-10) начнем с построения её горизонтальной проекции А’. Отложив по оси абсцисс и ординат соответствующие координаты, найдем точки А_х и А_у. Пересечение перпендикуляров, восстановленных из точек А_х и А_у соответственно к осям x и y определяет положение точки A’. Отложив от точки A’ параллельно оси z отрезок А’А, длина которого равна величине аппликаты точки А, в сторону отрицательных значений оси z, находим положение точки А.

Наглядное изображение точки В(30,0,-20) строится аналогично – в плоскости π2 по осям x и z нужно отложить соответствующие координаты, и пересечение перпендикуляров, восстановленных из точек B_х и B_z к осям x и z, определит положение точки B.

6) Пространство Евклида, дополненное несобственными элементами, называется проективным. Сущность введения несобственных элементов заключается в следующем: 1) каждая прямая, кроме множества обыкновенных точек, имеет одну несобственную; несобственная точка прямой есть эквивалент понятия "направление прямой"; 2) параллельные прямые имеют общую несобственную точку (пересекаются в ней); 3) плоскость имеет множество несобственных точек, которые образуют несобственную прямую плоскости; 4) параллельные плоскости имеют общую несобственную прямую (пересекаются по несобственной прямой); 5) множество всех несобственных точек и прямых пространства образует несобственную плоскость. Дополнение евклидова пространства несобственными элементами позволяет ликвидировать исключения в основных положениях элементарной геометрии и утверждать: 1) каждые две прямые, принадлежащие одной плоскости, всегда пересекаются (в собственной или несобственной точках); 2) две любые плоскости пространства всегда пересекаются (линия пересечения - собственная или несобственная прямая); 3) прямая и плоскость всегда пересекаются (в собственной или несобственной точках). следовательно, проекцией точки C, принадлежащей плоскости П1' II П1 будет несобственная точка C1.

7) Алгоритм решения задачи на построение линии пересечения двух поверхностей: 1. Вводим дополнительную плоскость (поверхность), чаще всего плоскость частного положения так, чтобы она пересекала обе заданные поверхности;

2. Строим линию пересечения посредника с первой поверхностью, со второй поверхностью;

3. Смотрим, где построенные линии пересекаются. Там будут искомые точки.

4. Алгоритм повторяем столько раз сколько необходимо для выяснения характера линии пересечения. Полученные точки соединяем и получаем искомую линию пересечения двух поверхностей. Посредник нужно выбирать так, чтобы проекции линий его пересечения с заданными поверхностями, были простейшими, т.е. чтобы их можно было построить с помощью циркуля и линейки.

9) Начертательная геометрия - видео решение задач

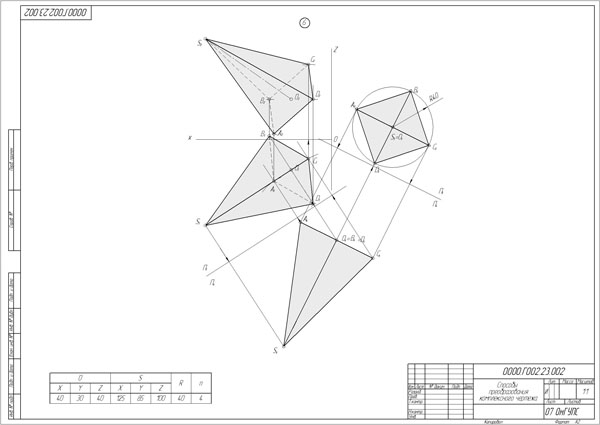
З а д а ч а 6. По заданным координатам высоты OS и радиусу R описанной окружности основания построить проекции правильной n-гранной пирамиды методом перемены проекций.

Теория. При решении задач часто возникает необходимость такого преобразования комплексного чертежа, при котором прямые и плоскости общего положения стали бы прямыми и плоскостями частного положения. Одним из способов такого преобразования является метод перемены (замены) плоскостей проекций.

Сущность метода перемены плоскостей проекций состоит в следующем: положение геометрических элементов в пространстве не изменяется, плоскость же проекций П1 или П2 заменяют новой плоскостью. Такую замену проводят последовательно: сначала заменяют одну плоскость, затем другую, если есть необходимость в двойной замене.

При построении проекции фигуры на новой плоскости проекций происходит переход от одного эпюра к другому, на котором соответственные проекции точек также расположены на линиях связи. Координата точки на новой плоскости проекций равна координате точки на заменяемой плоскости проекций.

Решение задачи начинаем с построения проекции высоты пирамиды по заданным для варианта 24 координатам. Цель замены плоскостей проекций в данной задаче  привести высоту пирамиды общего положения в положение проецирующей прямой. При этом высота пирамиды спроецируется в точку и основание ее может быть легко построено, так как для правильной пирамиды оно спроецируется в натуральную величину.

Указанное преобразование достигается двумя заменами плоскостей проекций.

1) Заменяем плоскость П₂ на П₄, чтобы высота пирамиды стала линией уровня (фронталью). Новую ось проекций в системе П₁/П₄ проводим параллельно O₁S₁, проекции точек О₄ и S₄ строим по линиям связи к новой оси с сохранением координаты z.

2) Заменяем плоскость П₁ на П₅, чтобы высота пирамиды стала перпендикулярна плоскости проекций. Новая ось в системе П₅/П₄ проводится перпендикулярно к проекции O₄S₄, при этой замене сохраняется координата y.

На плоскости П₅ строим основание пирамиды описанной окружности основания с заданным радиусом 40 мм и четырьмя гранями. По построенной проекции пирамиды на плоскости П₅ обратным ходом строим ее проекцию на плоскости П₄, затем на П₁ и П₂. На всех проекциях определяем видимость граней и ребер пирамиды по конкурирующим точкам.

10)

Пересечение прямой общего положения с плоскостью общего положения

В предыдущих пунктах мы рассмотрели случаи пересечения прямой и плоскости при частном расположении пересекающихся фигур. Теперь обратимся к решению одной из главных позиционных задач: нахождение точки пересечения прямой общего положения с плоскостью общего положения. Построим точку К - точку пересечения прямой общего положения а с плоскостью общего положения , заданную тремя точками А, В, С. Нажмите на картинку для просмотра... Алгоритм построения точки пересечения: Например на П1 проведем через заданную прямую а1 вспомогательную горизонтально проецирующую плоскость : а  и  П1. Построим m1 - линию пересечения вспомогательной плоскости  с заданной плоскостью . Отметим точки 11 и 21 - точки пересечения прямой m1 и отрезков А1В1 и В1С1 соответственно. Построим фронтальную проекцию прямой m, учитывая принадлежность точек 1 и 2 сторонам треугольника АВС. Находим точку К2 - точку пересечения прямых m2 и а2: К2=m2 а2. По линии связи находим первую проекцию точки К - точку К1. Определяем видимость прямой а с помощью метода конкурирующих точек. На П2, правая часть прямой а2 (относительно точки К2) - видима, а левая часть прямой а2 - невидима. На П1, левая часть прямой а1 (относительно точки К1) - невидима, а правая часть прямой а1 - видима.