
- •Понятие модели. Понятие моделирования. Типы моделирования.
- •3.Аналоговое моделирование. Терминология. Последовательность действий при моделировании. Положения, используемые при переходе от одной системы к другой.
- •4.Понятие системы. Свойства системы. Типы систем. Хар-ки систем.
- •5.Понятие управления(у). Общее уравнение у. Критерий качества. Оптимальное у. Причины приближенного решения задач моделирования управления. Основные положения при разработке систем управления.
- •6.Решение систем линейных уравнений. Метод Гаусса. Контроль точности при решении. Метод простой итерации, условие сходимости.
- •7.Решение нелинейных уравнений. Отделение корней. Метод половинного деления. Метод хорд. Метод касательных.
- •10.Понятие численного интегрирования. Нахождение интеграла методом прямоугольников, методом трапеций, методом Симпсона.
- •14.Понятие оптимизации. Типы задач оптимизации.
- •15.Линейное программирование (лп). Геометрическая интерпретация задачи лп.
- •18.Цели и задачи исследования мат моделей систем. Этапы построения моделей.
14.Понятие оптимизации. Типы задач оптимизации.
Оптимизация-выбор наилучшего варианта решения среди множества допустимых, с помощью некоторого критерия. При этом критерий формулируется в виде некоторой ф-ции, к-я наз-ся целевой или ф-ей кач-ва
Типы задач оптимизации:
Если ф-я цели линейная (
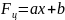 ),то
задача линейного программирования
),то
задача линейного программированияЕсли
 ,
то это квадратичное программирование
,
то это квадратичное программированиеЕсли функция цели нелинейная, то задача наз-ся задачей нелинейного программирования
В зависимости от размерности Х различают одномерные, двухмерные и многомерные задачи.
В зависимости от количества экстремумов функции цели различают одноэкстремальные и многоэкстремальные задачи.
Задачи различаются в зависимости от вида ограничений: безусловная и условная оптимизация.
В зависимости от значений, к-е принимает делится на задачи вещественного и дискретного программирования.
По области применения: в экономике, в задачах управления – линейные многомерные задачи с ограничениями.
В задачах математического программирования заставить обратиться в ноль все частные производные Fy одновременно невозможно, поскольку min или max этой функции достигается не во внутренних точках заданной области, а на ее границах. Отсюда возникает самостоятельная сложная задача.
15.Линейное программирование (лп). Геометрическая интерпретация задачи лп.
Общий вид:
Задана ф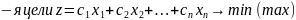
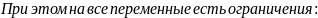

@ - любые знаки
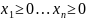
Канонический вид:

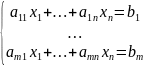
т.о. ЛП – мат. Дисциплина, к-я изучает методы нахождения наибольшего или наименьшего знач-я ф-ции нескольких переменных, при условии, что эти переменные удовлетворяют конечному числу линейных ур-ий и неравенств.
Ограничения
в виде неравенств легко переводятся в
ограничения в виде равенств. Вводится
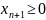 дополнительных
переменных и задача сводится к канонической
форе, но с большим числом неизвестных.
Для того, чтобы наложить условие
неотрицательности на все переменные
при канонической форме:
дополнительных
переменных и задача сводится к канонической
форе, но с большим числом неизвестных.
Для того, чтобы наложить условие
неотрицательности на все переменные
при канонической форме:
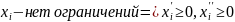
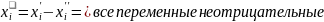
Любое неотриц. решения системы наз-ся допустимы решение, из этих допустимых решений выбираем min(max) и оно наз-ся оптимальным решением. Оптимальное решение не обязательно единственное.
Суть ЛП: из множ-ва допустимых решений выбрать то, к-е обращает линейную форму минимум.
Задачу нахождения оптимальной ф-ции ЛП можно интерпретировать геометрически. Для этого все ограничения представляют в виде неравенств, тогда каждое нер-во в n-мерном пространстве определяет полупространство расположенное по одну сторону от плоскости, к-е записывается:
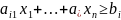 -
полупространство
-
полупространство
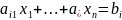 -
плоскость
-
плоскость
Геометрический смысл ЛП – отыскание в многоугольнике Ω точки, к-я наиболее (наименее) уклонена от z=0.
16.Нелинейное программирование (НП). Аналитические условия решения задач НП. Типы методов НП. Методы решения задач одномерной минимизации. Метод дихотомии. Метод золотого сечения. Методы решения задач многомерной оптимизации. Метод случайного поиска. Метод деформируемого многогранника Нелдера-Мида.
Нелинейное программирование — раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и (или) областью допустимых решений, определенной нелинейными ограничениями.
В краткой форме задачу н. п. можно записать так:
F (x) → max при условиях g (x) ≤ b, x ≥ 0, где x — вектор искомых переменных; F (x) — целевая функция; g (x) — функция ограничений (непрерывно дифференцируемая); b — вектор констант ограничений (выбор знака ≤ в первом условии здесь произволен, его всегда можно изменить на обратный).
Решение задачи НП (глобальный макс или мин) может принадл либо границе, либо внутренней части допустимого множества. Задача состоит в выборе таких неотрицательных значений переменных, подчиненных системе ограничений в форме неравенств, при к-х достигается макс (или мин) данной ф-и. При этом не оговариваются формы ни целевой функции, ни неравенств. Могут быть разные случаи: целевая функция нелинейна, а ограничения линейны; целевая функция линейна, а ограничения (хотя бы одно из них) нелинейны; и целевая функция, и ограничения нелинейны.
Задачи, в к-х число переменных и (или) число ограничений бесконечно, называются задачами бесконечномерного н. п. Задачи, в которых целевая ф-я и (или) ф-и ограничений содержат случайные элементы, называются задачами стохастического н. п.
Обобщенная постановка задачи нелинейного программирования
Если
 нелин
ф-я, то из мат-ки известны необход и
достат усл сущ ее экстремума. В одномерном
случае имеем:
нелин
ф-я, то из мат-ки известны необход и
достат усл сущ ее экстремума. В одномерном
случае имеем:

-если x* - arg max f(x): необ f’(x*)=0, дост условия f”(x*)<0
-если x* - arg min f(x): необ f’(x*)=0, дост условия f”(x*)>0
В многомерном случае имеем: Max grad =0

Метод дихотомии.
На каждом шаге итерационного процесса использ следующие соотношения:
x1(n)
= (an+bn)/2-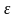 /2
x2(n)
= (an+bn)/2+
/2
/2
x2(n)
= (an+bn)/2+
/2
Возможны след варианты:
- f(x1(n))>f( x2(n)) -> an+1= x1(n) ; bn+1=bn
- f(x1(n))< f(x2(n)) -> an+1= an ; bn+1=x2(n)
- f(x1(n))= f(x2(n)) -> an+1= x1(n) ; bn+1= x2(n)

Метод золотого сечения.
Более эффективный метод, и самый распространенный.Считается, что отрезок поделен по методу золотого сечения, если: l2 / l = l1 / l2; если l=1, то l1= 0.382, l2=0.618. Общая процедура метода сводится к след формулам:
x1(n) =an+0.382(bn-an)
x2(n) =bn-0.382(bn-an)
Возможны след варианты:
- f(x1(n))>f( x2(n)) -> an+1= x1(n) ; bn+1=bn
- f(x1(n))< f(x2(n)) -> an+1= an ; bn+1=x2(n)
- f(x1(n))= f(x2(n)) -> an+1= x1(n) ; bn+1= x2(n)
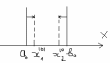
Общая характеристика метода многомерного поиска
f(X) X=(x1,x2,xn) Суть: последовательно фисксируются значения всех переменных xi кроме xj j=1..n переходим от многомерной ф-ии к одномерной. Этот метод находит xj*, фиксирует это значение и переходит к новой координате, цикл заканчивается после перебора всех переменных. Метод может быть использован только, когда переменные xi мало зависят друг от друга.
Метод Нелдера-Мида или метод деформируемого многогранника
В пространстве поиска строится (произвольно) исходный симплекс – правильный многогранник: тетраэдр и др. Вычисляются значения целевой ф-ции в вершинах. Определяется в вершинах, в которых значения ф-ци больше. Эта вершина отбрасывается и строится новый симплекс проецирования отброшенной вершины через центр тяжести исходного симплекса. Таким образом определяется направление поиска, в котором делаются пробные шаги. Если эти шаги удачны, то выполняется растяжение. Если неудачны, то выполняется сжатие. Критерием окончания поиска может служить, например, площадь, объем полученного многогранника или абсолютное изменение переменных |xi-xik+1|≤ε i=1,n.
Таким образом, метод позволяет выделить окрестность существования экстремума и поэтому применяется, как правило, на предварительном исследовательском этапе оптимизации.
