5.Понятие управления(у). Общее уравнение у. Критерий качества. Оптимальное у. Причины приближенного решения задач моделирования управления. Основные положения при разработке систем управления.

Суть управления в том, что оно является вмешательством в естественный ход пр-са м в его изменение. Управление – это организация того или иного пр-са, к-я обеспечивает достижение поставленных целей.

Некоторые величины, используемые в управлении в силу физических особенностей не могут или не должны превосходить конкретных пределов. Математически они выражаются в виде систем уравнений или неравенств. Математическое выражение, дающее оценку степени выполнения наложенных требований называют критерием качества управления.

Способ управления удовлетворяющий требованиям и ограничениям и обращающий в min критерий качества управления называется оптимальным управлением.

В реальных задачах задачи управления решаются приближенно т.к.:

1. Точные ур-я связи обычно не известны и заменяются ур-ми мат.модели изучаемой системы q^*=q^*( )

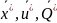2. Неточность данных о состоянии объекта Х и воздействия определенной среды Q. Она может возникнуть по след. 2м причинам:

А)в мат.модели входят только те величины, к-е можно наблюдать и измерять в пр-се управления

Б)в наблюдаемом 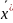уже сод-ся измерения и ошибки, возникшие в пр-се передачи и преобр-я инф.

3. Приближенные ограничения

4. Ошибки управления, к-е связаны с конкретной реализацией упр.воздействия. Как показатель эффективности можно использовать: Q= -разность между расчетными и действит.значениями целей.

Задача управления: выбрав идеальный вектор состояния , необходимо найти и реализовать вектор упр.воздействий 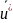, к-й обеспечивает наивысшее качество управления в смысле экстремума функционала Q при наличии заданных ограничений.

Основные положения, к-е необх.исп-ть при разработке систем управления:

1. Для каждой СУ дБ четко сформулированы цели (1 или несколько), и определено конечное состояние объекта упр.

2. У каждой СУ дБ свобода выбора траектории движения к конечной цели.

3. Чтобы выбрать наилучшую из возможных траекторий движения, система должна иметь способ их сравнения.

4. СУ должна располагать опред.ресрсами, к-е обеспечивают реализацию упр.воздействий и ведут движение системы по заданной траектории.

5. Чтобы принять решение о необх.упр.воздействий, нужно иметь действит.сведения о состоянии системы.

6. Чтобы из набора возможных упр.возд. выбрать наиболее целесообразные, необх.иметь сведения о поведении системы под действием этих воздействий. Для этого необх.мат.модель изучаемой системы.

Все параметры, вх.в ур-е связи, в реальных задачах зависят от времени, поэтому логично добавить время в ур-е связи. q=q( ,t), t можно рассматривать как непрерывное, так и дискретное на интервале времени.

В общем случае сов-ть зависимостей вых.хар-к системы от t наз-ся вых.траекторией, а q(t)-закон функционирования системы. Этот закон мб задан в виде функции, функционала, логических или табл.условий, алгоритмических и тд.