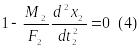1. Понятие модели. Понятие моделирования. Типы моделирования.

Требования, предъявляемые к моделям. Математическое моделирование. Классификация математических моделей.

Модель – это материальный или же мысленно представляемый объект, который в процессе познания замещает объект – оригинал, при этом сохраняет некоторые важные для данного исследования типичные его черты. Модель всегда создается для конкретного исследования.

Моделирование – это представление различных характеристик физ. или абстрактного объекта – оригинала с помощью другого объекта – модели, а так же выявление свойств объектов-оригиналов путем построения и исследования модели.

Типы моделирования:

1. Материальное – воспроизводит динамические, геометрические и функциональные характеристики объекта:

А) натуральное – производится над реальным объектом с последующей обработкой результатов экспериментов (научный эксперимент, комплексные испытания, производственный эксперимент)

Б) физическое – оригинал и модель имеют одинаковую физ.природу, модель – уменьшенная или увеличенная копия оригинала, может протекать в реальном времени, в модельном времени и без учета времени.

В) аналоговое – основано на аналогии, объект и модель имеют разную физ.природу, но подчиняются одинаковым законам и мат.ур-ям и описываются ими.

2. Идеальное – основано на мысленных сходствах модели и оригинала, носит теоретический х-р.

А) интуитивная модель – не подлежит формализации, используется в тех областях, где процесс познания нах-ся на довольно низкой стадии.

Б) знаковое – подлежит формализации, использует формулы, чертежи, схемы, графики и тд. К нему относится мат.мод-е (устанавливается соответствие данному реальному объекту некоторого мат.объекта, который мб описан на языке мат.логики, различных мат.методов и носит теор.х-р)

Мат.модель – совокупность мат.объектов (числа, вектора, множества, формулы) или отношения между ними, к-е адекватно отображает свойства исследуемого объекта.

Классификация:

1. По области применения – технические, экономические, биологические и др.

2. В зависимости от класса решаемых задач – дескрипторные, оптимизационные, имитационные, информационные и тд.

3. По хар-ру отображаемых св-в:

3.1 Структурные:

А) топологические – отображаю только состав и взаимодействие между эл-ми, описываются таблицами, списками, графиками Б) геометрические – это топологическая модель, к к-й добавлена форма элемента, для их описания необходимо давать ур-е поверхности

3.2 Функциональные – отображают физ.и инф.процессы, для их описания исп-ся ур-я, системы ур-ний, к-е связывают между собой параметры объекта:

Y=F(X,Q),где Y – выходные парам., X – внутренние парам., Q-внешнее воздействие.

А) статистические (изучают установившиеся состояния объектов в опред.момент времени) и динамические (изучают переходные пр-сы в системах либо поведение системы во времени)

Б) стахостические (отображают случайные пр-сы в объекте или же случайные воздействия на объект) и детерминированные (без случайных воздействий)

В) дискретные (описывают процессы, к-е происходят в некоторые замкнутые моменты времени) и непрерывные (пр-сы с непрерывным протеканием времени), дискретно-непрерывные.

Г) аналитические (необх.построение зависимости виде формул, к-я связывает параметры и элементы изучаемого объекта) и алгоритмические (связь между элементами и параметрами объекта выражается виде алгоритмов)

4. В зависимости от места, занимаемого в иерархии описаний – микромодели (пространство и время непрерывны), макромодели (непрерывно либо пр-во, либо время) и метамодели (агрегативный подход).

Требования к моделям:

1. Универсальность

2. Точность

3. Адекватность – модель должна отображать необходимые свойства объектов в некотором заданном диапазоне и должна соответствовать изучаемым системам и технолгич.задачам.

4. Удобство работы

5. Экономичность

6. Должна поддерживаться достаточная скорость работы

7. Наглядность результата

2.Физическое моделирование. Понятие подобия. Критерии подобия. Первая теорема подобия. Зависимые и независимые единицы измерения. Нахождение числа критериев подобия. Вторая теорема подобия. Третья теорема подобия.

Пусть имеется некоторый оригинал, описываемый как некая ф-ция от некоторого набора параметров , и модель, описываемая как . Если для всех параметров x_i выполняются соотношения, , то говорят, что объект и модель подобны. Это означает, что, исследуя свойства модели, можно перенести полученные результаты на объект, пересчитав все параметры с помощью масштабов m_i.

Проблема заключается в том, что не все m_i могут принимать независимые значения, поскольку среди параметров X есть взаимосвязанные, например, физическими законами. Простейший случай I=U/R, тогда m_i=m_U/m_R. Поэтому из трех величин произвольно могут быть выбраны только две.

Правило выбора масштабных соотношений определяет теория подобия, в основе которой лежат три теоремы.

Тогда под подобием понимают такое взаимооднозначное соответствие между параметрами модели и объекта, при котором правила перехода (критерии подобия) от X i_м к X i₀ известны.

Первая теорема подобия (теорема Ньютона-Бертрана): подобные явления имеют определенные сочетания параметров, называемые критериями подобия (π), численно одинаковые.

Проиллюстрируем примеры следующими примерами: пусть имеем механические поступательные системы, подчиняющиеся второму закону Ньютона:

Согласно второму закону Ньютона они описываются уравнениями вида:

F1-M1a1=0

F2-M2a2=0

M₁=m_M·M₂; x₁=m_x·x₂; t₁=m_t·t₂ – тогда уравнения примут следующий вид:

Произвольно введем масштабные коэффициенты:

M1=mM·M2 F1=mF·F2

x1=mx·x2 t1=m1·t2

Подставляя полученные соотношения в уравнение (3), имеем:

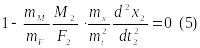
Сравнивая (4) и (5), приходим к фундаментальному соотношению для механических поступательных систем: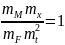

Переходя от масштаба к соответствующим физическим величинам, получаем формулировку критерия подобия Ньютона: . Оно справедливо для всех подобных механических поступательных систем.

Следствие: количество критериев подобия всегда на единицу меньше числа членов уравнения, описывающего исследуемый процесс.

Критерий Ньютона является динамическим, поскольку в него входит время.

Кроме динамических существует статистические критерии, например: для электрических цепей, подчиняющихся закону Ома, имеем:.

Вторая теорема подобия: всякое полное уравнение физического процесса, записанное в определенной системе единиц измерения, может быть представлено функциональной зависимостью критериев подобия.

Полным уравнением будем называть уравнение, в которое входят все интересующие нас в данном случае физические величины.

Системой единиц измерения называется совокупность определенным образом установленных единиц измерения, физических величин, которая включает основные (первичные), производные (вторичные) и дополнительные единицы измерения.

Основные единицы измерения выбираются произвольно!

ГОСТ 8.417-81 называется «Единицы физических величин», определяет систему СИ, в которой введено семь основных единиц:

- длина, L. м; масса, M, кг; время, T, с; сила электрического тока, I, А; термодинамическая температура, Θ, К; количество вещества, N, моль; сила света, J, кд.

Дополнительными единицами являются радиан и стерадиан.

Производные единицы измерения выражаются через основные с помощью формул размерности, которые отражают те или иные физические законы, например: из второго закона Ньютона следует формула размерности вида f=ma; [f]=[M]¹[L]¹[T]^-2=кг·м·с^-2=Н.

Аналогично устанавливаются единицы измерения для электрических величин:

- потенциал, разность потенциалов, напряжение, Вольт [B]=[L]²[M]¹[T]^-3[I]^-1;

- емкость, Фарада [Ф]=[L]^-2[M]^-1[T]⁴[I]²;

- сопротивление, Ом [Ом]=[L]²[M]¹[T]^-3[I]^-2;

- индуктивность, Генри [Гн]=[L]²[M]¹[T]^-2[I]^-2.

Группой независимых параметров объекта (процесса) называется такая группа, в которой размерность ни одного параметра не может быть получена из размерностей других параметров. Например, параметры m (масса), x (перемещение), υ (скорость) образуют группу независимых параметров, а группа m, f, a является группой зависимых параметров →f-ma=0.

Тогда некий объект (процесс) можно описать функциональной зависимостью бита O=f(x₁,x₂,…,x_k,x_k+1,…,x_m), где x₁,…,x_k – независимые параметры, а x_k+1,…,x_m – зависимые. Тогда количество критериев подобия будет равно m-k, т.е. будем иметь π₁,π₂,…, π_m-k, а k=rankA, A – матрица, образованная в формулу размерности для параметров x₁,x_m. Рангом матрицы называется наибольший порядок определителя отличного от нуля.

В результате , где α_i – целочисленная степень.

Критерии определяются следующим образом: разделим параметр на группы независимых и зависимых. Независимыми являются i,R,T; зависимыми являются L,U. Тогда в конечном итоге имеем:

. Причем ,

В результате формальная запись теоремы принимает вид: O=f(1,1,1,π₁,π₂).

Итог: таким образом, первая теорема вводит само понятие критерия подобия как безмерной величины, связывающих физические параметры объекта или процесса. Вторая теорема дает формальную процедуру для определения количества и конкретного вида критериев подобия, используя понятие формулы размерности.

Третья теорема подобия (теорема Кирпичева-Гухмана): необходимым и достаточным условиями для создания подобия явля­ются: а) пропорциональность сходственных параметров, входящих в условия однозначности; б) равенство критериев подобия сопостав­ляемых явлений (процессов).

Для примера рассмотрим электрическую схему из последова­тельно соединенных источника э.д.с. U, ключа Кл, емкости С, индуктивности L и сопротивления R (рис. 2.4).

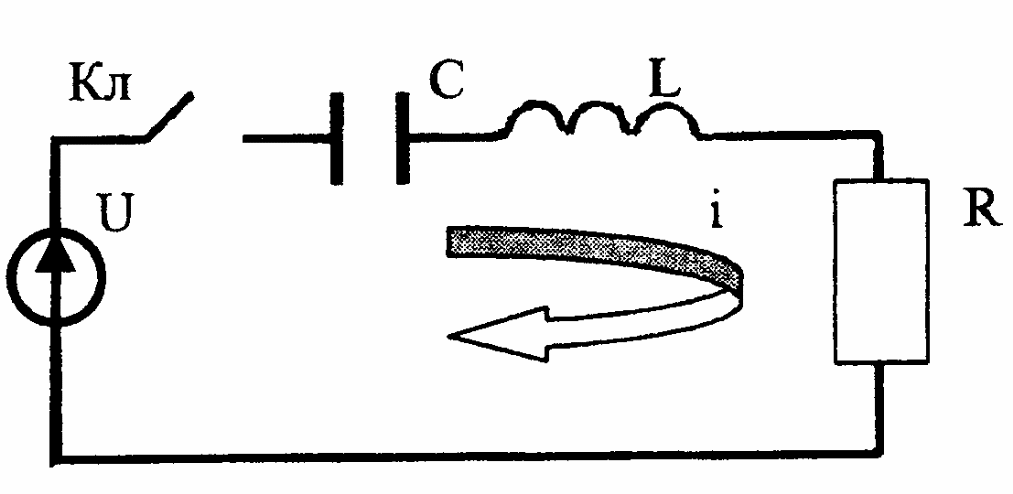
Процессы в схеме описываются уравнением вида

В данном случае имеем m=6 физических величин (параметров): L, C, R, U, I, t

Из второй теоремы подобия следует, что к = 3, т.е. число критериев подобия m-k = 3.

При выборе π₁=(i*t)\(U*C), π₂=(R*C)/t, π₃ = (L*C)/t² группы независмых параметров получаем

Тогда для двух произвольных систем такой структуры справедливы соотношения вида:

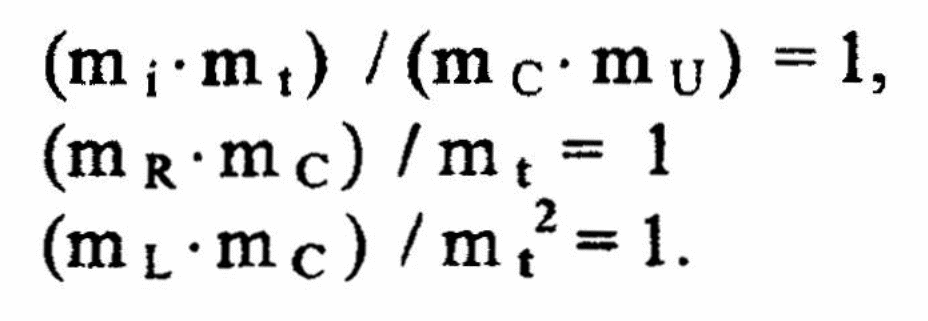
из которых следуют выражения для определения масштабов:

Для независимых переменных U, С, t соответствующие масштабы (m_U,m_C,m_t) выбираем произвольно.

Тогда для зависимых переменных L, R, i масштабы вычисляются из π₁,π₂,π₃