23.Функцияларға арифметикалық амалдар. Бүтін және рационал функциялар

f,g : R→R

D_f, D_g – анықталу облыстары

Егер D_f∩ D_g ≠Ø, онда

f+g: R →R

f-g: R →R

f*g: R →R

f/g: R →R

Егер x∈ D_f∩ D_g

1. (f+g)(x) = f(x)+g(x)

2. (f-g)(x) = f(x)-g(x)

3.(f*g)(x) = f(x)*g(x)

4. (f/g)(x) = f(x)/g(x), g(x)≠0

1,2,3 – сақиналық амалдар

1,2,3,4 – арифметикалық амалдар

α€R (αf)(x)=α*f(x)

((f+g)h)(x)=(f(x)+g(x))h(x)=f(x)*h(x)+g(x)*h(x)=(f*h+g*h)(x)

(f, D_f, E_f) (g, D_g, E_g)

(f+g, D_f+g, E_f+g)

(f-g, D_f-g, E_f-g)

(f*g, D_f*g, E_f*g)

(f/g, D_f/g, E_f/g)

(αf, D_αf, D_αg)

24. Бір жақты шектер және олар туралы теорема. f функциясы (с,d] жарты интервалда (мүмкін а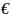 (с,d] нүктесінде де) анықталған дейік.

Анықтама 1: Егер а санына жинақталатын кез келген {x_n}, мұндағы x_n <a, n€N, тізбегіне f функциясы мәндерінің сәйкес {f(x_n)} тізбегі А санына жинақталатын болса, онда А саны х-тің а-ға ұмтылғандағы f функциясының сол жақты шегі деп аталады және былай жазылады:

A=

(Символдар арқылы: A= х_n<a (n€N) x_n →a →A )

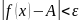Анықтама2: Егер кез келген үшін оған тәуелді саны табылып , a- теңсіздігін қанағаттандыратын барлық х үшін теңсіздігі орындалса, онда А саны х-тің а-ға ұмтылған f функциясының сол жақты шегі деп аталады және былай жазылады А=

1 және 2 – анықтамалардың мәндестігін 1-пунктегідей дәлелдеуге болады. Жоғарыда келтірілген анықтамаларға ұқсас түрде х-тің а-ға ұмтылғандағы f функциясының оң жақты шегінің 1 және 2 анықтамаларын тұжырымауға болады. Ол шекті 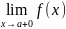арқылы белгілеп, символдар арқылы жазып көрсетейік.

1. A= х_n>a (n€N) │ x_n → a →A

2. A=

Егер а=0 болса , онда х орнына х деп, ал х→0+0 орнына х→+0 деп жазады.

25. Монотонды функциялар және олардың шектері

f(x)=x²- монотонды функцияға жатпайды.

Егер x₁<x₂ болғанда f(x₁)≤ f(x₂) болса, онда f функциясы кемімелі емес.

Егер x₁<x₂ болғанда f(x₁)≥f(x₂) болса, онда f функциясы өспелі емес.

x₁< x₂ => f(x₁)< f(x₂) => f – өспелі.

x₁< x₂ => f(x₁)> f(x₂) => f – кемімелі. Осылардың бәрі монотонды функиялар.

Теорема 2.1.9. (а, b) интервалында f функциясы монотонды болсын және α=inff(x), β=sup f(x), a<x<b.

(a) Егер f кемімелі емес болса, онда f(а⁺)=α және f(b^-)=β

(b) Егер f өспелі емес болса, онда f(а⁺)= β және f(b^-)= α

a⁺=-∞, егер а=-∞

b^-=+∞, егер b=+∞

(c)Егер а<x₀<b болса, онда f(x₀⁺) және f(x₀^-) табылады және олар арқылы: Сонымен бірге f функциясы кемімелі емес болса, онда f(x₀^-)≥ f(x₀) ≥ f(x₀⁺), ал өспелі емес болса, онда f(x₀^-)≥ f(x₀) ≥ f(x₀⁺).

26. Шенелген функциялар. Төменгі және жоғарғы шектер.

f функциясы шенелген деп атаймыз, егер ∀ х ∈ D_f үшін │f(x)│<М болатындай М< ∞ табылса.

-M≤ f(x)≤М

[a, x₀), x₀< ∞, x₀= ∞, x∈ [a, x₀), S_f(x; x₀)=supf(t), x≤t≤x₀

[a x t ) ^X0

S_f: x=>supf(t), x≤t<x₀

I_f(x;x₀)=inf f(t), x≤t<x₀

(0-жоғарғы шек)

(0-төменгі шек)

Шенелген функциялар. Төменгі және жоғарғы шектер

f:S→ R, S≤R

ƎM∈R, M< ∞ және ∀x∈S үшін │f(x)│≤М, онда f функциясы S жиынында шенелген.

Анықтама:2.1.10. f функциясы [а,х₀) аралығында шенелсін, x₀≤∞

∀x€ [a,x₀); S_f(x,x₀)=supf(t); x≤t≤x₀

өспейтін функция монотонды

I_f(x,x₀)=inf f(t), x≤t<x₀

Кемімейтін функция монотонды

Теорема 2.1.11 (жоғарғы шек үшін)

Егер f функциясы [a, x₀) аралығында шенелген болса, онда β=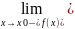

саны Ǝ және ол келесі қасиеттерге ие жалғыз ғана нақты сан.

(а) Егер ε>0, онда а₁<x<x₀ болғанда f(x)<β+ε болатындай a₁∈ [a, x₀) саны табылады.

(b) Егер ε>0 және a₁∈ [a, x₀), онда қандай да бір х∈ [a, x₀) үшін f(x)>β-ε

Теорема 2.1.12 (төменгі шек үшін )

Егер f функциясы [a, x₀) аралығында шенелген болса, онда α= саны табылады және ол келесі қасиеттерге ие жалғыз ғана нақты сан.

(а) Е>0 a₁≤x< x болғанда f(x)>α-ε болатындай а₁ саны Ǝ.

(b) Егер ε>0 және a₁∈ [a, x₀) онда қандай да бір x∈ [a, x₀) үшін f(x)<α+ε.