20.Жиындардың декарттық көбейтіндісі. Сәйкестік, кері сәйкестік. Сәйкестіктер суперпозициясы.

f;R→R

N,M-жиындар

N жатады n;M тиісті m

FтиістіN*M,F N жиынынан М жиынына қарай анықталған сәйкестік

Сәйкестік-баратын жиын мен шығатын жиынның тік көбейтіндісінің қандайда бір ішкі жиыны

F=N*M-универсал сәйкестік

N=M,F iшкі жиыны N*M-N жиынында анықталған екі орынды қатынас

F ішкі жиыны N. F-бір орынды қатынас

G*F={(m,k)тиісті N*K│табылады m жатады M(n,m);тиісті F(m,k)тиістіG}-супер позизицисы

F сәйкестігі мен Gсәикстігініңсупер позициясы

Үш сәйкестіктің суперпозициясы ассоциативті заңға бағынады

Егер (n1n2)(m1m2) F болғанда m1=m2 болса,онда F функционалды сәйкестік

Д(F)=Nболса,онда F ішкі жиын N*Mфункциональды сәикестігі функция деп аталады

Егер n1 →f(n1) f(n2)болса онда f:N→M функциясы иньюктивті

f:N→M функциясы сюрьективті деп аталады

f:N→M функциясы бір мезгілде иньективті және сюрективті болса,онда f биективті

21.Функционалдық сәйкестік. Функция,анықталу облысы, мәндер жиыны.

сәйкестік

Егер , болғанда болса, онда F функционалды сәйкестік.

Берілген х айнымаланың әрбір мәніне белгілі заң немесе ереже бойынша у айнымалысының анықталған бір-ақ мәні сәйкес келіп отырса, у шамасы х айнымалысының функциясы д.а. х – тәуелсіз айнымалы н/е аргумент, у – тәуелді айнымалы н/е функция.

Функция белгіленуі:

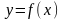, , , , т.б.

Мұндағы ,… аргумент -тің берілген мәні бойынша -тің сәйкес мәні қалай табылатынын көрсететін заңды немесе ережені бейнелейді.

Е және F жиындары берілсін. Е жиынының әрбір элементіне F жиынының бір ғана элементін сәйкес қоятын ереже функция д.а. Бұл ережені сәйкестік, тәуелділік деп те атайды.

Жиындардың элементтерін белгілеу үшін символдар қолданылады. Е жиынының кез – келген элементін бейнелейтін символ тәуелсіз айнымалы немесе функцияның аргументі д.а. Осыған орай, тәуелсіз айнымалыға н/е аргументке сәйкес элементті белгілейтін символ тәуелді айнымалы д.а.

Функция анықталған және ақырлы нақты мәндер қабылдайтын тәуелсіз айнымалының барлық мәндерінің жиыны сол функцияның анықталу облысы, ал тәуелді айнымалының барлық мәндерінің жиыны функцияның мәндер жиыны д.а.

Е – функцияның анықталу облысы, ал F – функцияның мәндер жиыны.

Егер F – нақты сандардан құралған жиын болса (Е – кез-келген жиын), онда функциясын нақты мәнді н/е санды функция д.а.

Егер жиындар теңдігі орындалса, яғни жиынының әрбір элементі функциясынынң мәні болса, онда - сюрьективті функция д.а. Мысалы, үшін болғанда функциясы сюрьективті болады да, функциясы сюрьективті емес.

Егер 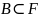болса, үшін бос н/е бір элементті болса, онда -ті иньективті функция д.а.

Егер , 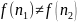болса, онда функциясы иньективті д.а.

Егер функциясы үшін әрбір 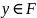элементі функциясының мәні болып, тек қана бір нүктеде қабылданса, онда биективті функция д.а. Әрине, биективті болу үшін, ол сюрьективті және иньективті болуы қажетті және жеткілікті.

және g функциялары бойынша анықталған сәйкестігі, яғни әрбір элементіне бойынша сәйкес келетін элементіне g тәртібін қолданудың нәтижесін сәйкес қоятын ереже, және g функцияларының композициясы н/е күрделі функция д.а. да, н/е символдарымен белгіленеді.