
- •Өрістегі арифметикалық амалдардың қасиеті. Ерекше элементтер, қарама-қарсы элементтер, кері элементтер.
- •Реттік қатынас. Көбейту және қосу амалдарымен байланысы. Реттелген өрістер.
- •4. Санның абсолюттік шамасы. Үшбұрыш теңсіздігі. Оның салдары.
- •5. Жиынның жоғарғы жағы. Жоғарыдан шенелген жиын. Супремум.
- •6. Жиын супремумының қасиеттері туралы теорема.
- •7. Архимед қасиеті. Жиынның тығыздылығы.
- •8. Рационал сандар және иррационал сандар жиындарының нақты сандар жиынындағы тығыздығы.
- •10.Жиынның инфимумы қасиеттері туралы теорема.
- •12. Пиано постулаттары және математикалық индукция принципі.
- •13.Ішкі жиын, жиындар теңдігі. Жиындарға алу, бірігу және қиылысу амалдары. Толықтауыш.
- •14.Маңай, ішкі нүкте, жиынның іші. Ашық жиын.
- •15. Ашық жиындардың бірігуі туралы теорема.
- •16. Тұйық жиын. Тұйық жиындардың қиылысуы туралы теорема.
- •18. Ашық жабу. Гейне-Борель теоремасы.
- •19) Больцано-Вейерштерн теоромасы:
- •20.Жиындардың декарттық көбейтіндісі. Сәйкестік, кері сәйкестік. Сәйкестіктер суперпозициясы.
- •21.Функционалдық сәйкестік. Функция,анықталу облысы, мәндер жиыны.
- •22. Функциялардың шектері. Анықтамасы және қасиеті.
- •23.Функцияларға арифметикалық амалдар. Бүтін және рационал функциялар
- •25. Монотонды функциялар және олардың шектері
- •26. Шенелген функциялар. Төменгі және жоғарғы шектер.
- •27. Үзіліссіздіктің маңайлар бойынша анықтамасы. Біржақты үзіліссіздіктер
- •28. Кесек үзіліссіздік. Үзілістілік, айырым (секіру). Жойылатын үзілістіліктер.
- •29) Үзiлiссiз функцияларға қолданылатын арифметикалық амалдар
- •30)Монотонды функцияның үзіліссіздігі. Керi функция ұғымы
- •31. Үзіліссіздік және бірқалыпты үзіліссіздік.
- •33.Туынды және оның интерпретациясы. Жанама.
- •34) Дифференциялдау және арифметикалық амалдар.
- •35. Күрделі функцияның туындысы. Кері функцияның туындысы.
- •36. Біржақты туындылар. Туындының бар болуы.
- •37. Функцияның экстремум мәндері. Олардың қажетті шарты.
- •38. Ролль теоремасы.
- •39. Туындының аралық мәні туралы теорема.
- •42. Лопиталь ережесі. Анықталмағандықтар.
- •43) Тейлор теоремасы
- •44. Тейлор теоремасын локальді экстремумға қолдану. (негізі: Тейлордың локальдық формуласын экстремумға қолдану)
- •46.Дифференциалданатын функцияның үзіліссіздігі. Дифференциалданбайтын фукцияның үзіліссіздігі.
- •48. Монотонды функцияның үзіліссіз болуы туралы критерий.
- •49. Үзіліссіз және бірқалыпты үзіліссіз емес функцияның мысалы
- •50. Үзіліссіз функциялар үшін кері функцияның бар болуы туралы теорема.
- •Реттік қатынас. Көбейту және қосу амалдарымен байланысы. Реттелген өрістер.
- •Санның абсолюттік шамасы. Үшбұрыш теңсіздігі. Оның салдары.
- •Жиынның жоғарғы жағы. Жоғарыдан шенелген жиын. Супремум.
18. Ашық жабу. Гейне-Борель теоремасы.
H={h тиісті R};Sтиісті R
S тиісті бірігу ,онда h титисті H
H S тің жабуы
S=[2,3]
H={(1,2),(2,2,5),(2,5,3)}
S тиісті h, Uh2Uh3U…Uh4
H={h1,h2,hn} Sтің жабуы
Ашық жабу H={h R/h ашық жиын }
Егер H Sтің жабуы болса,онда H ашық жабу
Теорема. Егер Hтұйық шенелген нақты сандардың Sжиынының ашық жабуы болса,ондаS арқылы мөлшерлі(Sарқылы)H ашық жабушыға ие болады.
Гейне анықтамасы
а нүктесі қандай болмасын (c,d) маңайында анықталған f функциясын қарастырайық.
Анықтама:
Егер а саны жинақталатын кез келген
{ }
тізбегі үшін f функциясы мәндерінің
сәйкес { f {
}}
тізбегі А санына жинақталатын болса,
онда А санын f функциясының х-тің а-ға
ұмтылғандағы шегі деп аталады
A=lim┬(n→∞)f(x).Символдар
арқылы жазатын болсақ
(A=lim┬(n→∞)〖f(x)〗⟺∀{
},
≠a|x_n→a⇒f(
)→A,
nϵN)
}
тізбегі үшін f функциясы мәндерінің
сәйкес { f {
}}
тізбегі А санына жинақталатын болса,
онда А санын f функциясының х-тің а-ға
ұмтылғандағы шегі деп аталады
A=lim┬(n→∞)f(x).Символдар
арқылы жазатын болсақ
(A=lim┬(n→∞)〖f(x)〗⟺∀{
},
≠a|x_n→a⇒f(
)→A,
nϵN)
Анықтама: ( Гейне бойынша) Егер – ге жинақталатын -ден өзгеше Х аргументінің мәндерінің бірінші тізбегі сәйкесінше функция мәндерінің екінші тізбегі а санына жинақталса, онда а саны f(x) функциясының нүктесіндегі шегі деп аталады. lim┬(х→ )〖f(x)=a〗
19) Больцано-Вейерштерн теоромасы:
Әрбір шенелген ақырсыз нақты сандар жиыны ең болмағанда бір шектік нүктеге ие. Әрбір шенелген шектік нүктеге ие емес жиын арқылы. Вейерштрастың бiрiншi теоремасы
Егер
f(x) [a, b]-да анықталған және үзіліссіз
болса, онда ол шектеледі. Яғни, тұрақты
және шектеулі m және M табылып, a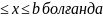 m
m
 f(x)
M болады.
f(x)
M болады.
Д/у:
Кері жорып, f [a;b] шектелмесін. Онда[a;b]
n N
болатындай хn
нүктесі
табылады |f(хn)|
N
болатындай хn
нүктесі
табылады |f(хn)| n
(1)болатындай. Енді осы хn
тізбектен
n
(1)болатындай. Енді осы хn
тізбектен
 бөліп алуға болады және оның шегі
бөліп алуға болады және оның шегі
 =
=
және
a b
болады. f үзіліссіз болғандықтан
=
b
болады. f үзіліссіз болғандықтан
= ,
ал бұл мүкін емес, себебі (1) теңсіздік
бойынша
,
ал бұл мүкін емес, себебі (1) теңсіздік
бойынша

 ,Яғни кері жорығанымыз дұрыс емес.
Теорема дәлелденді.
Вейерштрастың екiншi теоремасы
,Яғни кері жорығанымыз дұрыс емес.
Теорема дәлелденді.
Вейерштрастың екiншi теоремасы
Егер f(x) [a, b]-да анықталған және үзіліссіз болса, онда ол бұл аралықта өзінің дәл жоғарғы және дәл төменгі шекарасына жетеді.
Дәлелдеу.
f(x) [a, b] –да үзіліссіз болғандықтан,
Вейерштрастың 1-теоремасы бойынша ол
шенелген, яғни сәйкесінше f(x)-тің [a,
b]-да дәл жоғарғы M және дәл төменгі m
шекаралары болады. M-нің бар болатынын
көрсетейік.
 x
[a,
b], f(x1)
= M.
x
[a,
b], f(x1)
= M.
Кері жориық.
[a,
b]-да M-ге тең f(x)-тің ешбір мәні табылмасын:
 x
[a,
b],
f(x)
x
[a,
b],
f(x)
 M. Онда кез келген x
[a,
b] үшін f(x)
M орынды. [a, b]-да кез келген F(x) =
M. Онда кез келген x
[a,
b] үшін f(x)
M орынды. [a, b]-да кез келген F(x) =
 барлық аралықта оң. F(x) рационал болып
табылады. Бұл жағдайда f(x) шенелген,
яғни
x
[a,
b] үшін
µ>0
және F(x)
µ , бұдан f(x)
M – 1/ µ . Сонымен M – 1/ µ саны M-нен кіші
және [a, b]-да f(x)-тің жоғарғы шекарасы
болып табылады. Бірақ бұл M саны дәл
жоғарғы нүкте екендігіне қайшы бұл
қайшылықтан f(x1)
= M болатындай x1
[a,
b] бар болатындығы дәлелденеді. Ұқсасынша
f(x) [a,b]-да өзінің дәл төменгі шекарасына
жететіндігі дәлелденеді. Үзіліссіз
f(x)-тің (a, b)-дағы дәл жоғарғы және дәл
төменгі шекаралардың айырмасы ω = M –
m f(x)-тің осы аралықтағы тербелісі деп
аталады.
барлық аралықта оң. F(x) рационал болып
табылады. Бұл жағдайда f(x) шенелген,
яғни
x
[a,
b] үшін
µ>0
және F(x)
µ , бұдан f(x)
M – 1/ µ . Сонымен M – 1/ µ саны M-нен кіші
және [a, b]-да f(x)-тің жоғарғы шекарасы
болып табылады. Бірақ бұл M саны дәл
жоғарғы нүкте екендігіне қайшы бұл
қайшылықтан f(x1)
= M болатындай x1
[a,
b] бар болатындығы дәлелденеді. Ұқсасынша
f(x) [a,b]-да өзінің дәл төменгі шекарасына
жететіндігі дәлелденеді. Үзіліссіз
f(x)-тің (a, b)-дағы дәл жоғарғы және дәл
төменгі шекаралардың айырмасы ω = M –
m f(x)-тің осы аралықтағы тербелісі деп
аталады.
