13.Ішкі жиын, жиындар теңдігі. Жиындарға алу, бірігу және қиылысу амалдары. Толықтауыш.

Өзара бөлек заттарды біріктіріп , бүтін бір заттай қарастыруға болады . Сол жаңа зат жиын деп, ал оның құрамындағы заттардың әрқайсысы жиынның элементі деп аталады.

Егер Р әрпімен белгілі бір қасиетті қабылдайтын заттардың бәрінен құрылған жиын

(1) символымен белгіленеді.

Егер Р қасиетін бірде-бір зат қабылдамаса, онда (1) жиынын бос жиын дейді де, символымен белгілейді.

Жиындардың теңдігі. Кірістіру символы бойынша жиындардың теңдігі анықталады. Егер Е және F жиындары үшін және кірістірулері бірдей орындалса, яғни бірінің кез-келген элементі екіншісінде жатса, онда Е және F жиындары тең дейді де, E=F символымен белгілейді.

Жиындардың қиылысуы. Е және F жиындарының қиылысуы деп жиынын, яғни Е мен F жиындарында бірдей жататын x элементтерінен құрылған жиын аталады. Егер ондай элементтер болмаса, онда

Жиындарды бірігуі. Е және F жиындардың біріктіруі деп жиынын, яғни Е және F жиындарының кемінде біреуінде жатқан элементтерінен құрылған жиынды атайды (бұған Е және F–те қатар жататын элементтер де кіреді)

Жиындардың айырымы. Е және F жиындарының айырымы деп жиыны, яғни Е жиынында жатып, F жиынында жатпайтын x элементтерінің жиыны аталады. Әрине, болған жағдайда жиын болады.

14.Маңай, ішкі нүкте, жиынның іші. Ашық жиын.

ашық интервал

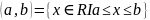
1. Жартылай шексіз интервалдар

2. Шексіз интервал

Маңай: - нүктесінің маңайы. нүктесі өзінің қандай да бір маңайымен бірге S-ке тиісті болса, онда S жиынының ішкі нүктесі.

R ішкі жиынының барлық нүктелері, ішкі нүктелері болса, онда S ашық жиын деп аталады.

S R-дің ішкі жиыны, барлық нүктелері ішкі нүктелер болса S ашық жиын деп аталады.

Кез-келген х жатады S нүктесі үшін табылады ἐ>0; (х-ἐ,х+ἐ)ішкі жиыны S-тің

a<y<x<z<b

ἐ=min{x-y,z-x}

ἐ=min{x-a,b-x}

Теорема,Ашық жиындардың бірігуі ашық жиын болады.Тұйық жиындардың қиылысуы тұйық деп аталад G-ашық жиындардың жиыны

G={g ішкі нүктесі ;g-ашық}

S=бірігуі g g жатады G

Кез-келген х жатады S табылады g жатады G;табылады ἐ>0;(x-ἐ,x+ἐ)

x S-тің ішкі нүктесі ;S-ашық жиын

15. Ашық жиындардың бірігуі туралы теорема.

S R-дің ішкі жиыны, барлық нүктелері ішкі нүктелер болса S ашық жиын деп аталады.

Кез-келген х жатады S нүктесі үшін табылады ἐ>0; (х-ἐ,х+ἐ)ішкі жиыны S-тің

a<y<x<z<b

ἐ=min{x-y,z-x}

ἐ=min{x-a,b-x}

Теорема,Ашық жиындардың бірігуі ашық жиын болады.Тұйық жиындардың қиылысуы тұйық деп аталад G-ашық жиындардың жиыны

G={g ішкі нүктесі ;g-ашық}

S=бірігуі g g жатады G

Кез-келген х жатады S табылады g жатады G;табылады ἐ>0;(x-ἐ,x+ἐ)

x S-тің ішкі нүктесі ;S-ашық жиын

16. Тұйық жиын. Тұйық жиындардың қиылысуы туралы теорема.

Егер S-тің толықтауышы ашық болса,онда S тұйық жиын деп аталады.

[a,b]ᶜ=(-∞,a)бірігуі (в,∞)-ашық ,ендеше[а,в]тұйық жиын ;[a,b) x=a кез-келген ἐ>0 (х-ἐ,х+ἐ)ішкі жиыны емес[a,b)ашық емес.

Теорема,Тұйық жиындырдың қиылысуы тұйық болады.Ашық жиындардың бірігуі ашық жиын болады.

F-тұйық жиын

F={f R-дің ішкі жиыны, f-тұйық жиын}

f F-тің ішкі жиыны

Sᶜ=(бірігу f)ᶜ=бірігу fᶜ -ашық

Sᶜ=ашық,S-тұйық

G-ашық жиындардың жиыны

G={g ішкі нүктесі ;g-ашық}