
- •Өрістегі арифметикалық амалдардың қасиеті. Ерекше элементтер, қарама-қарсы элементтер, кері элементтер.
- •Реттік қатынас. Көбейту және қосу амалдарымен байланысы. Реттелген өрістер.
- •4. Санның абсолюттік шамасы. Үшбұрыш теңсіздігі. Оның салдары.
- •5. Жиынның жоғарғы жағы. Жоғарыдан шенелген жиын. Супремум.
- •6. Жиын супремумының қасиеттері туралы теорема.
- •7. Архимед қасиеті. Жиынның тығыздылығы.
- •8. Рационал сандар және иррационал сандар жиындарының нақты сандар жиынындағы тығыздығы.
- •10.Жиынның инфимумы қасиеттері туралы теорема.
- •12. Пиано постулаттары және математикалық индукция принципі.
- •13.Ішкі жиын, жиындар теңдігі. Жиындарға алу, бірігу және қиылысу амалдары. Толықтауыш.
- •14.Маңай, ішкі нүкте, жиынның іші. Ашық жиын.
- •15. Ашық жиындардың бірігуі туралы теорема.
- •16. Тұйық жиын. Тұйық жиындардың қиылысуы туралы теорема.
- •18. Ашық жабу. Гейне-Борель теоремасы.
- •19) Больцано-Вейерштерн теоромасы:
- •20.Жиындардың декарттық көбейтіндісі. Сәйкестік, кері сәйкестік. Сәйкестіктер суперпозициясы.
- •21.Функционалдық сәйкестік. Функция,анықталу облысы, мәндер жиыны.
- •22. Функциялардың шектері. Анықтамасы және қасиеті.
- •23.Функцияларға арифметикалық амалдар. Бүтін және рационал функциялар
- •25. Монотонды функциялар және олардың шектері
- •26. Шенелген функциялар. Төменгі және жоғарғы шектер.
- •27. Үзіліссіздіктің маңайлар бойынша анықтамасы. Біржақты үзіліссіздіктер
- •28. Кесек үзіліссіздік. Үзілістілік, айырым (секіру). Жойылатын үзілістіліктер.
- •29) Үзiлiссiз функцияларға қолданылатын арифметикалық амалдар
- •30)Монотонды функцияның үзіліссіздігі. Керi функция ұғымы
- •31. Үзіліссіздік және бірқалыпты үзіліссіздік.
- •33.Туынды және оның интерпретациясы. Жанама.
- •34) Дифференциялдау және арифметикалық амалдар.
- •35. Күрделі функцияның туындысы. Кері функцияның туындысы.
- •36. Біржақты туындылар. Туындының бар болуы.
- •37. Функцияның экстремум мәндері. Олардың қажетті шарты.
- •38. Ролль теоремасы.
- •39. Туындының аралық мәні туралы теорема.
- •42. Лопиталь ережесі. Анықталмағандықтар.
- •43) Тейлор теоремасы
- •44. Тейлор теоремасын локальді экстремумға қолдану. (негізі: Тейлордың локальдық формуласын экстремумға қолдану)
- •46.Дифференциалданатын функцияның үзіліссіздігі. Дифференциалданбайтын фукцияның үзіліссіздігі.
- •48. Монотонды функцияның үзіліссіз болуы туралы критерий.
- •49. Үзіліссіз және бірқалыпты үзіліссіз емес функцияның мысалы
- •50. Үзіліссіз функциялар үшін кері функцияның бар болуы туралы теорема.
- •Реттік қатынас. Көбейту және қосу амалдарымен байланысы. Реттелген өрістер.
- •Санның абсолюттік шамасы. Үшбұрыш теңсіздігі. Оның салдары.
- •Жиынның жоғарғы жағы. Жоғарыдан шенелген жиын. Супремум.
10.Жиынның инфимумы қасиеттері туралы теорема.
Жиынның инфимумы
R нақты сандар жиыны берілсін
X R жиынының төменгі шекаралар жиынының ең үлкен элементі Х жиынының дәл төменгі шекарасы деп аталады да, infX немесе inf{x} арқылы белгіленеді және инфимумХ деп окылады (лат: infimum – ең төменгі).
Сонымен,
![]() саны X жиынының супремумы болуы үшін
келесі екі шарт орындалуы керек:
саны X жиынының супремумы болуы үшін
келесі екі шарт орындалуы керек:
саны X жиынының төменгі шекарасы,яғни
 үшін
үшін  болады
болады саны X жиынының жоғарғы шекараларының
ең үлкені, яғни
санынан үлкенболатын әрбір
саны X жиынының жоғарғы шекараларының
ең үлкені, яғни
санынан үлкенболатын әрбір  саны X жиынының төменгі шекарасы бола
алмайды.Басқа сөзбен айтқанда,
саны X жиынының төменгі шекарасы бола
алмайды.Басқа сөзбен айтқанда,
 теңсіздігін
қанағаттандыратын кез келген
теңсіздігін
қанағаттандыратын кез келген  саны үшін
саны үшін
![]() теңсіздігі орындалатын
теңсіздігі орындалатын ![]() саны табылады.
саны табылады.
Супремумның анықтамасы кванторлар тілінде былай жазылады:
1.![]()
2.![]()
![]() санынан
кіші болатын кез келген
саны
санынан
кіші болатын кез келген
саны ![]() түрінде бейнеленеді, сондықтан, 2 шартты
былай жазуға да болады:
түрінде бейнеленеді, сондықтан, 2 шартты
былай жазуға да болады:
![]()
Әрине, R жиынының ең кіші элементі бар болса онда ол R–дің инфимумы болады.
11. Нақты сандар жиынының кеңеюі. Анықталмағандықтар.
1. Натурал сандар
Натурал сандар деп мына сандарды атаймыз 0, 1, 2, 3, 4,…
Барлық натурал сандар жиының N символымен белгіленеді. Белгілі бір a санының натурал сан екенің көрсету үшін a ∈ N деп белгілейміз. Мысалы 1 ∈ N, 5 ∈ N, 3 ∈ N.
2. Бүтін сандар
Бүтін сандар деп оң және теріс таңбасымен алынған барлық натурал сандар жиынынан құралған сандар жиының атаймыз.
Яғни бүтін сандар 0, 1, 2, 3, 4,… және -1, -2, -3, -4,… сандар жиындарының бірігуінен құралған. Бүтін сандар жиының P символымен белгілейміз.
Тұжырым.
N жиынына еңетің кез келген сан P жиынына да еңеді. Бұндай жағдайда N жиыны P жиынына еңеді дейді, және N ⊆ P деп жазады.
Рационал сандар
Рационал сандар деп a/b (a ∈ P, b ∈ P, b ≠ 0) сандарын атаймыз. Мысалы 1/3 , 10/7. Рационал сандар жиының R деп белгілейміз.
Кез
келген бүтін c саны
рационал жиынына еңеді да, яғни рационал
саны да болып табылады. Өйткені ![]() ,
соңдықтан P ⊆ R.
,
соңдықтан P ⊆ R.
4. Иррационал сандар
Иррационал
сан деп
π = 3,141592… немесе ![]() =
1,4… сандары тәрізді бөлшек бөлігі
шексіз, периодты емес цифрлардан
құралған сандарды атаймыз.
=
1,4… сандары тәрізді бөлшек бөлігі
шексіз, периодты емес цифрлардан
құралған сандарды атаймыз.
Иррационал сандар жиының Q деп белгілейміз.
5. Нақты сандар
Нақты сандар жиыны деп барлық- натурал, бүтін, рационал және иррационал сандардан құралған сандар жиының атаймыз. Және бұл жиынды Z әрпімен белгілейміз.Негізгі анықталмағандықтарға мыналар жатады:
 ,
,
 ,
,
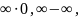

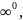
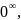

12. Пиано постулаттары және математикалық индукция принципі.
 натурал
сандар жиыны.
натурал
сандар жиыны.
(А)

(В)
Әрбір
 натурал санымен байланысқан төркіні
болатын
натурал санымен байланысқан төркіні
болатын
 жалғыз ғана сан табылады.
жалғыз ғана сан табылады.
(С)
 1-дің төркіні жоқ.
1-дің төркіні жоқ.
N –нің төркіні жоқ.
(D)
Егер

Егер төркіндері әртүрлі болса, онда олардың сандары да әртүрлі болады.
(Е) Төркіні жоқ санды немесе бүкіл төркінді қамтитын натурал сандар.

Натурал сандар жиынының анықтамасынан салдар ретінде математикалық дәлелдеулердің маңызды әдістерінің бірі – математикалық индукция әдісі шығады.
Әрбір
натурал
 үшін
үшін
 тұжырымы айтылған болсын. Әрине,кейбір
–дер үшін
орындалып, кейбір
-дер
үшін
орындалмауы да мүмкін. Бірақ, егер:
тұжырымы айтылған болсын. Әрине,кейбір
–дер үшін
орындалып, кейбір
-дер
үшін
орындалмауы да мүмкін. Бірақ, егер:
орындалса,
Әрбір натурал үшін орындалғанда де орындалса, онда тұжырымы кез келген натурал үшін орындалады.
Расында
да,
орындалатын
сандарынан
құрылған жиынды А әрпімен белгілесек,
онда
 және
және
 шарттары орындалады. Сондықтан, натурал
сандардың анықтамасы бойынша А натурал
сандар жиынының дәл өзі болады, яғни
тұжырымы
кез-келген
үшін орындалады.
шарттары орындалады. Сондықтан, натурал
сандардың анықтамасы бойынша А натурал
сандар жиынының дәл өзі болады, яғни
тұжырымы
кез-келген
үшін орындалады.
Барлық натурал сандар туралы теореманы дәлелдеген сайын, яғни тұжырымы әрбір натурал саны үшін орындалатынын дәлелдеу үшін, әрқашан да келесі, математикалық индукция әдісі деп аталатын әдісті қолдану керек : 1) мен 2) шарттарының орындалатынын тексеру керек.
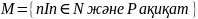
(а)
бойынша,
 және b бойынша,
және b бойынша,
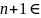 M
n
M
n болғанда. M=N.
болғанда. M=N.
