48. Монотонды функцияның үзіліссіз болуы туралы критерий.

Теорема. Егер I аралығында анықталған монотонды функциясының мәндер жиыны байланысты жиын болса, онда функциясы үзіліссіз болады. (Егер 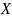нақты сандар жиынының кез келген екі элементінің арасындағы барлық сандар да сол жиында жатса, яғни арты орындалса, онда байланысты жиын д.а.)

Дәлелдеуі. Кері жорып, үзілісті делік. Анықтық үшін функциясы кемімейтін болып, нүктесінде оң жақты үзілісті болсын, яғни . Онда саны -тің I аралығындағы мәні бола алмайды, яғни барлық үшін 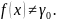Расында да, біріншіден, барлық , үшін екіншіден, монотонды функцияның шегі туралы теорема бойынша әрбір , үшін

.

Сонымен, саны функциясының екі мәнінің арасында жатып (әрбір ), өзі -тің мәні болмайды. Бұл функциясының мәндерінің жиыны байланысты екеніне қайшы келеді, демек, -тің бірде-бір үзіліс нүктесі жоқ.

49. Үзіліссіз және бірқалыпты үзіліссіз емес функцияның мысалы

Үзіліссіз ф-я мысалы:

1-мысал. -нің үзіліссіз функция екенін дәлелдеу керек.

Шынында, берілген функция сандар осінің кез-келген нүктесінде анықталған. деп шенелмеген интервалынан кез-келген бір нүкте белгілейік.Сонда, біріншіден:

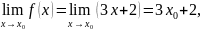
екіншіден,

Демек,

яғни, қарастырылып отырған функция нүктесінде үзіліссіз болып шықты. Ал деп интервалының кез-келген нүктесін белгілегенбіз. Сондықтан функция көрсетілген интервалдың барлық нүктелерінде үзіліссіз.

2-мысал. функ-н үіліссіздікке зерртеу.

Шешу. Функцияның анықталу облысы . Кез-келген нүктесін аламыз.

Сонда:

және

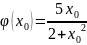
яғни,

Олай болса, ункциясы сандар осінің кез келген нүктесінде үзіліссіз.

Бірқалыпты үзіліссіз емес функция мысалы:

1-мысал. Егер функциясы белгілі бір 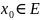нүктесінің кез келген маңайында шектелмеген болса, онда бұл функция бірқалыпты үзіліссіз емес.

Шынында да кез келген саны үшін нүктесінің маңайынан болғанымен болатын 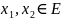нүктелері табылады.

2-мысал. функциясы бүкіл жиынында үзіліссіз, бірақ ол бұл жиында бірқалыпты үзіліссіз емес. Шынында да, , сондықтан . Ал

.

Сондықтан және кез келген үшін болғанымен болатын нүктелері табылады.

50. Үзіліссіз функциялар үшін кері функцияның бар болуы туралы теорема.

Теорема. Егер функциясы кесіндісінде үзіліссіз және өспелі (кемімелі) болса, онда оның кесіндісінде үзіліссіз және өспелі (кемімелі) кері функциясы бар.

Дәлелдеуі. Анықтық үшін функциясын кесіндісінде өспелі деп есептейік. Үзіліссіз функцияның мәндер жиыны кесіндісі болады, өйткені 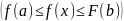және Коши теоремасы бойынша функциясы кесіндісіндегі кез-келген мәнін ең болмағанда бір ретқабылдайды. Ал функциясы кесіндісінде өспелі болғандықтан мәндер жиыны болатын кесіндісінде анықталған кері функциясы бар. Бұл функция , шынында да, теңсіздігін қанағаттандыратын кесіндісіндісінен нүктелері табылады деп ұйғарсақ, онда , яғни 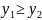теңсіздігіне келер едік. Ал бұл теңсіздігіне қайшы.

функциясы кесіндісінде үзіліссіз. Теорема дәлелденді.