
- •Өрістегі арифметикалық амалдардың қасиеті. Ерекше элементтер, қарама-қарсы элементтер, кері элементтер.
- •Реттік қатынас. Көбейту және қосу амалдарымен байланысы. Реттелген өрістер.
- •4. Санның абсолюттік шамасы. Үшбұрыш теңсіздігі. Оның салдары.
- •5. Жиынның жоғарғы жағы. Жоғарыдан шенелген жиын. Супремум.
- •6. Жиын супремумының қасиеттері туралы теорема.
- •7. Архимед қасиеті. Жиынның тығыздылығы.
- •8. Рационал сандар және иррационал сандар жиындарының нақты сандар жиынындағы тығыздығы.
- •10.Жиынның инфимумы қасиеттері туралы теорема.
- •12. Пиано постулаттары және математикалық индукция принципі.
- •13.Ішкі жиын, жиындар теңдігі. Жиындарға алу, бірігу және қиылысу амалдары. Толықтауыш.
- •14.Маңай, ішкі нүкте, жиынның іші. Ашық жиын.
- •15. Ашық жиындардың бірігуі туралы теорема.
- •16. Тұйық жиын. Тұйық жиындардың қиылысуы туралы теорема.
- •18. Ашық жабу. Гейне-Борель теоремасы.
- •19) Больцано-Вейерштерн теоромасы:
- •20.Жиындардың декарттық көбейтіндісі. Сәйкестік, кері сәйкестік. Сәйкестіктер суперпозициясы.
- •21.Функционалдық сәйкестік. Функция,анықталу облысы, мәндер жиыны.
- •22. Функциялардың шектері. Анықтамасы және қасиеті.
- •23.Функцияларға арифметикалық амалдар. Бүтін және рационал функциялар
- •25. Монотонды функциялар және олардың шектері
- •26. Шенелген функциялар. Төменгі және жоғарғы шектер.
- •27. Үзіліссіздіктің маңайлар бойынша анықтамасы. Біржақты үзіліссіздіктер
- •28. Кесек үзіліссіздік. Үзілістілік, айырым (секіру). Жойылатын үзілістіліктер.
- •29) Үзiлiссiз функцияларға қолданылатын арифметикалық амалдар
- •30)Монотонды функцияның үзіліссіздігі. Керi функция ұғымы
- •31. Үзіліссіздік және бірқалыпты үзіліссіздік.
- •33.Туынды және оның интерпретациясы. Жанама.
- •34) Дифференциялдау және арифметикалық амалдар.
- •35. Күрделі функцияның туындысы. Кері функцияның туындысы.
- •36. Біржақты туындылар. Туындының бар болуы.
- •37. Функцияның экстремум мәндері. Олардың қажетті шарты.
- •38. Ролль теоремасы.
- •39. Туындының аралық мәні туралы теорема.
- •42. Лопиталь ережесі. Анықталмағандықтар.
- •43) Тейлор теоремасы
- •44. Тейлор теоремасын локальді экстремумға қолдану. (негізі: Тейлордың локальдық формуласын экстремумға қолдану)
- •46.Дифференциалданатын функцияның үзіліссіздігі. Дифференциалданбайтын фукцияның үзіліссіздігі.
- •48. Монотонды функцияның үзіліссіз болуы туралы критерий.
- •49. Үзіліссіз және бірқалыпты үзіліссіз емес функцияның мысалы
- •50. Үзіліссіз функциялар үшін кері функцияның бар болуы туралы теорема.
- •Реттік қатынас. Көбейту және қосу амалдарымен байланысы. Реттелген өрістер.
- •Санның абсолюттік шамасы. Үшбұрыш теңсіздігі. Оның салдары.
- •Жиынның жоғарғы жағы. Жоғарыдан шенелген жиын. Супремум.
38. Ролль теоремасы.
Теорема.
функциясы
сегментінде үзіліссіз болып,
интервалында дифференциалдансын. Егер
сегменттің шеткі нүктелеріндегі
функцияның мәндері өзара тең болса,
яғни
 теңдігі орындалса, онда
теңдігі орындалса, онда
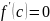 шартын қанағаттандыратын кемінде бір
шартын қанағаттандыратын кемінде бір
 саны табылады.
саны табылады.
Дәлелдеуі.
Егер
тұрақты болса, яғни
 болса, онда
болса, онда
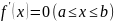 болады, демек, бізге қажетті
болады, демек, бізге қажетті
 ретінде
интервалының әрбір нүктесін алуға
болады.
ретінде
интервалының әрбір нүктесін алуға
болады.
Енді
тұрақты болмасын. Онда
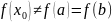 шартын қанағаттандыратын
шартын қанағаттандыратын
 саны табылады. Анықтық үшін
саны табылады. Анықтық үшін
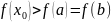 болсын.
үзіліссіз болғандықтан, Вейерштрасс
теоремасы бойынша барлық
үшін
болсын.
үзіліссіз болғандықтан, Вейерштрасс
теоремасы бойынша барлық
үшін
 теңсіздігі орындалатын
теңсіздігі орындалатын
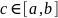 саны табылады. Расында,
саны
сегментінің ішкі нүктесі болады, яғни
интервалында жатады, өйткені
үшін
саны табылады. Расында,
саны
сегментінің ішкі нүктесі болады, яғни
интервалында жатады, өйткені
үшін
 ,
демек,
саны
мен
-дан
өзге.
,
демек,
саны
мен
-дан
өзге.
Енді
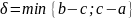 болса, онда 1)
болса, онда 1)
 ,
яғни
-ның
-маңайында
функциясы анықталған, 2) әрбір
,
яғни
-ның
-маңайында
функциясы анықталған, 2) әрбір
 үшін
үшін
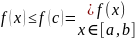 демек, анықтама бойынша
максимум нүктесі, ал
демек, анықтама бойынша
максимум нүктесі, ал
 бар болғандықтан, Ферма теоремасы
бойынша мақсатымыз болатын
теңдігіне келеміз. Теорема дәлелденді.
бар болғандықтан, Ферма теоремасы
бойынша мақсатымыз болатын
теңдігіне келеміз. Теорема дәлелденді.
Ролль теоремасы
[а,b] аралығында f(х) анықталған сондай-ақ:
[а,b] аралығында f(х) – үзіліссіз;
[а,b] аралығында f(х)дифференциалдасын;
f(a)=f(b)
Онда f ’ (c) =0 болатындай с € (a,b) табылады.
Дәлелдеу: f(x) функциясы [а,b] аралығында үзіліссіз болсын. Вейер – Штрасстың теоремасы бойынша бұл кесінді де максималды, минималды (M,m) арқылы болады.(Вейер-Штрасс теоремасы: Егер f(х) функциясы [а,b] кесіндісінде анықталған және үзіліссіз болса, онда бұл аралықта өзінің дәл төменгі шекарасына жетеді. Ең үлкен және ең кіші мәндері бар болады).
2 жағдай болуы мүмкін :
M=m
m<M
1-жағдай бойынша f(х) = const; m=M, онда f ‘ (х)=0
2-жағдай бойынша f(a)= f(b) болсын. m,Mмәндерінің біреуі [а,b] ұштарында емес, яғни f(с)= m және f(с)=M. Бұл жағдайда f ‘(с)=1 , f ‘(с)=0 табылады.
39. Туындының аралық мәні туралы теорема.
Теорема. 1) функциясы аралығыныда дифференциалданса;
2)
 болсын;
болсын;
3)
 саны
саны
 мен
мен
 -ның арасында жатсын
-ның арасында жатсын
Сонда,
 болатындай
болатындай
 саны табылады.
саны табылады.
Дәлелдеуі.
 болсын
болсын
 –
үзіліссіз, дифференциалданады.
–
үзіліссіз, дифференциалданады.



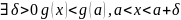
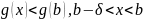
-экстримум нүктесі болса, онда
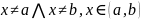 Локальды
экстремум нүктесі
Локальды
экстремум нүктесі


40-41-43. Аралық мән туралы жалпыланған теорема.
Tеорема:
Егер
f
функциясы
 интервалында
үзіліссіз болып
интервалында
үзіліссіз болып
 болсын
болсын
 арасында жатсын сонда
арасында жатсын сонда
 )=
болатындай с
)=
болатындай с
Дәлелдеуі:
 болсын S={
болсын S={ }
S шенелген с=supS
}
S шенелген с=supS
S кері
жоримыз
кері
жоримыз

 c-да
f
үзіліссіз
c-да
f
үзіліссіз
 с-
<x<c
үшін
с-
<x<c
үшін
 болатындай
болатындай
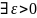 олай
болса
с-
S
жиынының
жоғарғы жағы с-ның таңдауына қайшы.
олай
болса
с-
S
жиынының
жоғарғы жағы с-ның таңдауына қайшы.
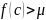 с<b
с<b

 c
жоғарғы жақ емес с=supS
c
жоғарғы жақ емес с=supS

Үзіліссіз функцияның аралық мәні туралы
1-теорема (Больцано-Коши). Егер кесіндіде үзіліссіз функцияның кесінді ұштарындағы мәндерінің таңбалары әртүрлі болса, онда осы кесіндіден функция мәні нөлге айналатын нүкте табылады.
Бұл теореманы логикалық символика арқылы былай жазар едік:

Дәлелдеу.
кесіндісін екіге бөлейік. Егер бөлген
нүктеде функция нөлге тең болмаса, онда
алынған екі кесіндінің біреуінің
ұштарында функция әртүрлі таңбалы мән
қабылдайды. Оны тағы екіге бөліп, осы
процесті жалғастыра береміз. Сонда
белгілі бір қадамнан соң
 болатын
болатын
 нүктесіне түссек теорема дәлелденген
болады. Немесе нөлге ұмтылатын
нүктесіне түссек теорема дәлелденген
болады. Немесе нөлге ұмтылатын
 енгізілген кесінділер тізбегін аламыз.
Бұл жағдайда Коши-Кантор енгізілген
принципі бойынша осы алынған кесінділердің
бәріне ортақ жалғыз
нүктесі табылады. Құрғанымыз бойынша
енгізілген кесінділер тізбегін аламыз.
Бұл жағдайда Коши-Кантор енгізілген
принципі бойынша осы алынған кесінділердің
бәріне ортақ жалғыз
нүктесі табылады. Құрғанымыз бойынша
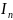 кесіндісінің ұштарынан түзілген
кесіндісінің ұштарынан түзілген
 болатын
болатын
 және
және
 болатын
болатын
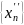 екі тізбегін алдық әрі бұл тізбектер
шектері
екі тізбегін алдық әрі бұл тізбектер
шектері
 Тізбек шегінің қасиеті мен үзіліссіздік
анықтамасынан
Тізбек шегінің қасиеті мен үзіліссіздік
анықтамасынан
 және
және
 Сонымен
Сонымен
 Теорема дәлелденді.
Теорема дәлелденді.
2-теорема
(Коши).
Егер
функциясы
кесіндісінде үзіліссіз және
 болса, онда
болса, онда
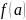 және
және
 сандарының арасындағы кез келген С
саны үшін
сандарының арасындағы кез келген С
саны үшін
 болатын ең болмағанда бір
болатын ең болмағанда бір
 нүктесі табылады.
нүктесі табылады.
Бұны да логикалық символика арқылы былай жазуға болады:
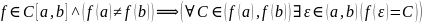
Дәлелдеуі.
 болғандықтан
болғандықтан
 Теорема
дәлелденді.
Теорема
дәлелденді.
