35. Күрделі функцияның туындысы. Кері функцияның туындысы.
Күрделі функцияның туындысы.
функциясының
сегментінде анықталып, оның мәндерінің
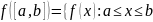жиыны
функциясы анықталған
сегментінің жиыншасы болсын. Онда
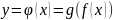күрделі функциясы
сегментінде анықталған болады.
Теорема.
Егер
функциясының
нүктесінде туындысы бар болып,
функциясының
нүктесінде туындысы бар болса, онда
күрделі функциясының
нүктесінде туындысы бар болып,
(1)
болады.
Дәлелдеуі.
Алдымен
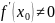болсын. Онда 0-дің белгілі бір ойылған
маңайындағы барлық
сандары үшін функцияның мәндері шектің
мәнін сақтайтыны туралы теорема бойынша
теңсіздігі орындалады. Сондықтан,
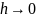болғанда шегін табу керек болатын
өрнегін
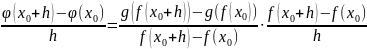түрінде бейнелеуге болады. Бұдан (1)
теңдігі шығады, өйткені
функциясы
нүктесінде, ал
функциясы
нүктесінде үзіліссіз болғандықтан,
үшін
теңдігі орындалады.
Енді
болсын.
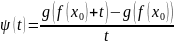үшін туындының анықтамасы бойынша
болады,
демек,
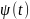функциясы 0 нүктесінде локальді шенелген
болады, яғни
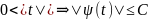шарты орындалатын
және С оң сандары табылады.
теңсіздігін қанағаттандыратын
саны берілсін. Онда
және
болғандықтан
(2)
және
(3)
шарттары
орындалатын
және
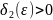сандары табылады. Егер
саны үшін
(4)
шарты
орындалатынын дәлелдесек, онда біздің
мақсатымыз болатын
теңдігі де дәлелденген болады.
Сонымен
(4)-ні
дәлелдейік.
болсын. Алдымен
үшін
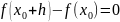болсын. Онда
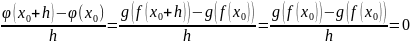
болады,
яғни сондай
үшін (4)
орындалады.
Ал
болғанда
үшін (2)
бойынша
(5)
теңсіздігі
орындалады.
Сонымен,
(3)
және (5)
бойынша
болады, яғни (4)
бұл жағдайда да орындалады.
Теорема толық дәлелденді.
Кері функцияның туындысы.
функциясы
сегментінде өспелі және үзіліссіз
болсын. Онда оның
сегментінде анықталған және үзіліссіз
болатын
кері функциясы бар болады.
Кемімелі функция туралы да дәл осыны айтуға болады.
Теорема.
Егер
функциясы
сегментінде өспелі және үзіліссіз
болып,
нүктесінде
нольге тең емес туындысы бар болса,
онда
кері функциясының да
нүктесінде туындысы бар болып,
теңдігі орындалады.
Дәлелдеуі.
болсын. Кері функцияның анықтамасы
бойынша әрбір
саны үшін
(1)
теңдіктерін қанағаттандыратын
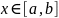саны бар және жалңыз болады.
үзіліссіз болғандықтан
(2)
шарты орындалады. Сондықтан (1)
және
(2)
бойынша
Теорема толық дәлелденді.
36. Біржақты туындылар. Туындының бар болуы.
,
,
,
Егер
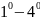-дегі
шектерді оң жақты және сол жақты шектреге
өзгертсек, онда
функциясының
нүктесіндегі сәйкес оң және сол жақты
туындыларының анықтамаларына келеміз.
Оң жақты туындыны
,
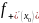ал сол жақ туындыны
символдарымен белгілейді. Сонымен,
сегментінде анықталған функциясының нүктесінде тек қана оң жақты, ал нүктесінде тек қана сол жақты туындылары туралы айтуға болады. Әрине, функциясының нүктесінде жай туындысы бар болуы үшін, оның сол нүктеде оң және сол жақты туындылары бар болып, олар өзара тең болуы қажетті және жеткілікті.
Егер -дегі өрнектердің жай, оң немесе сол жақты ақырсыз шегі бар болса, онда функциясының нүктесінде сәйкес жай, оң немесе сол жақты ақырсыз туындысы бар дейді.
Шек ұғымы арқылы функцияның екі қасиетін анықталады – ол үзіліссіз болуы мен туындысы бар болуы.
функциясы І аралығында анықталып, болсын.
Теорема. Егер функциясының нүктесінде жай, оң немесе сол жақты ақырлы туындысы бар болса, онда сол нүктеде сәйкес жай, оң немесе сол жақты үзіліссіз болады.
Дәлелдеуі.
функциясының
нүктесінде жай туындысы бар болсын.
Әрбір
үшін
болады, демек, көбейтіндінің шегі туралы
теорема бойынша
,
яғни
функциясының
нүктесінде үзіліссіз.
Мұның
ешқандай теоремаға сүйенбейтін тіке
дәлелдеуін де беруге болады. Расында
да,
саны берілсін. Онда шектің анықтамасы
бойынша
теңсіздігін қанағаттандыратын барлық
сандары
үшін
(1)
теңсіздігі орындалатын
оң саны табылады. Аталған
сандары үшін(1)-тен
келесі
теңсіздік шығады. Сондықтан,
болса, онда
шарты орындалады, ал бұл
функциясының
нүктесіндегі үзіліссіздігінің дәл өзі
болады.
Біржақты туындылар жағдайында да теорема дәл осылай дәлелденеді.
Салдар. Егер нүктесін функциясының үзіліссіз нүктесі болса, онда сол нүктеде -тің ақырлы туындысы болмайды.