33.Туынды және оның интерпретациясы. Жанама.

функциясының графигін, яғни жазықтықта жатқан 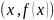түріндегі нүктелер жиынын қарастырайық (оны 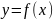қисығы не жай қисық деп те атайды).

Біздің мақсатымыз белгілі бір ( нүктесінде қисыққа «тығыз орналасқан» түзуді сызу. Қисықта жатқан басқа нүктесін алып, сол екі нүктеден түзу өткізейік. Оның теңдеуі:

болады. Әрбір ( нүктесінен өтетін және -тер осіне параллель емес түзудің теңдеуі түрінде жазылады, демек, нақты санына тәуелді болады.

Әрине, белгілі бір мағынада екі түзудің жақындығын оларды анықтайтын сандарының жақындығы арқылы түсінуге болады.

Сондықтан, -ді -ге ақырсыз жақын алған сайын, белгілі бір санына ақырсыз жақындаса, онда теңдеуі болатын түзуді бізге керекті «қисыққа тығыз орналасқан» түзу ретінде алуға болады.

Сонымен, егер: нүктесінде нақты мәнді шегі бар болса, онда түзуі қисығының нүктесіндегі жанамасы деп аталады.

Материялық нүкте түзу бойымен белгілі бір бағытта қозғалып келе жатсын. Оның түзу бойындағы белгілі бір нүктеден мезгіліндегі ара қашықтығы 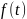болсын. Әуелі болсын, яғни нүкте бірқалыпты қозғалсын. Онда кез келген мен мезгілдері арасында нүкте 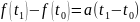жолын жүреді, ал қатынасы сол қозғалыстың жылдамдығы деп аталады да, тұрақты болып, санына тең болады.

Егер нүктенің қозғалысы бірқалыпты болмаса, онда қатынасы тұрақты болмай мен мезгілдеріне тәуелді болады. Ол мен мезгілдері арасындағы материялық нүктенің қозғалысының орташа жылдамдығы деп аталады. Орташа жылдамдықтың мағынасы мынада: егер нүкте сол арада бірқалыпты қозғалса, онда мезгілінде жолын жүру үшін оның жылдамдығы орташа жылдамдыққа тең болуы тиіс.

Егер -ді -ге ақырсыз жақындатқанда, оған сәйкес орташа жылдамдығы белгілі бір нақты санға ақырсыз жақындаса, онда сол санды мезгіліндегі нүктенің жылдамдығы түрінде алған жөн.

Егер нақты мәнді шегі бар болса, онда оны тәртібі арқылы бейнеленген қозғалыстың нүктесіндегі жылдамдығы деп атайды.

Бұл амалдың өзін функцияны дифференциалдау, ал оның нәтижесін, яңни шектің мәнін функцияның туындысы дейді.

Сөйтіп, функциясы І аралығында анықталсын. Егер үшін нақты мәндә шегі бар болса, онда функциясын нүктесінде дифференциалданады, ал шектің мәнін функциясын нүктесіндегі туындысы дейді де, символымен белгілейді.

Туындының анықтамасын шекті белгілейтін символдарды пайдаланып былай жазуға болады:

,

,

,

,

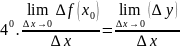сандары функцияның аргументінің немесе тәуелсіз айнымалының өсімшесі деп аталады.

34) Дифференциялдау және арифметикалық амалдар.

y=f(x)-сы нүктесінде дифференциалдансын, яғни бұл нүктеде өсімшесі 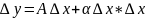формуласы түрінде жазылады. қосылғышы -ге ұмтылғанда -пен бірдей ретті ақырсыз аз болады. . Сонымен 1-қосылғыш ) y=f(x)-сының бас бөлігі д.а. , -бас бөлігі.

Анық: y=f(x)-ның х₀ нүктесіндегі дифференциалы деп -ке сызықты қатысты осы нүктедегі функцияның өсімшесінің бас бөлігі аталады және оны былай белгілейді: .

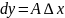Th-1: y=f(x)-сы нүктесінде дифференциалдануы үшін берілген нүктеде функцияның ақырлы туындысы болуы қажетті және жеткілікті. Осыныескерсек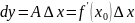 . Айталық f(x)=xболсын, онда формула бойынша

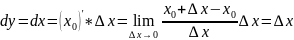
- функцияның дифференциалдық аргументіне қатынасы.