Задача 5

Для распределительного вала, который принимает мощность Р₁ = 100 кВт и распределяет её по звеньям механизма следующим образом: Р₂ = 50 кВт, Р₃ = 30 кВт, Р₄ = 20 кВт при частоте вращения n = 1000об/мин (рис.8): построить эпюру крутящих моментов, определить из условия прочности диаметры его ступеней (полученные значения диаметров округлить в большую сторону до целого чётного, или кратного пяти числа) и проверить вал на жесткость, если допускаемое напряжение Н/мм², допускаемый удельный угол закручивания град/м. Величину модуля упругости второго рода принять для стали Н/мм².

ПРИМЕЧАНИЕ: номер схемы- 2 цифра шифра

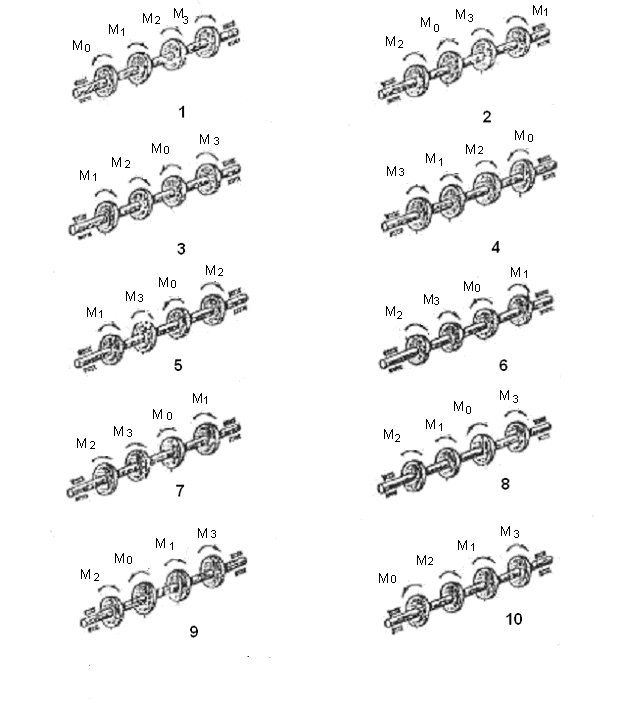
Рис.8 . Расчётные схемы распределительного вала

ПРИМЕР 5

Построить эпюру крутящих моментов для распределительного вала, который принимает мощность Р₁ = 100 кВт и распределяет её по звеньям механизма следующим образом:

Р₂ = 50 кВт, Р₃ = 30 кВт, Р₄ = 20 кВт при частоте вращения n = 1000об/мин (рис.9).

Эпюра крутящих моментов для распределительного вала строится по следующему правилу:

• Составляется расчётная схема вала, которая представляет собой вал с действующими на него скручивающими моментами. Скручивающие моменты определяются по формуле:

, где Р (Вт) – мощность на звене; n (об/мин) – частота вращения вала.

Скручивающие моменты действуют в тех поперечных сечениях, в которых установлены принимающее и отдающие звенья. Направления скручивающих моментов выбираются произвольно с обязательным соблюдением условия, чтобы направления скручивющих моментов на отдающих звеньях было противоположно направлению скручивающего момента на принимающем (1) звене (рисунок 38).

Нм Нм

Нм Нм

• Параллельно оси вала проводится нулевая линия эпюры и переносятся на неё сечения, в которых действуют скручивающие моменты. В результате этого вся длина вала разделяется на характерные участки, на протяжении каждого из которых величина крутящего момента постоянна (рисунок 38).

• Начиная с левого конца вала методом «прямых скачков» строим эпюру крутящих моментов. «Прямые скачки» - это скачки в направлении скручивающих моментов на их величину. При следовании справа налево применяется метод «обратных скачков», т. е. скачков на величину скручивающих моментов в противоположную их направлениям сторону.

Эпюра крутящих моментов на каждом характерном участке представляет собой прямую линию, параллельную нулевой линии (рис.9).

Построенная эпюра крутящих моментов показывает, что заданный распределительный вал имеет нерациональную расчётную схему, т. к. нагрузка на него неравномерна. Это приведёт в конечном итоге к многоступенчатой конструкции вала с большой разницей между диаметрами ступеней и большому количеству отходов при его изготовлении. Заданную расчётную схему необходимо преобразовать в рациональную, поменяв местами скручивающие моменты. Принимающее (1) звено следует располагать между отдающими звеньями с максимальным (2) и минимальным (4) скручивающими моментами

(рис.9 рациональная расчётная схема).

Эпюра крутящих моментов для рациональной расчётной схемы строится аналогично ранее построенной эпюре.

Рациональная расчётная схема распределительного вала позволяет:

1. Максимально выровнять нагрузку на вал по его длине, уменьшив её наибольшее значение и увеличив наименьшее.

2. Уменьшить материалоёмкость вала.

3. Уменьшить количество отходов при его изготовлении, увеличив тем самым коэффициент использования материала.

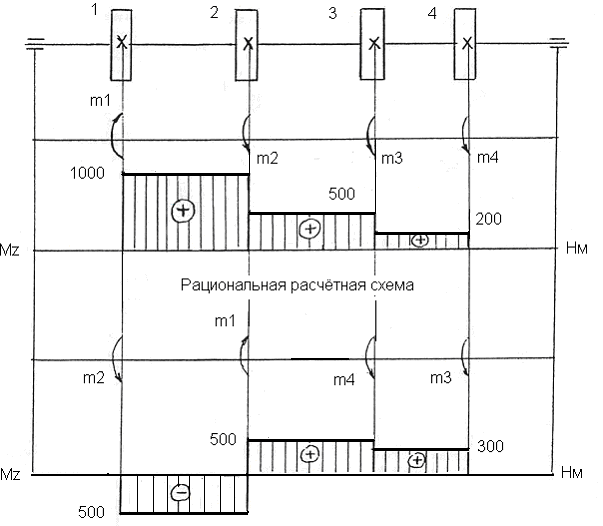
Рис.9. Расчётные схемы распределительного вала и эпюры крутящих моментов

Определить из условия прочности диаметры его ступеней, если допускаемое напряжение Н/мм². Полученные значения диаметров округлить в большую сторону до целого чётного, или кратного пяти числа.

Производим проектный расчёт на прочность при кручении. Формула расчёта:

, где

d, (мм) – диаметр ступени распределительного вала;

М_z (Нмм) – крутящий момент в поперечном сечении распределительного вала;

(Н/мм²) – допускаемое напряжение для материала распределительного вала.

Определим диаметры ступеней распределительного вала, используя построенную ранее рациональную расчётную схему и эпюру крутящего момента (рисунок 9).

Диаметр ступени вала, на которой действует крутящий момент 300 Нм: мм. Принимаем окончательно d = 44 мм (ближайшее большее чётное число).

Диаметр ступеней вала, на которых действуют крутящие моменты 500 Нм и -500 Нм:

мм. Принимаем окончательно d = 50 мм (число, кратное пяти).

Диаметры ступеней вала, на которых не действует крутящий момент, принимаем равными наименьшему расчётному значению, т. е. d = 44 мм.

ЗАДАЧА 6

По данным задачи 2 для двухопорной балки построить эпоры поперечных сил Qу и изгибающих моментов М_х. Подобрать сечение стального двутавра, приняв

[σ] = 160 МПа.

ПРИМЕР 5

Для двухопорной балки построить эпюры поперечных сил Q и изгибающих моментов М. Подобрать сечение стального двутавра, приняв [σ] = 160 МПа.

Дано: F₁=24 kH; F₂=36 кН; m₁=18 кНм;

m₂=24 кНм; =2.0 м; м; м.

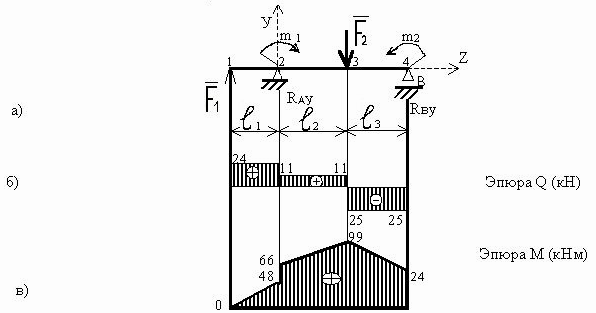
Рисунок - 10

Решение

1 Составляем уравнение равновесия параллельной системы сил, из которых определяем опорные реакции балки:

(5)

₍₆₎

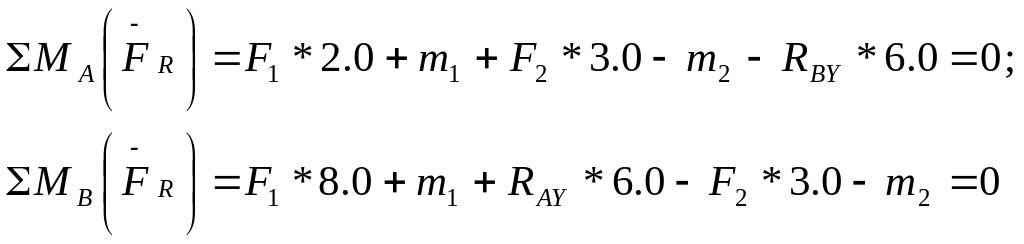
Из уравнения (6) находим R_AУ:

Из уравнения (5) находим В:

Проверяем правильность определения опорных реакций, составляя сумму проекций всех сил на ось У:

то есть реакции определены верно.

2 Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначим цифрами 1, 2, 3, 4 (рисунок 10 а)

Q₁=Q₂^лев=F₁=24 кН;

Q₂^прав=Q₃^лев=F₁+R_АУ=24-13=11 кН;

Q₃^2прав=Q₄=F₁+R_АУ-F₂= -R_ВУ= -25 кН.

По найденным значениям строим эпюру, поперечных сил Q (рисунок 10 б).

3 Аналогично определяем значения изгибающего момента М в характерных сечениях балки:

М₁=0;

М₂^лев=F₁*2.0=48 кНм

М₂^прав=М₂^лев+m₁=48+18=66 кНм;

М₃=F₁*5.0+m₁+R_АУ*3,0=120+18-39=99 кНм;

М₄=m₂=24 кНм.

По найденным значениям строим эпюру изгибающих моментов М (рисунок 10 в).

4 По эпюре изгибающих моментов определяем положение опасного сечения балки (сечение, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае – это сечение 3, где М₃=М_maх=99 кНм. Из условия прочности балки на изгиб вычисляем необходимый осевой момент сопротивления:

.

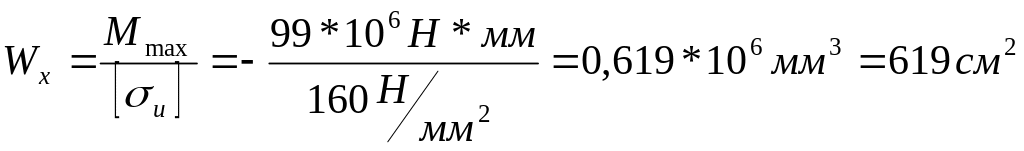В соответствии с ГОСТ 8239-89 принимаем сечение из стального двутавра № 33 с Wх=597 см³. Имеем перенапряжение:

< 5%

что находится в разрешенных пределах (менее 5%).

Ответ: сечение балки двутавр № 33.

ЗАДАЧА 7

О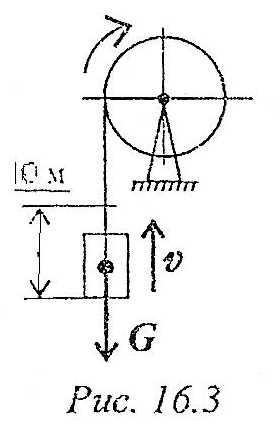 пределить потребную мощность мотора лебёдки для подъёма груза весом 3кН на высоту 10м за 2,5 с (рис. 11). КПД механизма лебёдки 0,75

Вариант	1	2	3	4	5	6	7	8	9	10
Вес груза, кН	4	5	6	7	8	9	10	11	12	13
Высота, м	11	12	13	14	15	16	17	18	19	20
Время подъёма, с	3,5	4,5	5,5	6,5	7,5	8,5	9,5	10,5	11,5	12,5
КПД	0,76	0,77	0,78	0,79	0,8	0,81	0,82	0,83	0,84	0,85

Рисунок - 11

Пример расчёта:

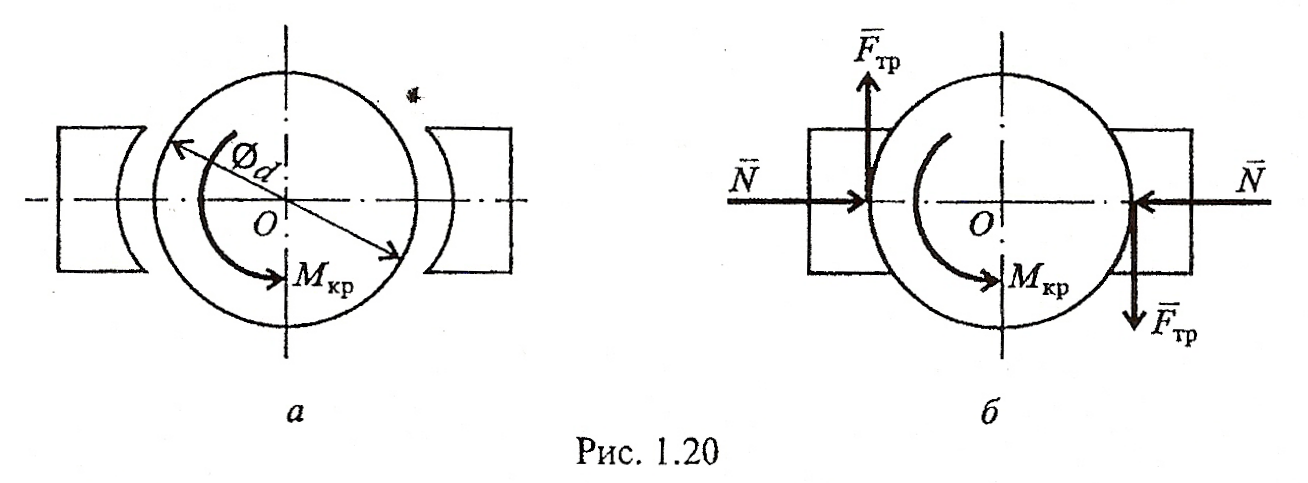
ЗАДАЧА 8 На стал ной вал ( рис.12)действует крутящий момент500кНм

Определить, с какой силой нужно сжать тормозные колодки, обтянутые кожей, чтобы остановить вал.

Вариант	1	2	3	4	5	6	7	8	9	10
Крутящий момент, кН*м	520	530	540	550	560	570	580	590	600	610

Рисунок - 12

Пример решения