Билет №24.

Задача №1. Найти острые углы прямоугольного треугольника, если медиана, проведённая к его гипотенузе, делит прямой угол в отношении 1:2.

Д ано: , CO – медиана,

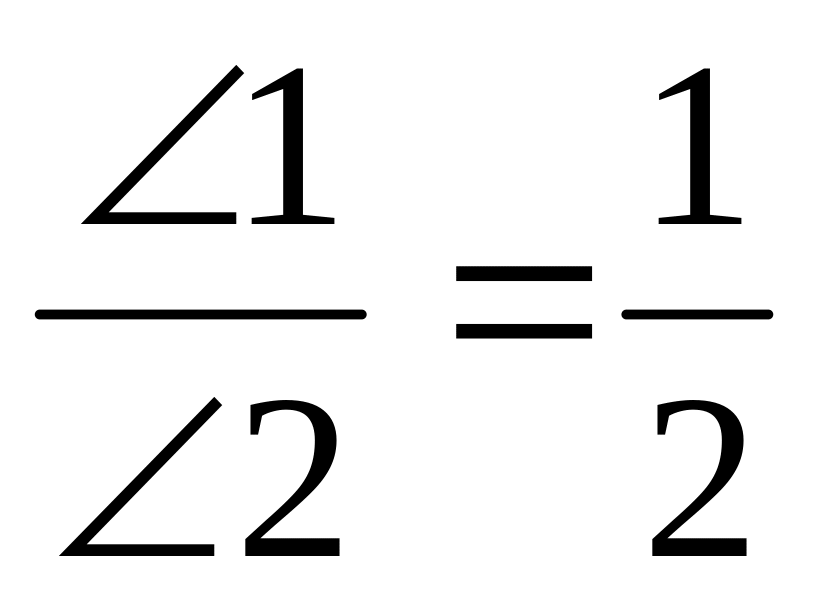
Решение.

О – центр описанной окружности, т.к. О – середина гипотенузы.

1)

- равнобедренный,

2) Аналогично

Ответ: , .

З адача №2. Доказать, что биссектриса прямого угла прямоугольного треугольника делит пополам угол между медианой и высотой, проведёнными к гипотенузе.

Дано: - прямоугольный, CH – высота, CK – биссектриса, CC₁ – медиана.

Доказательство.

1) Т.к. - прямоугольный, то центр описанной окружности лежит на середине гипотенузы, т.е. в точке (т.к. – медиана),

2) , но , т.к. - равнобедренный

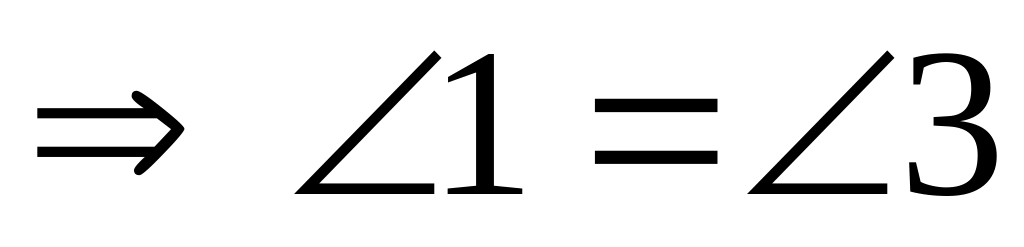
3) , т.к. CK – биссектриса, тогда , ч.т.д.