Билет №20.

Задача №1. Найдите площадь треугольника с вершинами А(1; 4), В(-3; -1), С(2; -2).

Дано: А(1; 4), В(-3; -1), С(2; -2).

Решение.

1)

2) В - большая сторона. По теореме косинусов:

3) кв.ед.

Ответ: кв.ед.

Задача №2. Даны координаты вершин треугольника АВС: А(4; 6), В(-4; 0), С(-1; -4). Написать уравнение прямой, содержащей медиану СМ.

Дано: , А(4; 6), В(-4; 0), С(-1; -4), СМ – медиана.

Решение.

Т.к. М – середина ВА, то

.

Уравнение прямой СМ имеет вид , т.к. прямая проходит через точки С и М, то координаты этих точек удовлетворяют уравнению прямой.

Уравнение медианы СМ имеет вид

Ответ: .

Билет №21.

Задача №1. Найдите площадь квадрата, вписанного в ромб со стороной 6 см и углом 30⁰ (сторона квадрата параллельна диагонали ромба).

Д ано: ABCD – ромб, , , MNKL – вписанный квадрат.

Решение.

Пусть - половина стороны квадрата.

Дополнительные построения: диагональ AC и AB.

1) - прямоугольный,

2)

(по двум углам)

Пусть

Сторона квадрата ,

Ответ:

Задача №2. Найдите длину отрезка, параллельного основаниям трапеции (их длины a и b) и делящего трапецию на два подобных четырехугольника.

Дано: ABCD – трапеция, , ,

Решение.

Т.к. подобными четырехугольниками называются четырехугольники, у которых все углы соответственно равны и стороны пропорциональны, то из

Ответ: .

Билет №22.

Задача №1. Найдите площадь фигуры, ограниченной дугами трёх попарно касающихся окружностей радиусов 1, 1 и -1.

Д ано: Окр(О₁;1), Окр(О₂;1), Окр(О₃; ), А, В, С – точки касания.

Решение.

1) , причем

2) Рассмотрим

,

Тогда кв.ед.

3) В , а , т.к. - равнобедренный.

А)

Б)

4) (кв.ед.)

Ответ: (кв.ед.)

Задача №2. Круги радиусов 1, 6 и 14 касаются друг друга. Найдите радиус окружности, вписанной в треугольник с вершинами в центрах данных кругов.

Дано: Окр(О₁;1), Окр(О₂;6), Окр(О₃;14), А, В, С – точки касания.

Решение.

В , , .

, где

По формуле Герона:

, тогда

Ответ: .

Билет №23.

Задача №1. Докажите, что биссектриса АА₁ треугольника АВС вычисляется по формуле: АА₁= .

Д ано: , - биссектриса.

Доказательство.

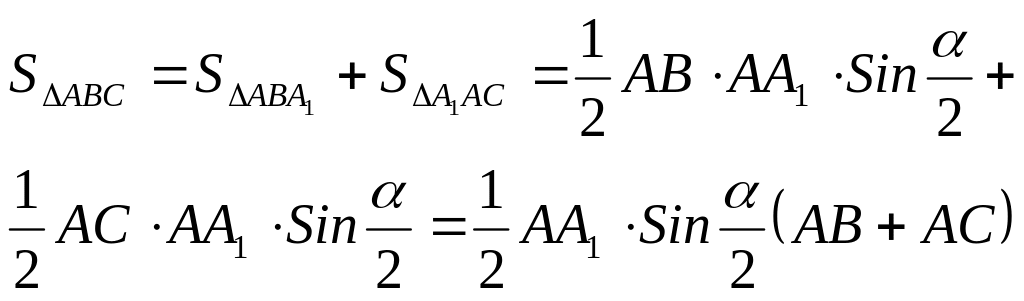
, ч.т.д.

З адача №2. Докажите, что медиана треугольника со сторонами a, b, c, проведённая к стороне а, вычисляется по формуле: .

Дано: , а, b, c –стороны, - медиана.

Решение.

I способ.

Рассмотрим векторы , , , A₁ –

середина ВС, значит .

Заметим, что

II способ.

1) Рассмотрим : пусть

2) Рассмотрим :

3) :

, откуда , ч.т.д.