§7 Системы лду 1 порядка с постоянными коэффициентами; операционный метод решения задачи Коши.
Пусть
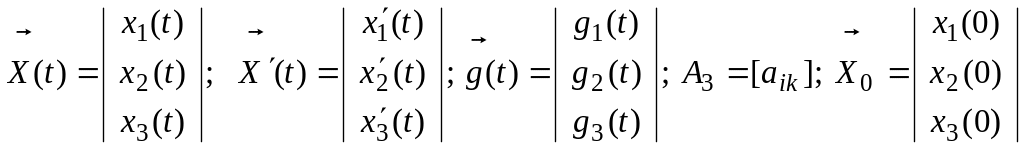
Тогда уравнение
 определяет систему ЛДУ, а
определяет систему ЛДУ, а
 (1)
(1)
- задачу Коши с начальными условиями
для этой системы.
Например, для
 система (1) имеет явный вид:
система (1) имеет явный вид:
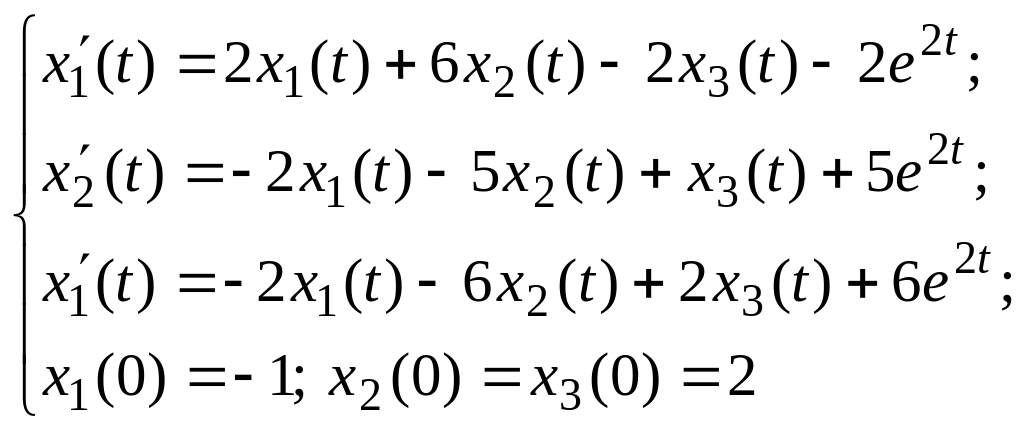
Предположим, что функции
 являются
оригиналами. Выполним для уравнения
(1) преобразование Лапласа:
являются
оригиналами. Выполним для уравнения
(1) преобразование Лапласа:

Таким образом, преобразование Лапласа
отображает задачу Коши для системы ЛДУ
во множестве оригиналов в систему
линейных алгебраических уравнений
 во
множестве изображений, причем матрица
СЛАУ равна
во
множестве изображений, причем матрица
СЛАУ равна
 ,
а вектор правых частей равен
,
а вектор правых частей равен
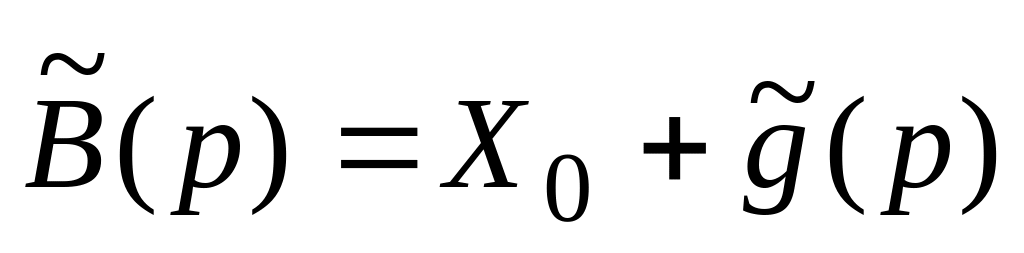 .
.
Соответствующая СЛАУ для рассматриваемого
примера имеет вид:

Решение СЛАУ будем искать по теореме
Крамера





Обратное преобразование Лапласа
восстанавливает оригинал - вектор-решение
задачи Коши



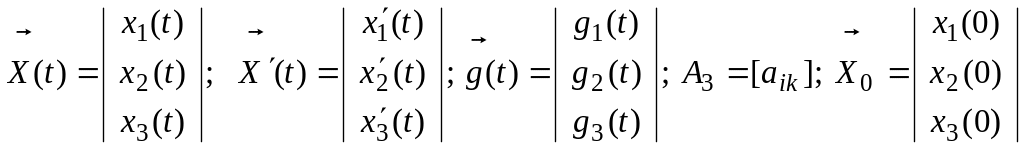
 система (1) имеет явный вид:
система (1) имеет явный вид:



