15. Геометрический и Механический смысл производной.

Производная. Приращение аргумента. Приращение функции.

Дифференцируемая функция. Геометрический смысл производной.

Угловой коэффициент касательной. Уравнение касательной.

Механический смысл производной. Средняя и мгновенная скорость.

Ускорение.

 

Производная. Рассмотрим некоторую функцию  y = f ( x ) в двух точках  x₀  и  x₀ +  :  f ( x₀ ) и  f ( x₀ +   ). Здесь через   обозначено некоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции:  f ( x₀ +   )  f ( x₀ ) называется приращением функции. Производной функции  y = f ( x ) в точке  x₀  называется предел:

Если этот предел существует, то функция   f ( x )  называется дифференцируемой в точке  x₀ . Производная функции   f ( x ) обозначается так:

Геометрический смысл производной.  Рассмотрим график функции  y = f ( x ): 

Из рис.1  видно, что для любых двух точек A и B графика функции:  

где    - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то   неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x₀ ,  f ( x₀  ) ). В общем случае уравнение прямой с угловым коэффициентом f ’( x₀ )  имеет вид: 

y = f ’( x₀ ) · x + b .

Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:

f ( x₀ ) = f ’( x₀ ) · x₀ + b ,

отсюда,  b =  f ( x₀ ) – f ’( x₀ ) · x₀ , и подставляя это выражение вместо  b, мы получим  уравнение касательной:

y =  f ( x₀ ) +  f ’( x₀ ) · ( x – x₀  ) .

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ +    точка перемещается на расстояние:  x ( t₀ +  )  x ( t₀ ) =  , а её средняя скорость равна:  v_a =    . При      0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

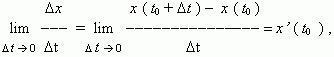
отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной. Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

16. Правила дифференцирования. Производные сложной, обратной и неявной функций.

1)Правила Дифференцирования.

Если функции f и g дифференцируемы в точке x0, то в этой же точке дифференцируемы сумма, произведение и частное (если g (x0) =0) этих функций, причем

1. (f+g) =f +g

2. (f g) =f g+f g

3. (fg) =g2f g−f g

Постоянный множитель C можно выносить из-под знака производной: (Cf)' = Cf'. В частности, С'=0

• Если f дифференцируема,  то fn где n N также дифференцируема, причем (fn) =nfn−1f

• Если функция y = f (x) непрерывна и строго возрастает в окрестности точки x0 причем f (x0) =0,  то функция x = 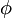  (y),обратная к функции y = f (x), дифференцируема в точке y0 = f (x0), причем  (x0)=1f (x0).

• Если функции y = f (x) и z = g (y) дифференцируемы в точках x0 и y0 = f (x0) соответственно,  то сложная функция z = g ( f (x)) дифференцируема в точке x ₀, причем z (x0)=g (y0) f (x0).

• Дифференциал функции y = f (x) имеет один и тот же вид dy=f (x)dx как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного.

• Если f (x) – четная функция, то f (x) – нечетная; если f (x ) – нечетная функция, то f (x) – четная.

• Пусть в окрестности точки t ₀ определены функции x (t) и y (t), причем x (t) непрерывна и строго монотонна.  Пусть в этой окрестности существуют производные x (t0) =0 и y (t0)  Тогда сложная функция y = y ( t ( x )), где t ( x ) – функция, обратная x (t), дифференцируема по x , причем dxdy=x (t)y (t).

### 2)Производные сложной функции.

Функции сложного вида не совсем корректно называть термином «сложная функция». К примеру, 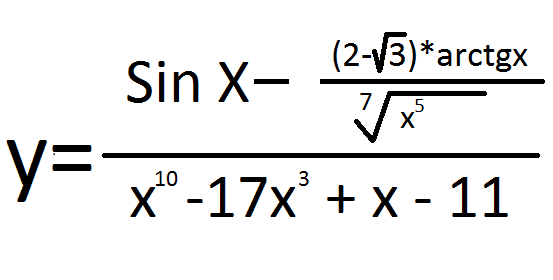  смотрится очень внушительно, но сложной эта функция не является, в отличие от  .

В этой статье мы разберемся с понятием сложной функции, научимся выявлять ее в составе элементарных функций, дадим формулу нахождения ее производной и подробно рассмотрим решение характерных примеров.

При решении примеров будем постоянно использовать таблицу производных и правила дифференцирования, так что держите их перед глазами.

Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать какf(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а   - целая рациональная функция (смотритеклассификацию элементарных функций), тогда  .

В свою очередь, g(x) также может быть сложной функцией. Например, 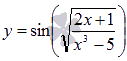 . Условно такое выражение можно обозначить как  . Здесь f – функция синуса,   - функция извлечения квадратного корня,   - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом  .

Часто можно слышать, что сложную функцию называют композицией функций.

Формула нахождения производной сложной функции. (f(g(x)))’ = f’(g(x))*g’(x)

### 3)Производные обратной функции.

Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть,   - это производная функции f(x) по x.

Теперь сформулируем правило нахождения производной обратной функции.

Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах   и   соответственно. Если в точке   существует конечная отличная от нуля производная функции f(x), то в точке   существует конечная производная обратной функции g(y), причем  . В другой записи  .

Можно это правило переформулировать для любого x из промежутка  , тогда получим  .

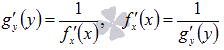Давайте проверим справедливость этих формул.

Найдем обратную функцию для натурального логарифма   (здесь y – функция, аx - аргумент). Разрешив это уравнение относительно x, получим   (здесь x – функция, а y – ее аргумент). То есть,   и   взаимно обратные функции.

Из таблицы производных видим, что   и  .

Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:

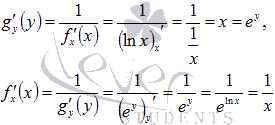
Как видите, получили такие же результаты как и в таблице производных.

Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.

Начнем с производной арксинуса.

Для   обратной функцией является  . Тогда по формуле производной обратной функции получаем

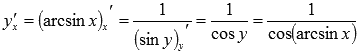
Осталось провести преобразования.

Так как областью значений арксинуса является интервал  , то   (смотрите раздел основные элементарные функции, их свойства и графики). Поэтому  , а   не рассматриваем.

Следовательно,  . Областью определения производной арксинуса является промежуток (-1; 1).

Для арккосинуса все делается абсолютно аналогично:

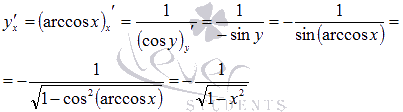
Найдем производную арктангенса.

Для   обратной функцией является  .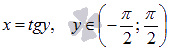

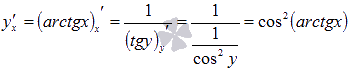
Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.

Пусть arctgx = z, тогда

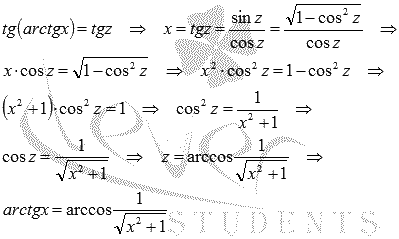
Следовательно,

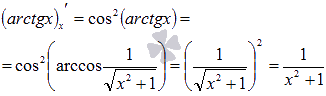
Схожим образом находится производная арккотангенса:

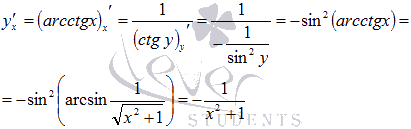
### 4)Производные неявной функции.

Несомненно, в нашем сознании образ функции ассоциируется с равенством   и соответствующей ему линией – графиком функции. Например,   - функциональная зависимость, графиком которой является квадратичная парабола с вершиной в начале координат и направленными вверх ветвями;   - функция синуса, известная своими волнами.

В этих примерах в левой части равенства находится y, а в правой части – выражение, зависящее от аргумента x. Другими словами, имеем уравнение, разрешенное относительно y. Представление функциональной зависимости в виде такого выражения называется явным заданием функции (или функцией в явном виде). И этот тип задания функции является для нас наиболее привычным. В большинстве примеров и задач нам предстают именно явные функции. Про дифференцирование функций одной переменной, заданных в явном виде, мы уже в деталях поговорили.

Однако, функция подразумевает соответствие между множеством значений величины x и множеством значений y, причем это соответствие НЕ обязательно устанавливается какой-либо формулой или аналитическим выражением. То есть, существует множество способов задания функции помимо привычного  .

В данной статье мы рассмотрим неявные функции и способы нахождения их производных. В качестве примеров функций, заданных неявно, можно привести   или  .

Как Вы заметили, неявная функция определяется соотношением  . Но не все такие соотношения между x и y задают функцию. Например, ни одна пара действительных чисел x иy не удовлетворяет равенству  , следовательно, это соотношение неявную функцию не задает.

 может неявно определять закон соответствия между величинами x и y, причем каждому значению аргумента x может соответствовать как одно (в этом случае имеем однозначную функцию) так и несколько значений функции (в этом случае функцию называют многозначной). К примеру, значению x = 1 соответствует два действительных значения y = 2 иy = -2 неявно заданной функции  .

Неявную функцию   привести к явному виду далеко не всегда возможно, иначе не пришлось бы дифференцировать сами неявные функции. Например,   - не преобразовывается к явному виду, а   - преобразовывается.

Теперь к делу.

Чтобы найти производную неявно заданной функции, необходимо продифференцировать обе части равенства   по аргументу x, считая y – функцией от x, и после этого выразить  .

Дифференцирование выражений, содержащих x и y(x), проводится с использованием правил дифференцирования и правила нахождения производной сложной функции. Давайте сразу подробно разберем несколько примеров, чтобы дальше не было вопросов.

17. Пусть функция y=f(x) дифференцируема на множестве Х. Производная f'(x) этой функции является функцией от х на Х. Следовательно, можно говорить о производной полученной функции, т.е. о производной от первой производной. Если она существует, то её называют производной второго порядка функции у= f(x) или , короче, второй производной и обозначают f''(x) или у''. Значит по определению f''(x)=( f' (x))'. Аналогично если существует производная от второй производной, то её называют третьей производной и обозначают f'''(x)=( f''(x))' и т.д. Вообще производной n-го порядка называют производную от производной (n-1)- го порядка 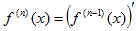и обозначают

18. 123

19. 123

20. Неопределённый интегра́л для функции — это совокупность всех первообразных данной функции.

21. 123

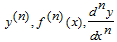
22. 123