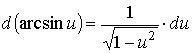Действия над векторами, заданными своими координатами

Если векторы заданы своими координатами в базисе e₁,  e₂ , e₃, то действия над ними выполняются по следующим правилам:

1.  При сложении двух (или большего числа) векторов  их  соответственные  координаты  складываются:

(x₁; y₁; z₁) + (x₂; y₂; z₂) = (x₁ + x₂;    y₁ + y₂;   z₁ + z₂).

В самом деле, для двух векторов (x₁; y₁; z₁)  и (x₂; y₂; z₂) имеем

(x₁; y₁; z₁) + (x₂; y₂; z₂) =

= (x₁e₁ + y₁e₂ + z₁e₃) + (x₂e₁ + y₂e₂ + z₂e₃) =

= (x₁ + x₂) e₁ + ( y₁ + y₂) e₂ + (z₁ + z₂) e₃ =

= (x₁ + x₂;    y₁ + y₂;   z₁ + z₂).

Для суммы трех или большего числа векторов доказательство проводится аналогично.

2.  При вычитании векторов их соответственные координаты вычитаются:

(x₁; y₁; z₁) — (x₂; y₂; z₂) = (x₁ — x₂;    y₁ — y₂;   z₁ — z₂)

3.  При умножении вектора на число все его координаты умножаются на это число.

В самом деле, для вектора  (x₁; y₁; z₁)  и числа λ, имеем

λ (x₁; y₁; z₁) = λ (x₁e₁ + y₁e₂ + z₁e₃) =

= (λ x₁)e₁+ (λ y₁)e₂ + (λ z₁)e₃ = (λx₁; λy₁; λz₁)

7. Уравнение прямой.

Прямая (прямая линия) - это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками. Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида:

Ax + By + C = 0 где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y = kx + b

где k - угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (a:0) и (0:b), то она может быть найдена используя формулу уравнения прямой в отрезках

x	+	y	= 1
a		b

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки A (x1;y1) и B (x2;y2) такие что x1≠x2 и y1≠y2, то уравнение прямой можно найти, используя следующую формулу: 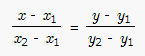Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом: где (x0;y0) - координаты точки лежащей на прямой, {l;m} – координаты направляющего вектора прямой. Каноническое уравнение прямой на плоскости

Если известны координаты точки A (x0;y0), лежащей на прямой, и направляющего вектора n = {l;m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

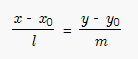
8. Эллипс и окружность. Эллипс – множество всех точек плоскости сумма расстояний от каждой точки которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами Фокусы эллипса обозначают буквам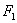и   и  , расстояние между ними - через 2с. По определению эллипса   или 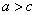 .  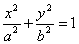(1) Уравнение (1) – каноническое уравнение эллипса 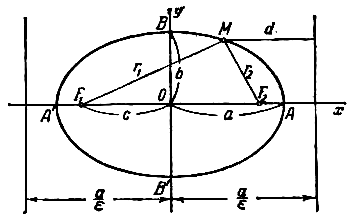При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии - просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса суть точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью.

Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае  ; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b - полуось, расположенную на оси Оу, независимо от того, что больше, a илиb. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.

- эксцентриситетом эллипса, где а - большая полуось. Очевидно,   (для окружности  ). Если М(x; y) - произвольная точка эллипса, то отрезки   и   (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам. ,  . Если эллипс определен уравнением (1) и  , то прямые ,  y - называются директрисами эллипса (если  , то директрисы определяются уравнениями  ,  . Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки эллипса до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса: - Уравнение эллипса со смещенным центром. Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Окружность можно рассматривать как частный случай эллипса, у которого полуоси = между собой, а => эксцентриситет = 0

9. Гипербола 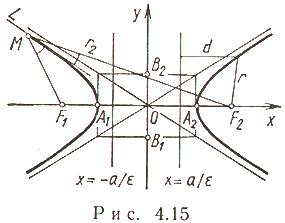Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.  Пусть расстояние между фокусам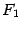и   и 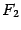  гиперболы равно 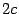  , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 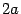  . Тогда гипербола в выбранной выше системе координат имеет уравнение 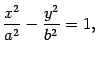- каноническое ур-ие. где

. Гипербола - множество точек M плоскости, для каждой из которых модуль разности расстояний от точек   и   равен 2a. Точки   и   называются фокусами гиперболы;   - действительная ось;   - мнимая ось; O - центр;   - левый и правый фокусы;   - вершины;   - фокальные радиусы: 

   Эксцентриситет: 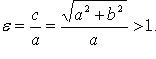  Фокальные радиусы:

       для правой ветви 

       для левой ветви 

     Фокальный параметр: 

     Уравнения директрис:   Основное свойство директрис:   где r - фокальный радиус любой точки гиперболы; d - расстояние от нее до соответствующей (односторонней) директрисы.

     Уравнение касательной в точке 

     Свойство касательной к гиперболе: 

     Уравнение нормали в точке 

     Уравнения асимптот: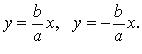 

     Уравнение гиперболы, сопряженной данной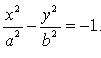 

     Уравнение равносторонней гиперболы:

     каноническое 

     отнесенное к осям как к асимптотам: 

     Уравнение диаметра (сопряженного хордам с угловым коэффициентом k):

10. Парабола 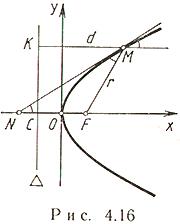Пусть на плоскости заданы точка F и прямая 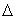 , не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой  . Точка F называется фокусом, прямая   - директрисой параболы; (OF) - ось, O - вершина, 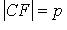  - параметр, 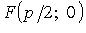  - фокус,   - фокальный радиус.

     Каноническое уравнение: 

     Эксцентриситет: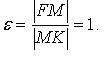 

     Фокальный радиус: 

     Уравнение директрисы: 

     Уравнение касательной в точке 

     Свойство касательной к параболе:   (М - точка касания; N - точка пересечения касательной с осью Ox).

     Уравнение нормали в точке 

     Уравнение диаметра, сопряженного хордам с угловым коэффициентом k: y = p/k.

     Параметрические уравнения параболы: 

11. Числовые последовательности и их пределы Последовательности.  Рассмотрим ряд натуральных чисел:

 

1,  2,  3, … ,  n –1,  n, … .

 

Если заменить каждое натуральное число  n  в этом ряду некоторым числом  u_n , следуя некоторому закону, то мы получим новый ряд чисел:          

 

u₁ ,   u₂ ,   u₃ , …,   u_n  1 ,   u_n  , …,  кратко обозначаемый { u_n }  

 

и называемый числовой последовательностью. Величина  u_n называется общим членом последовательности. Обычно числовая последовательность задаётся некоторой формулой  u_n = f ( n ), позволяющей найти любой член последовательности по его номеру  n ; эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов

Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу  a  приувеличении порядкового номера  n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгоеопределение. 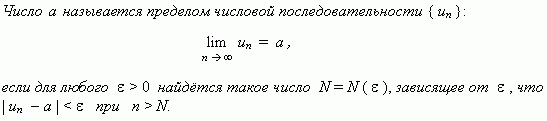Последовательность называется ограниченной, если существует такое число M, что | u_n  |  M для всех  n . Возрастающая или убывающая последовательность называется монотонной. Это определение означает, что  a  есть предел числовой последовательности, если её общий член неограниченно приближается к  a  при возрастании  n. Геометрически это значит, что для любого   > 0  можно найти такое число N,  что начиная с  n > N  все члены последовательности расположены внутри интервала ( a  a   ). Последовательность, имеющая предел, называется сходящейся; в противном случае –расходящейся.

12. Предел функции — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. Пишется .

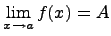
1. Предел суммы

Предел суммы равен сумме пределов, если каждый из них существует, т.е.

2. Предел разности

Предел разности равен разности пределов, если каждый из них существует, т.е.

3. Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

4. Предел произведения функции на постоянную величину

постоянный коэффициент можно выносить за знак предела: .

5. Предел произведения 

Предел произведения равен произведению пределов, если каждый из них существует, т.е.

6. Предел частного

Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.

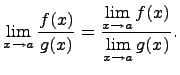
7. Предел степенной функции

где степень p - действительное число.

8. Предел показательной функции

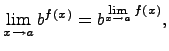где основание b > 0.

9. Предел логарифмической функции

где основание b > 0.

13. Теорема 1. Сумма непрерывных функций есть функция непрерывная.  Доказательство. Пусть функци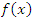и     и 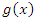    непрерывны в точке  a. Тогда

Согласно свойству пределов функций существование пределов функций     и     гарантирует существование предела их суммы. При этом

что и требовалось доказать.  Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная.  Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция.

Теорема 2. Произведение непрерывных функций есть функция непрерывная.  Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная.  Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль.  Доказательство теорем 2 и 3 по своей сути не отличается от доказательства теоремы 1 и предоставляется читателю.

Теорема 4. Любая элементарная функция непрерывна в области своего определения.  Для доказательства этой теоремы нужно показать, что для любого числа  a  из области определения элементарной функции     выполняется условие

Продемонстрируем справедливость теоремы на некоторых конкретных примерах. Пусть   , где  n  – целое положительное число. Тогда

 

Первый член в правой части этого равенства представляет собой бесконечно малую функцию при  x → a  и, следовательно, Покажем, что показательная функция  является непрерывной в каждой точке  a. Действительно,    

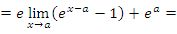
Теорема 5. Пусть функция     непрерывна на промежутке [a,b] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка  c, в которой   .  Действительно, непрерывность функции на некотором промежутке означает отсутствие скачков функции на этом промежутке. Другими словами,     принимает все значения, заключенные между ее минимальным и максимальным значениями на промежутке [a,b], одним из которых является нулевое значение. 

14. Производная и дифференциал. Производная высших порядков.

Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференцированием. Обратный процесс — нахождение первообразной — интегрирование.

Дифференциалом функции называется линейная часть приращения функции относительно приращения аргумента Δ f = A·Δx + o(Δx), то есть df = A·Δx.

Связь дифференциала функции с её производной

Дифференциал функции равен произведению производной функции на приращение аргумента dy = f '(x)·Δx. В данном случае A = f ' (x).  Действительно,

.

Дифференциал есть функция двух переменных, он зависит от аргумента x и приращения Δ x. Если считать, что y = x, то по определению дифференциала функции dx = 1·Δ x. Значит, dx = Δ x и dy = f ' (x)· Δ x.

Геометрический смысл дифференциала.

Построим график функции y = f (x). В точке M(x, f (x))  проведем касательную MT. Как известно, tg α = f ' (x), из Δ ТМР имеем TP = MP· tg α, MP = Δ x = dx, поэтому

TP = f '(x)·dx = dy.

Дифференциал функции есть приращение ординаты касательной.    Замечание. Из определения дифференциала следует, что производная функции равна отношению дифференциала функции к дифференциалу ее аргумента

.

Таблица дифференциалов.

1	d(u + v) = du + dv	2	d(u·v) = v·du + u·dv
3		4	d(sin u) = cos u·du
5	d(cos u) = − sin u·du	6
7		8
9	d(eu) = eu·du	10
11		12
13		14
15		16