16. Public key crypto. Rsa
RSA gets its security from the difficulty of factoring large numbers. The public and private keys are functions of a pair of large prime numbers. Recovering the plaintext from the public key and the ciphertext is conjectured to be equivalent to factoring the product of the two primes.To generate the two keys, choose two random large prime numbers, p and q. Compute the product: n = pq. Then randomly choose the encryption key, e, such that e and (p - 1)(q - 1) are relatively prime.
Finally,
use the extended Euclidean algorithm to compute the decryption key,
d,
such thated=1mod(p-1)(q-1)In other words, d=
mod((p-1)(q-1))Note
that d
and
n
are
also relatively prime. The numbers e
and
n
are
the public key; the number d
is
the private key. The two primes, p
and
q,
are no longer needed. That is, if both p
and
q
are
100-digit primes, then n
will
have just under 200 digits and each message block, mi
, should be just under 200 digits long. The encrypted message, c,
will be made up of similarly sized message blocks, ci,
of about the same length. The encryption formula is simply
modnTo
decrypt a message, take each encrypted block ci
and compute
modn
Since
the formula recovers the message. The message could just as easily
=
=
=
=
=
*1=
;
all mod n
have been encrypted with d and decrypted with e; the choice is arbitrary.
RSA Encryption
Public Key:nproduct of two primes, p and q (p and q must remain secret)e relatively prime to (p- 1)(q - 1)
Private Key:d mod((p-1)(q-1))
Encrypting:c=
mod
n
Decrypting:m=
mod
n
17 Public key crypto.Diffie-Hellman
Diffie-Hellman was the first public-key algorithm ever invented, way back in 1976 It gets its security from the difficulty of calculating discrete logarithms in a finite field, as compared with the ease of calculating exponentiation in the same field. Diffie-Hellman can be used for key distribution—Alice and Bob can use this algorithm to generate a secret key—but it cannot be used to encrypt and decrypt messages. The math is simple. First, Alice and Bob agree on a large prime, n and g, such that g is primitive mod n. These two integers don’t have to be secret; Alice and Bob can agree to them over some insecure channel. They can even be common among a group of users. It doesn’t matter.
Then, the protocol goes as follows:
(1) Alice chooses a random large integer x and sends Bob
X =
mod
n
(2) Bob chooses a random large integer y and sends Alice
Y =
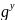mod
n
(3) Alice computes
k =
mod
n
(4) Bob computes
k´ =
mod
n
Both k
and
k´
are
equal to
mod
n.
No
one listening on the channel can compute that value; they
only know n, g, X, and Y. Unless they can compute the discrete logarithm and recover x or y, they do
not solve the problem. So, k is the secret key that both Alice and Bob computed independently.
The choice of g and n can have a substantial impact on the security of this system. The number (n -1)/2 should also be a prime .And most important, n should be large: The security of the
system is based on the difficulty of factoring numbers the same size as n. You can choose any g,
such that g is primitive mod n; there’s no reason not to choose the smallest g you can—generally a
one-digit number. (And actually, g does not have to be primitive; it just has to generate a large
subgroup of the multiplicitive group mod n.)
18.Linearcryptanalysisis another type of cryptanalytic attack, invented by Mitsuru Matsui in 1993-4.
This attack uses linear approximations to describe the action of a block cipher .
This means that if you XOR some of the plaintext bits together, XOR some ciphertext bits together,
and then XOR the result, you will get a single bit that is the XOR of some of the key bits. This is a
linear approximation and will hold with some probability p.If p неравно ½, then this bias can be
exploited. Use collected plaintexts and associated ciphertexts to guess the values of the key bits. The
more data you have, the more reliable the guess. The greater the bias, the greater the success rate
with the same amount of data.
Example:
Given:
Find:
+
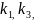
S block
S
block
=
+
=
+
+
=
+
=
+
=
+
=
+
+
=
+
+
+
+
=
+
+
+ +P2= + +
+ +P2=
+ +P0= + +
= + +
C2+P1=P1+k1+C0+C1+P1
C2+P1+C0+C1=k1+C0+C1+C0+C1
K1=P1+C0+C1+C2
Answear: = + + , K1=P1+C0+C1+C2
+ +P2= ,
19.Differential cryptanalysis is a general form of cryptanalysis applicable primarily to block ciphers, but also to stream ciphers and cryptographic hash functions. In the broadest sense, it is the study of how differences in an input can affect the resultant difference at the output. In the case of a block cipher, it refers to a set of techniques for tracing differences through the network of transformations, discovering where the cipher exhibits non-random behaviour, and exploiting such properties to recover the secret key.
The main difference from linear attack is that differential attack involves comparing the XOR of two inputs to the XOR of the corresponding outputs.
Differential attack is a chosen-plaintext attack.
We consider inputs x and x* having a specified XOR value denoted by .
We decrypt y and y* using all possible key and determine if their XOR has a certain value. Whenever it does, increment the corresponding counter. At the end, we expect the largest one is the most likely subkey.
;
Example: P
+
k
C
P,C-known
k-?
P+C
C=P+k
C+P=P+K+P=K