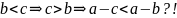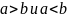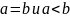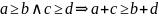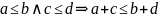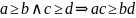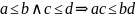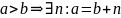- •1.Множество натуральных чисел n. Аксиомы Пеано
- •2.Независимость аксиом Пеано
- •3. Принцип полной математической индукции. Обобщенный принцип полной математической индукции. Примеры доказательства методом математической индукции
- •4. Сложение натуральных чисел как бинарная алгебраическая операция и как функция. Примеры. Свойство сокращения
- •5. Теорема о сложении натуральных чисел: единственность
- •6. Теорема о сложении натуральных чисел: существование
- •7.Ассоциативность сложения натуральных чисел
- •8. Коммутативность сложения натуральных чисел
- •Существование:
- •23. Частное натуральных чисел: определение и единственность. Свойства частного натуральных чисел
- •26. Свойства сложения и вычитания для натуральных чисел: .
- •27. Суммы и произведения нескольких натуральных чисел. Обобщенный закон дистрибутивности. Степень натурального числа с натуральным показателем и ее свойства
- •28. Равномощные множества. Отношение эквивалентности «быть равномощным». Отрезок натурального ряда. Конечные и бесконечные множества
- •29. Теорема о равномощности конечного множества только одному отрезку натурального ряда
- •30. Лемма о наибольшем и наименьшем элементе в конечном множестве. Бесконечность множества натуральных чисел
- •31. Счетность множеств целых и рациональных чисел. Несчетность множества действительных чисел
- •32. Отношение эквивалентности на множестве n2. Определение целого числа как класса эквивалентности на n2. Примеры
- •33. Определение суммы целых чисел и его корректность
- •34. Свойство сложения целых чисел
- •35. Определение произведения целых чисел и его корректность. Кольцо целых чисел и его свойства
- •38. Вложение множества натуральных чисел в кольцо целых чисел. Множество положительных целых чисел: определение, корректность определения, описание
- •40. Целое число как разность двух натуральных чисел. Отрицательные и положительные числа. Архимедовость и дискретность кольца целых чисел
- •41. Определение рациональных чисел как классов эквивалентности
- •42. Определение суммы рациональных чисел и его корректность. Аддитивная абелева группа рациональных чисел
- •43. Определение произведения рациональных чисел и его корректность. Поле рациональных чисел.
- •46. Вложение кольца целых чисел в поле рациональных чисел. Изоморфизм колец
- •47. Рациональное число как частное двух целых чисел. Поле рациональных как наименьшее поле, которое содержит кольцо целых чисел
- •49. Представление бесконечных периодических десятичных дробей обыкновенными дробями: правило, примеры
- •50. Определение действительных чисел как бесконечных десятичных дробей. Множество конечных десятичных дробей. Подходящие дроби
- •51. Определение и свойства отношения порядка на множестве действительных чисел
- •52. Плотность множества д в множестве действительных чисел
- •53. Определение и свойство суммы и произведения действительных чисел. Поле действительных чисел и его свойства
- •54. Определение, свойства и алгебраические операции с комплексными числами
- •55. Определение кватернионов. Алгебраические операции над кватернионами. Тело кватернионов
- •56. Вложение поля комплексных чиселв тело кватернионов. Теорема Фробениуса
Существование:
Fix(a); ММИ по b
b=1:

Пусть
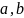 выполняется одно из соотношений 1,2,3.
Докажем, что
выполняется одно из соотношений 1,2,3.
Докажем, что
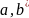 тоже выполняется одно из трёх соотношений.
тоже выполняется одно из трёх соотношений.
Пусть
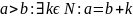
Если
k=1,
то
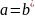 (соотношение
2)
(соотношение
2)
Если
k>1,
то
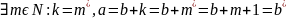 +m,
+m,
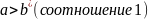
Если
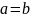 ,
значит
,
значит
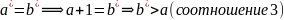
Если
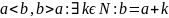
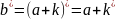
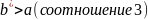
15. Отношение «>» как отношение строгого порядка на множестве N. Свойство трихонометрии: единственность
Опр.1. Пусть , будем говорить, что , если , что
Свойство 1:
Док-во: ч.т.д.
Теорема_1(сво-во трихотомии): имеет место только одно из соотношений:
Док-во:
Докажем, что никакие два соотношения 1,2,3 не выполняются одновременно.
Пусть
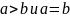
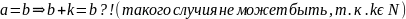
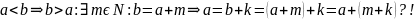
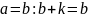
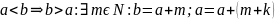
16. Отношение «>» как отношение порядка на множестве N.
Опр.4.: Отношение R на множестве M называется отношением порядка, если оно:
Рефлексивно (
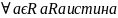 )
)Антисимметричность (
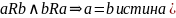
Транзитивность:
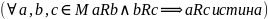
Теорема
3:
Отношение
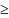 является отношением порядка на
является отношением порядка на
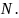
Док-во: 1,2 – очевидно.
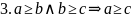
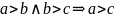
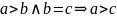
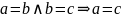 ч.т.д.
ч.т.д.
Сво-во
2:

Док-во: ММИ по a
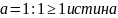
Пусть
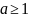 .
Докажем, что
.
Докажем, что
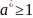 :
по свойству 1:
:
по свойству 1:
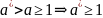
ч.т.д.
17. Отношение «>» как отношение линейного порядка на множестве N.
Опр.4:
Отношение порядка R
на множестве
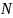 называется линейным,
если
называется линейным,
если
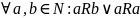 .
.
Теорема
4:
Отношение
является отношением линейного порядка
на множестве
:
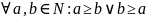 .
.
Док-во:
Fix(b); ММИ по a
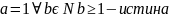
пусть
для a
выполняются следующее:
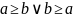 .Докажем,
что
.Докажем,
что
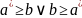 .
.
Если
,
то
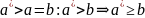
Если
,
то

Если
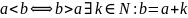
Если
k=1,
то
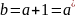
Если
k>1,
то
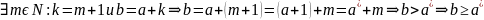
ч.т.д.
18. Закон монотонности сложения на множестве N и следствия из него
Теорема
5:
(закон монотонности сложения):
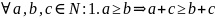
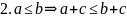
Док-во:
1. (
)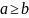
Если
,
то
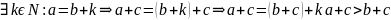
Если

(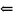 )
)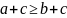
Пусть
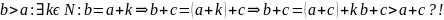
2. аналогично.
ч.т.д.
Следствие:
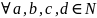
19. Закон монотонности умножения на множестве N и следствия из него
Теорема
6:
(закон монотонности умножения):


Следствие:
20. Дискретность и архимедовость множества натуральных чисел
Сво-во:
(архимедовасть множества
чисел):
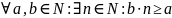
Док-во:
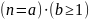
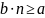
ч.т.д.
Сво-во:
(дискретность множества
чисел):

Док-во:

ч.т.д.
21. Разность натуральных чисел: определение и единственность. Условие существования разности натуральных чисел
Опр.:
Натуральное число
 (если оно
(если оно
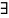 )
называется разностью чисел
)
называется разностью чисел
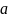 и
,
если
и
,
если
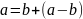 .
.
Замечание:
Разность
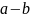 есть решение уравнения
есть решение уравнения
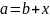 .
.
Теорема 1:
 ;
;Если разность , то она определена единственным образом.
Доказательство:
пусть

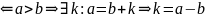 ;
;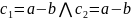
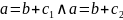
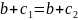
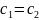 .
.
22. Свойства разности натуральных чисел
Теорема 2:
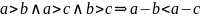 ;
;
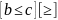
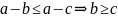 .
.
Доказательство:

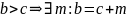

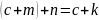
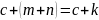
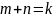
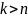
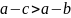 ;
;
Пусть