22Дисперсия альтернативного признака.

Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:

Подставляя в данную формулу дисперсии q =1- р, получаем:

23Виды дисперсии и правило их сложения.

Расчет групповой, межгрупповой и общей дисперсии

Если совокупность разбита на группы (или части) по изучаемому признаку, то для такой совокупности могут быть исчислены следующие виды дисперсий: общая, групповая, средняя из групповых, межгрупповая.

Общая дисперсия отражает вариацию признака за счет всех условий и причин, действующих в совокупности, и исчисляется по формуле:

— простая дисперсия;

— взвешенная дисперсия.

Общая дисперсия равна среднему квадрату отклонений отдельных значений признака x от общей средней величины .

Групповая (частная) дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы (групповой средней). Эта дисперсия отражает вариацию признака только за счет условий и причин, действующих внутри группы:

— простая;

— взвешенная.

Средняя из групповых дисперсий — это средняя арифметическая взвешенная из групповых дисперсий:

.

Ее называют остаточной.

Межгрупповая дисперсия равна среднему квадрату отклонений групповых

средних от общей средней и обозначается (малая сигма):

.

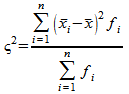определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию). Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий.

24Сущность выборочного наблюдения. .

В статистике сравнительно редко встречается такой сплошной вид наблюдения, как всеобщая перепись населения. Чаще приходится использовать несплошные наблюдения, когда из совокупности необходимо выбирать какую-то часть единиц и на основании ее обследования давать характеристику всем статистическим единицам совокупности. Выборочное наблюдение — это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц совокупности осуществляется случайно, отобранная часть подвергается обследованию, после чего результаты распространяются на всю исходную совокупность.

К использованию выборочного метода (или выборки) прибегают в различных случаях, когда само наблюдение связано с порчей или уничтожением наблюдаемых единиц (например, при контроле качества: испытание пряжи на крепость, консервов на доброкачественность). Когда сплошное наблюдение нельзя осуществить из-за большого объема совокупности, когда исследование нужно провести в сжатые сроки при небольших затратах и др.

25Виды и способы отбора единиц в выборочную совокупность. Совокупность отобранных для обследования единиц называют выборочной, а совокупность единиц, из которой производится отбор,— генеральной.

По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности; при групповом отборе — качественно однородные группы; комбинированный отбор предполагает сочетание первого и второго видов. По методу отбора различают повторную и бесповторную выборки. При повторной выборке общая численность единиц генеральной совокупности остается неизменной, так как единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность. При бесповторной выборке численность единиц генеральной совокупности сокращается. Единица совокупности в дальнейшем в выборке не участвует и в генеральную совокупность не возвращается. Способом отбора определяется механизм или процедура выборки единиц. Различают следующие виды выборки: собственно-случайная, механическая, типическая, серийная и комбинированная. К собственно-случайной выборке относится отбор единиц посредством жеребьевки, лотереи. Механическая выборка состоит в том, что отбор единиц осуществляется в определенном порядке (например, по алфавиту, в порядке возрастания или убывания значений какого-либо показателя, не связанного с изучаемым свойством), отбирается число единиц механически, через определенный интервал. Типическая выборка применяется для отбора единиц из неоднородной совокупности. Генеральная совокупность разбивается на несколько однородных групп по признакам и из каждой группы собственно-случайной или механической выборкой производится отбор единиц в выборочную совокупность. Серийная выборка — это отбор равновеликих групп (серий, гнезд).