17Сущность и значение средних величин.

Среди обобщающих показателей, характеризующих общественные явления, большое значение имеют средние величины.

Средние величины исчисляют для того, чтобы дать сводную обобщающую характеристику всей совокупности или группы общественных явлений по одному какому-то признаку. Размер заработной платы у рабочих одной профессии может быть различным, но в то же время в данных конкретных условиях места и времени существует какой-то характерный размер их заработка в отличие от заработка других профессий. Средняя величина представляет собой обобщающую характеристику единиц совокупности по какому-либо варьирующему признаку. Основой для получения правильных средних является научная группировка статистических материалов, в результате которой получаются однородные данные по тому или иному группировочному признаку. Итак, средняя может служить обобщенной характеристикой совокупности только тогда, когда совокупность состоит из однотипных единиц. Если же средние исчисляются для разнокачественных, разнотипных явлений, то они теряют реальный смысл. Статистика устанавливает следующие принципы научного применения метода средних величин: Прежде чем исчислять среднюю величину, необходимо тщательно проанализировать состав совокупности.

Не следует исчислять средние только для совокупности в целом, а надо широко использовать групповые средние для отдельных частей совокупности. Необходимо правильно выбирать вид средней величины.

Средние величины делятся на два класса: Степенные средние (арифметическая, гармоническая, геометрическая, квадратическая, кубическая). Структурные (мода, медиана). Степенные средние объединяются общей формулой (при различных значениях m):

,

где — среднее значение исследуемого явления;  m — показатель степени средней; х — текущее значение осредняемого признака; n — число признаков.

18.Средняя арифметическая, ее методы расчета. Наиболее распространенным видом средних величин является средняя арифметическая, которая в зависимости от характера имеющихся данных может быть простой и взвешенной. Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по несгруппированным данным. В общем виде формулу простой арифметической можно записать так:

,

где — средняя величина (читается «икс с чертой»); х — индивидуальные значения величины признака (варианты); n — число единиц совокупности (частоты или веса); Σ — знак суммирования (буква греческого алфавита — «сигма»).

При расчете средних величин отдельные значения признака могут повторяться, встречаться по нескольку раз. В этом случае используется средняя арифметическая взвешенная величина. Формулу средней арифметической величины можно записать так:

,

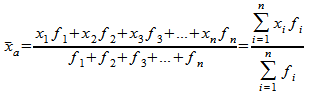где f — частоты.

Итак, если отдельные значения признака (варианты) повторяются в совокупности по нескольку раз, то исчисляется средняя арифметическая взвешенная. Чтобы ее определить, надо: варианты умножить на соответствующие частоты (веса); произведения сложить; сумму произведений разделить на сумму частот.

Простая средняя арифметическая величина — частный случай средней арифметической взвешенной. Средняя арифметическая величина обладает многими математическими свойствами. Знание этих свойств помогает контролировать правильность и точность расчета средней варианты, способствует упрощению расчетов. Алгебраическая сумма отклонений индивидуальных вариант от среднего значения равна нулю. На практике часто приходится исчислять среднюю величину для интервального вариационного ряда. В интервальных рядах значение вариант дано в виде интервала «от… до…». Поэтому для расчета средней надо, прежде всего, освободиться от интервалов, т. е. по каждой группе исчислять среднее значение интервала. Среднее значение интервала находят как полусумму его верхней и нижней границ. После того как найдено среднее значение интервалов, их умножают на частоты (веса) и сумму произведений делят на сумму частот (весов), т. е. так же, как исчисляется средняя арифметическая взвешенная. Пример. Имеются данные группировки заводов по стоимости готовой продукции. Необходимо определить среднюю стоимость готовой продукции на один завод.

№ групп	Группы заводов по стоимости готовой продукции, млн. долл.	Число заводов
1	до 2	10
2	2 – 3	20
3	3 – 4	30
4	4 – 5	25
5	5 – 6	10
6	свыше 6	5
Итого:		100

Решение. Для исчисления средней в интервальном ряду нужно, прежде всего, получить середину интервала каждой группы.

Для второй группы и т. д.

Имеются интервалы с так называемыми открытыми границами в первой и шестой группах (до 2 и выше 6). В таких случаях берется значение последующего интервала (для первого ) и определяется размер интервала и нижняя его граница (нижняя граница) — среднее значение для первой группы. И для последней группы размер интервала в предыдущей группе (5-й) . Определяем верхнюю границу шестого интервала . Определяем середину 6-й группы: — середина интервала шестой группы.

После того, как найдено среднее значение интервалов, расчет производится по формуле средней арифметической взвешенной:

.

Расчет средней стоимости готовой продукции на один завод:

№ групп	Группы заводов по стоимости готовой продукции, млн. долл.	Число заводов, f	Среднее значение интервала и расчет его , млн. долл., х	Произведение вариант на частоты , млн. долл., xf
1	до 2	10		15
2	2 – 3	20		50
3	3 – 4	30		105
4	4 – 5	25		112,5
5	5 – 6	10		55
6	свыше 6	5		32,5
Итого:

. Таким образом, мы рассчитали, что 3,7 млн. долл. в среднем приходится на один завод из 100. Одна из разновидностей средней арифметической величины — средняя хронологическая. Если числовые значения (варианты) известны на определенные периоды времени — моменты с равными промежутками времени, то средняя величина исчисляется по формуле средней хронологической:

.

Пример. Определить среднюю годовую стоимость нормируемых оборотных средств за год, если известны их остатки на первые числа месяца (млн. руб.):

Январь     — 520 Февраль   — 540 Март          — 535 Апрель      — 525 Май            — 570 Июнь         — 560 Июль         — 520 Август       — 550 Сентябрь — 510 Октябрь    — 530 Ноябрь     — 560 Декабрь   — 580

Январь следующего года — 540

Решение.

В тех случаях, когда необходимо определить средний уровень моментного ряда динамики с неравными промежутками между моментами, обычно используют формулу средней арифметической взвешенной величины.

Перепечат

19 Средняя гармоническая и другие виды средних. Обусловленность выбора средней характером исходной информации. Одной из видов средней является средняя гармоническая величина. Название ее неслучайно, так как эта средняя «гармонирует» со средней арифметической величиной. Средняя гармоническая — это величина, обратная средней арифметической из обратных значений признака. Иногда бывают известны лишь сведения о значении признака и его общем объеме, а число единиц неизвестно. В зависимости от характера анализируемого материала ее применяют тогда, когда веса приходится не умножать, а делить на варианты или умножать на обратное их значение. Различают среднюю гармоническую простую и взвешенную. Средняя гармоническая простая определяется по формуле

Применяется она тогда, когда вес (частота) каждого варианта равен единице. К средней гармонической простой прибегают для определения средних затрат труда, времени, материалов на единицу продукции по двум, трем, четырем и так далее предприятиям. Пример. Три промышленных предприятия заняты производством миксеров. Себестоимость миксера на первом предприятии — 5 у.е., на втором — 3 у.е., на третьем — 6 у.е. Определить среднюю себестоимость миксера. Решение. Используя формулу средней гармонической простой, определяем:

Формулу средней гармонической можно записать так:

, где х — отдельные варианты; Т — веса.

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин. Для определения среднего темпа роста используют среднюю геометрическую:

невзвешенную:,

где k — количество осредняемых величин; взвешенную:.

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения. В экономической практике иногда возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. В таких случаях применяется средняя квадратическая (например, для вычисления средней величины стороны квадратных участков, средних диаметров труб и т. п.) и средняя кубическая (например, при определении средней длины стороны n кубов) Средняя квадратическая простая является квадратным корнем из частного от делений суммы квадратов отдельных значений признака на их число:

Средняя квадратическая взвешенная:

В статистической практике находят применение средние 3-го и более высоких порядков.

20 Мода и медиана, способы их вычисления. Средние, о которых шла речь в предыдущих параграфах данной темы, являются обобщающими статистическими характеристиками изучаемого массового явления (совокупности) по тому или иному варьирующему признаку и одновременно своего рода абстракцией. Они отражают то общее, что присуще всем единицам совокупности. При этом может случиться, что величина средней не имеет точного равенства ни с одним из конкретных встречающихся в совокупности вариантов (значений единиц совокупности по признаку). Среднее число членов семьи равно 3,81. Дробного числа членов семьи не может быть. Средняя показывает некоторое центральное значение, около которого группируются реально существующие варианты. Поэтому наравне со средними в качестве общих статистических характеристик изучаемого признака могут быть использованы величины конкретных вариантов, занимающих в ранжированном (построенном в прядке возрастания или убывания) ряду индивидуальных значений признака определенное положение. В статистических исследованиях в качестве вспомогательных описательных статистических характеристик распределения варьирующего признака широко применяются мода и медиана. Модой в статистике называется величины признака (варианта), которая чаще всего встречается в данной совокупности. Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам. Обозначают медиану символом . Определение моды и медианы в дискретном ряду, где значения признака заданы определенными числами, не представляет большой трудности. В рассмотренном примере наиболее часто встречаются семьи, имеющие 4 члена семьи, т.е. =4 (семья имеющая 4 члена семьи). Могут быть распределения, где все варианты встречаются одинаково часто. В этом случае моды нет. В других случаях не одна, а две варианты могут иметь наибольшие частоты. Тогда у признака будут две моды и распределение будет бимодальным. Чтобы найти медиану в дискретном ряду, нужно сумму частот разделить пополам и к полученному результату добавить Такой номер семьи делит ряд пополам. Поскольку частоты с дробным номером не бывают, то медиана находиться посредине между 50-й и 51-й частотами. Затем по накопленным частотам (частостям) определяют величину варианта (признака), обладающего таким номером. Однако если единиц (частот) в совокупности достаточно много и различия между величинами рядом стоящих членов ряда небольшие, то можно считать медианой (с достаточной степенью точности) один из центральных вариантов с порядковым номером n/2. Так обычно поступают, определяя медиану при четном числе членов ряда. Рассмотрим, как определяется мода и медиана для интервального ряда. Прежде закрывают открытые интервалы (первый и последний) и определяют интервалы, в которых находятся мода и медиана. Их называют соответственно модальным и медианным интервалом. Модальный интервал – интервал с наибольшей частотой. В приведенном ниже примере, модальным является интервал 170-175 см. Для расчета определенного значения модальной величины признака, заключенного в этом интервале, применяют формулу. Смысл этой формулы заключается в следующем: величину той части модального интервала, которую нужно добавить к его минимальной границе, определяют в зависимости от величины частот предшествующего и последующего интервалов. Медианный интервал (содержащий частоту, который делит ряд пополам) определяется по накопленным частотам. Это будет интервал, накопленная частота которой равна или превышает половину суммы частот. Отсюда медианным интервалом будет интервал со значением роста от 170 до 175 см. До этого интервала сумма накопленных частей составила 175. Следовательно, чтобы получить значение медианы, необходимо прибавить 75 [или 76 единиц] (250,5-75). При определении значения медианы предполагают, что значение признака в границах этого медианного интервала распределяется равномерно. Прибавив полученную величину к минимальной границе интервала, получим искомую величину медианы. т.е. половина студентов имеет рост меньше 172.9 см, а вторая половина – больше. Строго говоря, приведенная формула моды пригодна только для рядов с равными интервалами. Формула медианы применима для любого интервального ряда. Определим среднюю арифметическую для второго примера. Для первого примера имеем: средняя = 3,81; мода = 4; медиана = 4 члена семьи. Для второго примера: средняя = 172,85; мода равна 173.3 и медиана = 172.9 см. Соотношение этих трех величин указывает направление и степень ассиметрии рядов распределения. мода и медиана является важными дополнительными характеристиками к средней изучаемой совокупности. Особенно ценны эти показатели для характеристик небольших по численности совокупностей. При этом следует помнить, что мода и медиана являются описательными статистическими характеристиками, т.к. в них не погашаются индивидуальные отклонения, они всегда соответствуют определенной варианте. В то же время можно привести немало примеров, когда мода или медиана являются более эффективной характеристикой, чем средняя. Например, при статистических методах контроля качества продукции, при оценке качества передачи информации, надежности работы средств труда широкого применяются мода и медиана. Так, таксофон, почтовый ящик следует разместить не на середине улицы, а в точке, которая делит численность проживающих пополам. Используется медиана. Показатель «вероятность безотказной работы» оценивается модой. Считается, что медиана по своему положению более определена, чем мода.

21Статистическое изучение вариации. Показатели вариации и методы их расчета. Средняя величина не раскрывает строения совокупности, она не показывает, как располагаются около нее варианты осредняемого признака. Исследование вариации в статистике дает возможность оценить степень воздействия на признак других варьирующих признаков. Вариация — это различие в значениях какого-либо признака у различных единиц совокупности в один и тот же период времени. Вариация существует в пространстве — это колеблемость значений признака по отдельным территориям и во времени — изменение значений признака в различные периоды времени. Исследование вариации помогает познать сущность изучаемого явления. Для измерения вариации признака в совокупности применяют ряд обобщающих показателей:

размах вариации; коэффициент осцилляции; среднее линейное отклонение;

средний квадрат отклонений (дисперсия); среднее квадратическое отклонение; коэффициент вариации. Наиболее простым измерителем вариации является разность между наибольшим и наименьшим значением признака и называется размах вариации и исчисляется по формуле:

,

где     R — размах вариации; — наибольшее значение признака;  — наименьшее значение признака.

Показатель вариации учитывает крайние значения признака, которые сильно могут отличаться от всех других единиц, поэтому иногда пользуются показателем осцилляции:

,

где K — коэффициент осцилляции; R — размах вариации;

— средняя арифметическая этого ряда.

Среднее линейное отклонение представляет среднюю арифметическую из абсолютных значений отклонений отдельных вариаций (значений признака) от их средней арифметической (знаки отклонений не учитываются). Среднее линейное отклонение может быть простым и взвешенным и измеряется в тех же единицах, что и величина признака. Вычисление среднего линейного отклонения производится по формулам:

для несгруппированных данных:

,

где — среднее линейное отклонение; x — значениe признака; — среднее значение признака; n — численность признаков.

;

если данные наблюдения представлены в виде дискретного ряда распределения с частотами, тогда:

.

Число повторений вариантов значений признака, называют частотой повторений. Если частоты представлены в относительных величинах, то их называют частостями.

Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от общей средней величины. Дисперсия еще называется средним квадратом отклонений и обозначается (сигма квадрат). В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:

— простая дисперсия;

— взвешенная дисперсия.

Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается (сигма):

— простое (невзвешенное квадратическое отклонение) среднее;

— среднее квадратическое отклонение взвешенное.

Среднее квадратическое отклонение — это обобщающая характеристика абсолютных размеров вариации признака в совокупности и выражается в тех же единицах измерения, что и сам признак (в метрах, тоннах, гектарах и т. д.). Вычислению среднего квадратического отклонения предшествует расчет дисперсии. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. В практике часто возникает необходимость сравнения вариаций различных признаков, например, вариаций возраста рабочих и их квалификации; стажа работы и производительности труда; себестоимости и прибыли и т. д. Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют коэффициент вариации. Коэффициент вариации — это отношение среднего квадратического отклонения к средней

арифметической:

%.

В отличие от среднего квадратического отклонения коэффициент вариации является относительной величиной, что используется при сравнении вариаций любых совокупностей. По величине коэффициента вариации можно судить о степени вариации признаков совокупностей. Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее явление. И чем больше его величина (V), тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.