§ 1.4. Теория винтовой пары

Зависимость между моментом, приложенным к гайке, и осевой силой винта. Если винт нагружен осевой силой Т⁷ (рис. 1.13), то для завинчивания гайки к ключу необходимо приложить момент Г_зав, а к стержню винта — реактивный момент Г_р, который удерживает стержень от вращения. При этом можно записать

т_м=ъ+т_р, (1.3)

где Т_т — момент сил трения на опорном торїіе гайки; Т_р— момент сил трения в резьбе. Равенство (1.3), так же как и последу­ющие зависимости, справедливо для любых винтовых пар бол­тов, винтов, шпилек и винтовых механизмов.

Рис. 1.13

в)	\п	1 ^^1
\Ft	/
Vf	/
	f ]	чЛ
	Рис. 1.14

Не допуская существенной по­грешности, принимают приведен­ный радиус сил трения на опорном торце гайки равным среднему радиусу этого торца или Д.р/2. При этом

T_T = Ff(DJ 2), (1.4)

где D_cp=(D₁+d_OTB)l2; D_{—наружный диаметр опорного торца гайки; d_0TB — диаметр отверстия под винт; /—коэффициент трения на торце гайки.

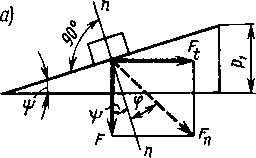
Момент сил трения в резьбе определим, рассматривая гайку как ползун, поднимающийся по виткам резьбы, как по наклонной плоскости (рис. 1.14, а). По известной теореме механики, учи­тывающей силы трения, ползун находится в равновесии, если равнодействующая F_n системы внешних сил отклонена от нормали п — п на угол трения ср. В нашем случае внешними являются осевая сила F и окружная сила F_t = 2T_p/d₂- Здесь Г_р—не реактивный, а активный момент со стороны ключа, равный T_iaB—T_r [см. формулу (1.3)].

Далее (рис. 1.14), F, = Ftg(\(/ + <p) или

r_p = 0,5Mtg(*|/ + <p), (1-5)

где \|/—угол подъема резьбы [по формуле (1.1)]; <p = arctg/_np — угол трения в резьбе; /_пр — приведенный коэффициент трения в резьбе, учитывающий влияние угла профиля [формула (1.2)].

Подставляя значения моментов в формулу (1.3), найдем искомую зависимость:

Г,_ав = 0,5Fd₂ [{DJd₂)f+ tg (i|/ + ф)]. (1.6)

При отвинчивании гайки окружная сила F_t и силы трения меняют направление (рис. 1.14,6). При этом получим

(1.7)

Момент отвинчивания с учетом трения на торце гайки, по аналогии с формулой (1.6),

Г_отв = 0,5 Л/₂ [(/>_ср/</₂)/+ (_Ф - *)]. (1.8)

Полученные зависимости позволяют отметить:

1. По формуле (1.6) можно подсчитать отношение осевой силы винта Г к силе приложенной на ручке ключа, т. е. F/F_I(, которое дает выигрыш в силе. Для стандартных метрических резьб при стандартной длине ключа 1к\5с1 и /«0,15 F/i^г_1[ = 70...80 (см. табл. 1.6).

2. Стержень винта не только растягивается силой Р, но и закручивается моментом Т_р.

Самоторможение и к. п. д. винтовой пары. Условие самотор­можения можно записать в виде Г_отв>0, где Т_ОТВ определяется по формуле (1.8). Рассматривая самоторможение только в резь­бе без учета трения на торце гайки, получим tg(<p — \|/)>0 или

1|/«р. (1-9)

Для крепежных резьб значение угла подъема \|/ лежит в пределах 2°30'...3°30', а угол трения <р изменяется в зави­симости от коэффициента трения в пределах от 6° (при /«0,1) до 16° (при /«0,3). Таким образом, все крепежные резьбы — самотормозящие. Ходовые резьбы выполняют как самотор- мозящими, так и несамотормозящими.

Приведенные выше значения коэффициента трения, свидете­льствующие о значительных запасах самоторможения, справед­ливы только при статических нагрузках. При переменных нагрузках и особенно при вибрациях вследствие взаимных микросмещений поверхностей трения (например, в результате радиальных упругих деформаций гайки и стержня винта) коэффициент трения существенно снижается (до 0,02 и ниже). Условие самоторможения нарушается. Происходит самоотвин- чивание.

К. п. д. винтовой пары г) представляет интерес главным образом для винтовых механизмов. Его можно вычислить по отношению работы, затраченной на завинчивание гайки без учета трения, к той же работе с учетом трения. Работа завинчивания равна произведению момента завинчивания на угол поворота гайки. Так как углы поворота равны и в том и в другом случае, то отношение работ равно отношению моментов г;_ав/г_зав, в котором Г_зав определяется по формуле (1.6), а г;_ав — по той же формуле, но при /=0 и <р = 0:

Л = Пав/ Т_зяв = ^1 [(А:р/ё)/+ 1е(\]/ + ф)]. (1.10)

Учитывая потери только в резьбе (Г_т=0), найдем к. п. д. собственно винтовой пары:

Т1=^\|/Д§(\|/ + ф). (1.11)

В самотормозящей паре, где \|/ < ф, г|<0,5. Так как большинство винтовых механизмов самотормозящие, то их к. п. д. меньше 0,5.

Формула (1.11) позволяет отметить, что г| возрастает с увеличением \|/ и уменьшением ф.

Для увеличения угла подъема резьбы \|/ в винтовых механизмах применяют многозаходные винты. В практике редко используют винты, у которых ф больше 20...25°, так как дальнейший прирост к. п. д. незначителен, а изготовление резьбы затруднено. Кроме того, при большем значении \|/ становится малым выигрыш в силе или передаточное отношение винтовой пары (см. гл. 14).

Для повышения к. п. д. винтовых механизмов используют также различные средства, понижающие трение в резьбе: антифрикционные металлы, тщательную обработку и смазку трущихся поверхностей, установку подшипников под гайку или упорный торец винта, применение шариковых винтовых пар и пр.

Распределение осевой нагрузки винта по виткам резьбы. На

Т

Рис. 1.15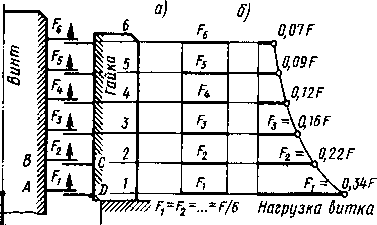

рис. 1.15 изображена схема винтовой пары. Осевая нагрузка винта передается через резьбу гайке и уравнове­шивается реакцией ее опоры. Каждый виток ре­зьбы нагружается соотве­тственно силами Г\,

..., ^2, где 2 — ЧИСЛО витков резьбы гайки.

2

Сумма = В об­

щем случае ^ не равны между собой. Задача о распределении нагрузки по виткам статически неопределима. Для ее решения уравнения равновесия дополняют уравнениями деформаций. Впервые она была решена Н. Е. Жуковским в' 1902 г. Не излагая это сравнительно сложное решение, ограничиваемся качественной оценкой причин неравномерного распределения нагрузки. В пер­вом приближении полагаем, что стержень винта и гайка абсолютно жесткие, а витки резьбы податливые. Тогда после приложения нагрузки ^ все точки стержня винга (например, А и В) сместятся одинаково относительно соответствующих точек гайки (например, С и £)). Все витки получат равные прогибы, а следовательно, и равные нагрузки (рис. 1.15, а). Во втором приближении полагаем стержень винта упругим, а гайку оставляем жесткой. Тогда относительное перемещение точек А и О будет больше относительного перемещения точек

В и С на значение растяжения стержня на участке АВ. Так как нагрузка витков пропорциональна их прогибу или от­носительному перемещению соответствующих точек, то нагруз­ка первого витка больше второго и т. д.

В действительности все элементы винтовой пары податливы, только винт растягивается, а гайка сжимается. Перемещения точки D меньше перемещений точки С на значение сжатия гайки на участке CD. Сжатие гайки дополнительно увеличит разность относительных перемещений точек А И D, В и С и т. д., а следовательно, и неравномерность нагрузки витков резьбы.

Все изложенное можно записать с помощью математических символов. Обозначим А^, Л_в, Д_с, A_D перемещения соответ­ствующих точек. Вследствие растяжения участка А В винта Д_В<Д_Л, а вследствие сжатия участка CD гайки A_D<A_C.

Относительное перемещение точек А и D, В и С

&AD — &A~ А_ВС = А_В — Ас-

Учитывая предыдущие неравенства, находим А_ЛВ>А_ВС. Следовательно, нагрузка первого витка больше нагрузки второ­го и т. д.

График распределения нагрузки по виткам, полученный на основе решения системы уравнений для стандартной шестивит- ковой гайки высотой Я=0,8*/, изображен на рис. 1.15, б. В дальнейшем решение Н. Е. Жуковского было подтверждено экспериментальными исследованиями на прозрачных моделях. График свидетельствует о значительной перегрузке нижних витков и нецелесообразности увеличения числа витков гайки, так как последние витки мало нагружены. По этому условию нецелесообразно применение мелких резьб (при высоте гайки Н=const).

Теоретические и экспериментальные исследования позволили разработать конструкции специальных гаек, выравнивающих распределение нагрузки в резьбе (рис. 1.16). На рис. 1.16, а изображена так называемая висячая гайка. Выравнивания нагрузки в резьбе здесь достигают тем, что как винт, так

Рис 1.16

и гайка растягивают­ся. При этом неравен­ство А₀<А_С изменит­ся на обратное А_В>А_С, а разность А_ло — А_вс уменьшит­ся. Кроме того, в на­иболее нагруженной нижней зоне висячая гайка тоньше и обла­дает повышенной под­атливостью, что также

способствует выравниванию нагрузки в резьбе. На рис. 1.16,6 показана разновидность висячей гайки — гайка с кольцевой выточкой. У гайки, изображенной на рис. 1.16, в, срезаны вершины нижних витков резьбы под углом 15...20°. При этом увеличивается прогиб нижних витков винта, так как они соприкасаются с гайкой не всей поверхностью, а только своими вершинами Увеличение прогиба витков снижает нагрузку этих витков.

Специальные гайки особенно желательно применять для соединений, подвергающихся действию переменных нагрузок. Разрушение таких соединений носит усталостный характер и происходит в зоне наибольшей концентрации напряжений у нижнего (наиболее нагруженного) витка резьбы. Опытом установлено, что применение специальных гаек позволяет повысить динамическую прочность резьбовых соединений на

20...30%.

Решение, результаты которого приведены на рис. 1.15, б, справедливо в пределах упругих деформаций и при номиналь­ных значениях размеров. Вследствие большой жесткости резьбы на фактическое распределение нагрузки существенно влияют технологические отклонения размеров; небольшие пластические деформации перегруженных витков, допустимые для крепежных резьб; приработка ходовых резьб. Поэтому при практических расчетах неравномерность распределения нагрузки по виткам резьбы учитывают опытным коэффициентом К_т (см. ниже).