
- •Глава 1 резьбовые соединения
- •§ 1.1. Резьба
- •§ 1.2. Основные типы крепежных деталей
- •§ 1.3. Способы стопорения резьбовых соединений
- •§ 1.4. Теория винтовой пары
- •§ 1.5. Расчет резьбы на прочность
- •§ 1.6. Расчет на прочность стержня винта (болта) при различных случаях нагружения
- •§ 1.7. Эффект эксцентричного нагружения болта
- •§ 1.8. Расчет соединений, включающих группу болтов
- •§ 1.9. Материалы резьбовых изделий и допускаемые напряжения
- •Глава 2 заклепочные соединения
- •§ 2.1. Конструкции, технология, классификация, области применения
- •§ 2.2. Расчет на прочность элементов заклепочного шва
- •§ 2.3. Материалы заклепок и допускаемые напряжения
- •Глава 3 сварные соединения
- •§ 3.1. Общие сведения и применение
- •§ 3.2. Конструкция и расчет на прочность1
- •§ 3.3. Прочность соединений и допускаемые напряжения
- •Глава 4
- •§ 4.1. Общие сведения, оценка и применение
- •§ 4.2. Соединение пайкой
- •§ 4.3. Соединение склеиванием
- •Глава 5 клеммовые соединения
- •§ 5.1. Конструкция и применение
- •§ 5.2. Расчет на прочность
- •Глава 6
- •§ 6.1. Шпоночные соединения
- •§ 6.2. Материал шпонок и допускаемые напряжения
- •§ 6.3. Оценка соединений призматическими шпонками и их применение
- •§ 6.4. Общие замечания по расчету шпоночных соединений
- •§ 6.5. Зубчатые (шлицевые) соединения
- •§ 6.6. Основные критерии работоспособности и расчета
- •§ 6.7. Расчет зубчатых соединений
- •Глава 7
- •§ 7.1. Общие сведения
- •§ 7.2. Прочность соединения
- •§ 7.3. Оценка и область применения
- •§ 7.4. Соединение посадкой на конус
- •Глава 8
- •§ 8.1. Общие сведения
- •§ 8.2. Краткие сведения о геометрии и кинематике
- •§ 8.3. Контактные напряжения и контактная прочность
- •§ 8.4. Критерии работоспособности и расчета
- •§ 8.5. Расчетная нагрузка
- •§ 8.6. Расчет прямозубых цилиндрических передач на прочность
- •§ 8.7. Особенности расчета косозубых и шевронных цилиндрических передач
- •§ 8.8. Конические зубчатые передачи
- •§ 8.9. Конические передачи с непрямыми зубьями
- •§ 8.10. Передаточное отношение одноступенчатых и многоступенчатых зубчатых передач
- •§ 8.11. Коэффициент полезного действия, охлаждение и смазка
- •§ 8.12. Материалы и термообработка
- •§ 8.13. Допускаемые напряжения
- •§ 8.14. Оптимизация конструкции зубчатых передач
- •§ 8.15. Особенности расчета планетарных передач
- •§ 8.16. Передача с зацеплением Новикова
- •§ 8.17. Краткие сведения о зубчатых передачах с перекрещивающимися осями (винтовых и гипоидных)*
- •Глава 9
- •§ 9.1. Геометрические параметры и способы изготовления передач
- •§ 9.2. Кинематические параметры передач
- •§ 9.3. Кпд червячной передачи
- •§ 9.4. Силы в зацеплении
- •§ 9.5. Оценка и применение
- •§ 9.6. Расчет прочности зубьев
- •§ 9.7. Материалы и допускаемые напряжения
- •§ 9.8. Тепловой расчет, охлаждение и смазка передачи
- •§ 9.9. Глобоидные передачи1
- •§ 10.1. Общие сведения
- •§ 10.2. Кинематические параметры и принцип действия
- •§ 10.3. Передаточное отношение и число зубьев зубчатой передачи
- •§ 10.4. Особенности преобразования движения в зубчатой передаче
- •§ 10.5. Относительное движение зубьев, выбор профиля и размеров зубьев
- •§ 10.6. Форма и размер деформирования гибкого колеса
- •§ 10.7. Рекомендации по выбору параметров зацепления и расчет гибких колес
- •§ 10.8. Кпд и критерии работоспособности передачи
- •§ 10.9. Расчет прочности гибкого колеса
- •§ 10.10. Разновидности волновых передач, их оценка и применение
- •Глава 11
- •§ 11.1. Общие сведения
- •§ 11.2. Основные типы фрикционных передач и вариаторов
- •§ 11.3. Основные факторы, определяющие качество фрикционной передачи
- •§ 11.4. Основы расчета прочности фрикционных пар
- •§ 8.3). Расчетные контактные напряжения при начальном касании по линии (тела качения — цилиндры, конусы, торы и ролики с образующими одного радиуса) определяют по формуле
- •Глава 12
- •§ 12.1. Общие сведения
- •§ 12.2. Основы расчета ременных передач
- •§ 12.3. Плоскоременная передача
- •§ 12.4. Клиноременная передача
- •§ 12.5. Передача зубчатыми ремнями
- •Глава 13
- •§ 13.1. Общие сведения
- •§ 13.2. Основные характеристики
- •§ 13.3. Конструкция основных элементов
- •§ 13.4. Силы в цепной передаче
- •§ 13.5. Кинематика и динамика цепной передачи
- •§ 13.6. Критерии работоспособности и расчета
- •§ 13.7. Практический расчет цепной передачи
- •§ 14.1. Общие сведения
- •§ 14.2. Особенности расчета резьбы винтовых механизмов
- •Глава 15 валы и оси
- •§ 15.1. Общие сведения
- •§ 15.2. Проектный расчет валов
- •§ 15.3. Проверочный расчет валов
- •4Ось вращения вапа
- •§ 16.1. Подшипники скольжения — общие сведения и классификация
- •§ 16.2. Условия работы и виды разрушения подшипников скольжения
- •§ 16.3. Трение и смазка подшипников скольжения
- •§ 16.4. Практический расчет подшипников скольжения
- •§ 16.5. Конструкции и материалы подшипников скольжения
- •§ 16.6. Подшипники качения—общие сведения и классификация
- •§ 16.7. Условия работы подшипника качения, влияющие на его работоспособность
- •§ 16.8. Практический расчет (подбор) подшипников качения
- •Глава 17 муфты
- •§ 17.1. Общие сведения, назначение и классификация
- •§ 17.2. Муфты глухие
- •§ 17.3. Муфты компенсирующие жесткие
- •§ 17.4. Муфты упругие
- •§ 17.5. Конструкция и расчет упругих муфт
- •Без загрузки (м) 21
- •§ 17.6. Муфты управляемые или сцепные
- •§ 17.7. Муфты автоматические, или самоуправляемые
- •§ 17.8. Муфты комбинированные
§ 8.6. Расчет прямозубых цилиндрических передач на прочность
Расчет на прочность прямозубых и косозубых цилиндрических передач стандартизован ГОСТ 21354—87. В курсе «Детали машин» изучают основы такого расчета. При этом вводят некоторые упрощения, мало влияющие на результаты расчетов для большинства случаев практики.
Силы в зацеплении. На рис. 8.17 Р„— нормальная сила, направленная по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. При этом силу /•’„ переносят в полюс и раскладывают на окружную Б, и радиальную Такое разложение удобно при расчете валов и опор. По заданным Т и <1 определяют
^ = 27’1/</ж1*27’1/</1 (8.5)
и через нее выражают все другие составляющие:
 ^
сс^,, Еп
/"(/соеос*,.
^
сс^,, Еп
/"(/соеос*,.
(8.6)
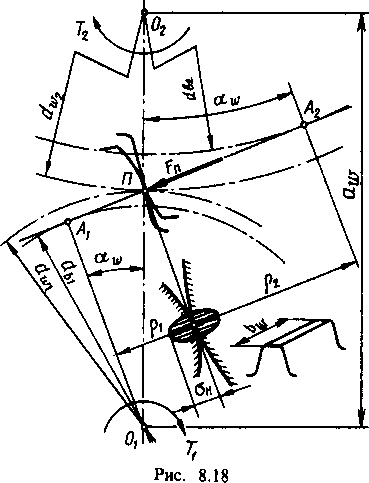
Расчет прочности зубьев по контактным напряжениям. Исследованиями установлено, что наименьшей контактной усталостью обладает околополюсная зона рабочей поверхности зубьев, где наблюдается однопарное зацепление (см. рис. 8.5). Поэтому расчет контактных напряжений принято выполнять при контакте в полюсе зацепления (рис. 8.18).
Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусами Рх и р2. При этом контактные напряжения определяют по формуле (8.2), а именно:
<ун=0,418>/^£'пр/рпр. (8.7)
Для
прямозубых передач с учетом формул
(8.4)...(8.6)
д = Р„Кн/Ь„ = Р,Кн/(Ь„со8ак)=:2Т1Кн/(с1„1Ьксо5а„). (8.8)
Радиусы кривизны эвольвент зубьев в точке контакта (рис. 8.18)
Р\. — (^япа^/г, Р 2 (^2
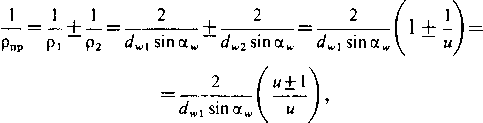 По
формуле (8.3),
По
формуле (8.3),
(8.9)
где и = (1к,2/с1к1=г2/г1, знак « + »—для наружного, а « —»—для внутреннего зацепления.
![]() Подставляя
в формулу (8.7) и заменяя сова^та*^ = (вт
2а*)/2, получаем
Подставляя
в формулу (8.7) и заменяя сова^та*^ = (вт
2а*)/2, получаем
(8.10)
Параметр и = 221г1 по ГОСТ 16532—70 называют передаточным числом и определяют как отношение большего числа зубьев к меньшему независимо от того, как передается движение: от г1 к г2 или от :2 к Это передаточное число и отличается от передаточного отношения /, которое равно отношению угловых скоростей ведущего колеса к ведомому и которое может быть мейьше или больше единицы, положительным или отрицательным. Применение и вместо / связано только с принятой формой расчетных зависимостей для контактных напряжений [см. вывод формулы (8.9), где рпр выражено через с1х (меньшее колесо), а не через с12 (большее колесо)]. Значение контактных напряжений, так же как и значение передаточного числа и, не зависит от того, какое колесо ведущее, а значение передаточного отношения / зависит. Однозначное определение и позволяет уменьшить вероятность ошибки при расчете. Передаточное число и относится только к одной паре зубчатых колес. Его не следует применять для обозначения передаточного отношения многоступенчатых редукторов, планетарных, цепных, ременных и других передач. Там справедливо только обозначение /.
Значения расчетных контактных напряжений одинаковы для шестерни и колеса. Поэтому расчет выполняют для того из колес пары, у которого меньше допускаемое напряжение [стн] — см. ниже (чаще это бывает колесо, а не шестерня).
Формулу (8.10) используют для проверочного расчета, когда все необходимые размеры и другие параметры передачи известны. При проектном расчете необходимо определить размеры передачи по заданным основным характеристикам: крутящему моменту Ту или Т2 и передаточному числу и.
С этой целью формулу (8.10) решают относительно с1х или а. Другие неизвестные параметры оценивают приближенно или выбирают по рекомендациям на основе накопленного опыта. В нашем случае принимаем ам;^а = 20о(8т2а^
% 0,6428), А^Нг«1,15 (этот коэффициент зависит от окружной скорости V, которая пока неизвестна, поэтому принято некоторое среднее значение — см.табл. 8.3). При этом из составляющих коэффициента Кн [см. формулу (8.4)] остается только Кн$. Далее обозначаем ^==6^/^—коэффициент ширины шестерни относительно диаметра.
![]() Подставляя
в формулу (8.10) и решая относительно с1и
находим
Подставляя
в формулу (8.10) и решая относительно с1и
находим
(8.11)
Решая относительно межосевого расстояния а, заменяем Т1 = Т2/и; с11=2а/(и±1) и вводим ^Ьа = Ь^/а — коэффициент ширины колеса относительно межосевого расстояния.
После преобразований с учетом зависимости
фм
= 0,5ф6в(и±1)
(8.12)
(8.13)![]()
В
приложении к ГОСТ 21354- 87 для стальных
зубчатых колес формулы (8.11) и (8.13)
записаны в виде
(8
14)
где
Кл
и Ка
- -
вспомогательные ко >ффициенты,
полученные в результате выноса числового
значения Епр
из-под знака радикала, в формулах разные
единицы одинаковых физических
величин: Г- в Н м, сі
и
а--
в мм,
ан
-в МПа.
Л‘ _ - . . _ ^ V
1 / 7![]()
![]()
Для стальных прямозубых колес А^-780 (МПа)1/3, Ка = 490 (МПа)1'3, для косозубых А^ = 680 (МПа)1'3, Ка = 430 (МПа)17 .
Вследствие этих операций не соблюдаются правила независимости расчетных формул от системы единиц физических величин. Поэтому формулы (8.14) нецелесообразно применять в учебном процессе.
Расчет значений допускаемого напряжения [ая] см. в § 8.13. Значение Кщ оценивают по рис. 8.15 в соответствии с заданной (или выбранной) схемой передачи и значением \|/м, которое рассчитывают по формуле (8.12), где значение \|/Ьа заранее выбирают по рекомендациям табл. 8.4. При выборе учитывают следующее. Увеличение \|/Ьа или относительной ширины колес позволяет уменьшить габариты и массу передачи, но вместе с этим требует повышенной жесткости и точности конструкции. В противном случае возрастает неравномерность распределения нагрузки по ширине зубчатого венца. Может оказаться, что положительное влияние увеличения ширины колес не компенсирует вредного влияния увеличения неравномерности нагрузки. Влияние различных факторов на неравномерность нагрузки рассмотрено в § 8.5.
Таблица
8.4
Редукторы
при расположении колес относительно
опор (см. рис 8 13)
Рекомендуемые
значения
Твердость
рабочих
поверхностей
зубьев
#2^350
НВ или Я, и #2
<350 НВ
Нх
и #2
>350 НВ
Симметричное
к
0,3...0,5
0,25...0,3
ФытЯ1
1,2...1,6
0,9...1,0
Несимметричное
■
тех
«Ьа
0,25...0,4
0,2...0,25
V,,
1,0...1,25
0,65...0,8
Консольное
1
тах
'Ььа
0,2...0,25
0,15...0,2
0,6...0,7
0,45...0,55
Примечания.
1. Для шевронных колес при Ь„,
равной сумме полушевронов, \1^
увеличивают в 1,3 1,4 раза 2. Для подвижных
колес коробок скоростей \|/Ьв
= 0,1...0,2. 3 Большие значения — для
постоянных и близких к ним нагрузок 4
Для многоступенчатых редукторов, в
которых нагрузка увеличивается от
ступени к ступени, в каждой последующей
ступени значения \|/Ьв,
принимают больше на 20 . 30%, чем в
предыдущей. Это способствует хорошему
отношению размеров колес по ступеням
(см § 8.9). Если при расчете выбирают
\|/Ьв,
то расчетное значение Ь„
проверяют по максимально допускаемому
значению *|/Мтах
Расчетное значение а для нестандартных редукторов округляют по ряду: /?а40: ...80; 85; 90; 95; 100; 105; 110; 120; 125; 130, далее через 10 до 260 и через 20 до 420...
Для стандартных редукторов общего применения, изготовляемых специализированными заводами, большое значение имеет ограничение числа типоразмеров корпусных деталей, когда в одном корпусе можно изготовить несколько редукторов с различными характеристиками. С этой целью по ГОСТ 2185 — 66 установлены основные параметры таких редукторов:
Стандартные межосевые расстояния а„.
й ряд—40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400, ...
й ряд- 140, 180, 225, 280, 355, 450, ...
Стандартные значения \|/Ьа: 0,1; 0,125; 0,16; 0,2; 0,25; 0,315, 0,4; 0,5, 0,63; 0,8; 1,0; 1,25.
Стандартные номинальные передаточные числа и.
й ряд—1,0; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3, 8,0
й ряд—1,12; 1,4, 1,8; 2,24; 2,8; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2
Допускаемое отклонение ±4%.
Выбор модуля и числа зубьев. В формуле (8.10) модуль и число зубьев непосредственно не участвуют. Они входят в эту формулу косвенно через с1и который определяется произведением т2х. Из этого следует, что значение контактных напряжений он не зависит от модуля или числа зубьев в отдельности, а определяется только их произведением или диаметрами колес. По условиям контактной прочности при данном с11 модуль передачи может быть сколь угодно малым, лишь бы соблюдалось равенство т21=с11.
Минимально допускаемое значение модуля можно определить из условий прочности зубьев на изгиб по формуле (8.20). Однако при таком расчете в большинстве случаев получают зацепления с очень мелкими зубьями, применение которых практически ограничено. Поэтому значение т обычно выбирают, ориентируясь на рекомендации, выработанные практикой, и затем проверяют на изгиб. В этих рекомендациях учитывают следующее.
Мелко модульные колеса с большим числом зубьев предпочтительны по условиям плавности хода передачи (увеличивается еа) и экономичности. При малых т уменьшаются потери на трение (уменьшается скольжение), сокращается расход материала (уменьшается наружный диаметр с1а = с1+2к*ат) и экономится станочное время нарезания зубьев (уменьшается объем срезаемого материала).
Крупномодульные колеса с большим объемом зубьев дольше противостоят износу, могут работать длительное время после начала выкрашивания, менее чувствительны к перегрузкам и неоднородности материала (дефекты литья и т. п.). При мелком модуле возрастают требования к точности и жесткости передачи, так как увеличивается возможность поломки зубьев вследствие концентрации нагрузки, в особенности при перегрузках. При ориентировочной оценке значения т можно использовать рекомендации табл. 8.5.
Таблица
8.5
Конструкция
'\іт
= Ь„/т, не
более
Высоконагруженные
точные передачи, валы, опоры и корпуса
повышенной жесткости:
Я
^350 НВ
45...30
Я
>350 НВ
30...20
Обычные
передачи редукторного
типа
в отдельном корпусе с достаточно
жесткими валами и опорами (и другие
аналогичные): Я^350 НВ
30
.20
Продолжение табл. 8.5
Конструкция
VI/,п
= К
/ш, не более
Н
>350 НВ
20...15
Грубые
передачи, например с опорами на
стальных конструкциях (крановые
и т. п.) или с плохо обработанными
колесами (литые), а также открытые
передачи, передачи с консольными
валами (конические), подвижные колеса
коробок скоростей
15...10
Примечание.
Меньшие значения фт
— для повторно-кратковременных режимов
работы,
значительных перегрузок и средних
скоростей; большие значения фт
- для
длительных режимов работы, небольших
перегрузок и высоких скоростей.
Выбрав по этой таблице х|/т, определяют
т = Ь„№„, (8.15)
где
Ьк = ^ы^=^Ьаа. (8.16)
Значение т согласуют со стандартом (см. табл. 8.1). Для силовых передач обычно рекомендуют принимать 1,0 мм.
При известном модуле определяют и уточняют все остальные параметры передачи.
Для передач без смещения и при хЕ = 0
</1 = 2а/(ы+1); г1=с(11т; г2 = 21Щ с12=тг2, а = 0,5 (с12±с11). (8.17)
Должно быть 21>гт1п, где гт!п — по табл. 8.6.
Для уменьшения шума в быстроходных передачах рекомендуют брать гх>25. Для окончательного утверждения выбранного значения модуля необходимо проверить прочность по напряжениям изгиба по формуле (8.19).
В случае неудовлетворительного результата изменяют т и определяют новые значения г.
При проверке можно получить аГ значительно меньше [аг ], что не является противоречивым или недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб. Если расчетное значение сгг превышает допускаемое, то применяют колеса, нарезанные с положительным смещением инструмента, или увеличивают т. Это значит, что в данной передаче (при данных материалах) решающее значение имеет не контактная прочность, а прочность на изгиб. На практике такие случаи встречаются у колес с высокотвердыми зубьями при Н> 50...60 НЁ.С (например, цементированные зубья).
Расчет прочности зубьев по напряжениям изгиба. Зуб имеет сложное напряженное состояние (см. рис. 8.10). Наибольшие напряжения изгиба образуются у корня зуба в зоне перехода эвольвенты в галтель. Здесь же наблюдается концентрация напряжений. Для того чтобы по возможности просто получить основные расчетные зависимости и уяснить влияние основных
параметров на прочность зубьев, рассмотрим вначале приближенный расчет, а затем введем поправки в виде соответствующих коэффициентов. Допустим следующее (рис. 8.19):
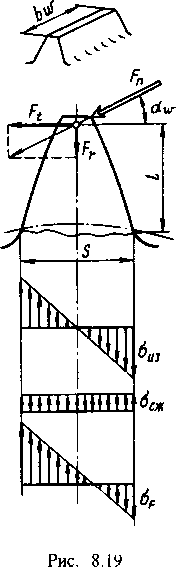 Нагрузка
в зацеплении передается одной парой
зубьев и приложена к вершине зуба.
Практика подтверждает, что этот худший
случай справедлив для 7-й, 8-й и более
низких степеней точности, ошибки
изготовления которых не могут
гарантировать наличие двухпарного
зацепления. Например (см. рис. 8.16),
ошибки шага приводят к тому, что
зубья начинают зацепляться вершинами
еще до выхода на линию зацепления. При
этом вместо теоретического двухпарного
зацепления будет однопарное.
Нагрузка
в зацеплении передается одной парой
зубьев и приложена к вершине зуба.
Практика подтверждает, что этот худший
случай справедлив для 7-й, 8-й и более
низких степеней точности, ошибки
изготовления которых не могут
гарантировать наличие двухпарного
зацепления. Например (см. рис. 8.16),
ошибки шага приводят к тому, что
зубья начинают зацепляться вершинами
еще до выхода на линию зацепления. При
этом вместо теоретического двухпарного
зацепления будет однопарное.Зуб рассматриваем как консольную балку, для которой справедливы гипотеза плоских сечений или методы сопротивления материалов. Фактически зуб подобен выступу, у которого размеры поперечного сечения соизмеримы с размерами высоты.
Точный расчет напряжений в таких элементах выполняют методами теории упругости [35]. Результаты точного расчета используют для исправления приближенного расчета путем введения теоретического коэффициента концентрации напряжений (см. ниже).
Силу Рп переносим по линии действия на ось симметрии зуба и раскладываем на составляющие и Рг. При этом радиус приложения окружной силы будет несколько больше радиуса начальной окружности. Пренебрегая этой разностью, для расчета сил ^ и Рг сохраняем формулы (8.5) и (8.6). Напряжение в опасном сечении, расположенном вблизи хорды основной окружности,
где 1¥=Ь„82/6 — момент сопротивления сечения при изгибе; А — Ьпб — площадь; Ь.», я и / указаны на рис. 8.19.
Знак «—» в формуле указывает, что за расчетные напряжения принимают напряжения на растянутой стороне зуба, так как в большинстве случаев практики именно здесь возникают трещины усталостного разрушения (для стали растяжение опаснее сжатия).
Значения / и д неудобны для расчетов. Используя геометрическое подобие зубьев различного модуля, эти величины выражают через безразмерные коэффициенты:
Г = 1/т и ^' = 5/т,
где т — модуль зубьев.
После подстановки и введения расчетных коэффициентов получают
аР
где Кр—коэффициент расчетной нагрузки (см. § 8.5); КТ теоретический коэффициент концентрации напряжений. Далее обозначают
<818>
коэффициент формы зуба (для наружных зубьев; рис. 8.20).
-М
-0.5
10 12 /4 16 20 25 30 40 50 60 80 100 150 200
Рис.
8.20
г
или 1\г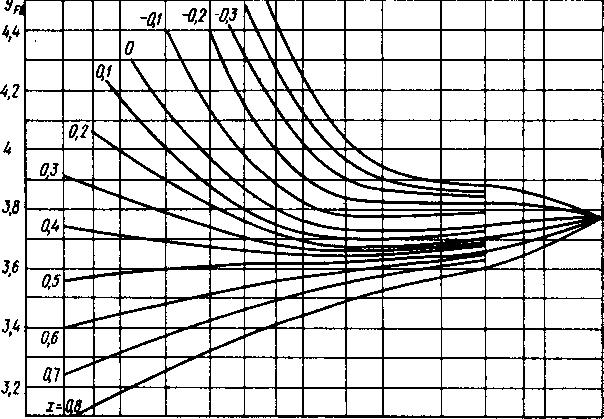
Для колес с внутренними зубьями приближенно можно принимать 1^5 = 3,5...4, большие значения — при меньших 2.
При этом для прямозубых передач расчетную формулу записывают в виде
(8>9)
где [стр ] — допускаемое напряжение изгиба (см. § 8.13).
Для проектных расчетов по напряжениям изгиба формулу (8.19) решают относительно модуля путем замены bw = tymm, Ft = 2T1/dl, dx —zxm, тогда
aF = 2 7\ KF Yfs/(z j v|/m т3).
И далее, принимая приближенно А>„= 1,5 (см. табл. 8.3), получают
m^TtKppYn/iz,^ [а,])- (8.20)
Значениями zt и v|/m задаются согласно рекомендациям табл. 8.5.
Из формулы (8.18) следует, что Yfs — безразмерный коэффициент, значения которого зависят только от формы зуба (размеры /', s', ctw) и в том числе от формы его галтели (коэффициент КТ). Форма зуба при одинаковом исходном контуре инструмента зависит от числа зубьев колеса z и коэффициента смещения инструмента х. Рассмотрим эту зависимость.
Влияние числа зубьев на форму и прочность зубьев. На
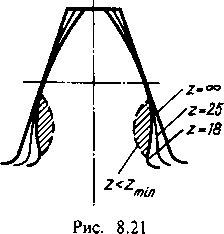 рис.
8.21 показано изменение формы зуба в
зависимости от числа зубьев колес,
нарезанных без смещения с постоянным
модулем. При z->c\j
колесо
превращается в рейку и зуб приобретает
прямолинейные очертания. С
уменьшением
z
уменьшается
толщина зуба у основания и вершины, а
также увеличивается кривизна эволь-
вентного профиля. Такое изменение формы
приводит к уменьшению прочности
зуба. При дальнейшем уменьшении z
появляется
подрезание ножки зуба (штриховая линия
на рис. 8.21), прочность зуба существенно
снижается. При нарезании инструментом
реечного типа для
прямозубых передач число зубьев на
границе подрезания
zmin
= 17.
рис.
8.21 показано изменение формы зуба в
зависимости от числа зубьев колес,
нарезанных без смещения с постоянным
модулем. При z->c\j
колесо
превращается в рейку и зуб приобретает
прямолинейные очертания. С
уменьшением
z
уменьшается
толщина зуба у основания и вершины, а
также увеличивается кривизна эволь-
вентного профиля. Такое изменение формы
приводит к уменьшению прочности
зуба. При дальнейшем уменьшении z
появляется
подрезание ножки зуба (штриховая линия
на рис. 8.21), прочность зуба существенно
снижается. При нарезании инструментом
реечного типа для
прямозубых передач число зубьев на
границе подрезания
zmin
= 17.
Функциональная зависимость коэффициента формы зуба Yfs от числа зубьев z хорошо просматривается по кривой х = 0 на рис. 8.20. Yrs интенсивно уменьшается до zv40 и далее остается примерно постоянным.
Рассмотренное влияние числа зубьев на прочность справедливо при постоянном модуле, когда с увеличением z увеличиваются и диаметры колес. При постоянных диаметрах с изменением z изменяется модуль т. В этом случае изменяются не только форма, но и размеры зуба. С увеличением z форма улучшается, а размеры уменьшаются (уменьшается т). Уменьшение модуля снижает прочность зуба на изгиб [см. формулу (8.19)].
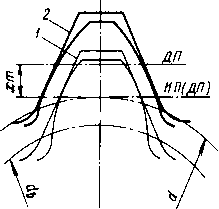
Смещение инструмента при нарезании зубьев и его влияние на форму и прочность зубьев. На рис. 8.22 изображено два положения инструмента (рейки) при нарезании зубьев: 1 —
делительная плоскость рейки (ДП) совпадает с начальной плоскостью (НП) — нарезание без смещения; 2—инструменту дано положительное смещение хт. При этом основной с1ь и делительный с/ диаметры колеса не изменяются, так как не изменяется г (НП по-прежнему обкатывается по с1, а ДП смещена на хт). Как видно из чертежа, смещение инструмента вызвало значительное изменение формы зуба. Толщина зуба у основания увеличилась, увеличилась и прочность зуба по напряжениям изгиба. Одновременно с этим заострилась головка зуба. Заострение является одной из причин, ограничивающих значение смещения инструмента. Отрицательное смещение инструмента сопровождается явлениями обратного характера.
 Применяют
два типа передач со смещением:
Применяют
два типа передач со смещением:
Шестерню изготовляют с положительным смещением (х!>0), колесо — с отрицательным (лг2<0), но так, что | лг11 = | лг2 I или х1 = л:1+д:2 = 0.
При любом смещении сумма ширины впадины и толщины зуба по делительной окружности равна шагу р. Одинаковые по значению, но разные по знаку смещения вызывают одинаковые увеличения толщины зуба шестерни и ширины впадины колеса. Поэтому в зацеплении зубчатой пары при лгх = 0 делительные окружности соприкасаются и являются начальными, как в передаче без смещения. Не изменяются также межосевое расстояние а„ и угол зацепления ак:
а„ = а = 0,5(с11+с12); аи, = а = 20°.
Изменяется только соотношение высот головок и ножек зубьев.
Суммарное смещение хъ не равно нулю. Обычно х£>0, а также хх>0 и х2>0. При положительных х1 и х2 делительная толщина зубьев шестерен и колеса больш р!2. Поэтому делительные окружности не могут соприкасаться. Начальными становятся новые окружности, большие, чем делительные (й^н,!>^, <Лк2>й2', см. рис. 8.4). Межосевое расстояние увеличивается:
йу! = 0,5 (^ 1 ■+■ (1^2) > а = 0,5 (<^ ■+■ (12 )•
При этом увеличивается и угол наклона линии зацепления как общей касательной к основным окружностям, т. е. увеличивается угол зацепления: аи,>а = 20°. Увеличение
аи, сопровождается уменьшением коэффициента перекрытия еа, что является отрицательным и служит одной из причин, ограничивающих применение больших смещений.
Нарезание со смещением позволяет во многих случаях повысить качество зубчатого зацепления. Применяя смещение, необходимо помнить:
Положительное смещение повышает прочность зубьев на изгиб и устраняет подрезание при малом числе зубьев (понижает гт1п). Например (см. рис. 8.20), при 2 = 25 увеличение х от нуля до +0,8 уменьшает в 1,2 раза. Соответственно уменьшаются и напряжения изгиба [см. формулу (8.19)]. В соответствии с габл. 8.6 можно понизить 2т!п от 17 до 8.
Увеличение аи, при хЕ>0 повышает контактную прочность [см. формулу (8.10)]. Можно увеличить <х„ до 25° и поднять допускаемую нагрузку приблизительно на 20%.
При большом числе зубьев у шестерни и колеса смещение малоэффективно, так как форма зуба даже при значительных смещениях почти не изменяется. (У зубчатой рейки, которая подобна колесу при 2 = со, смещение совершенно не изменяет форму зуба.)
Передачи со смещением при хх = 0 применяют при больших и и малых г1. В этих условиях смещения лг^О и дг2<0 выравнивают форму зубьев шестерни и колеса и приближают их к равнопрочноети по изгибу.
Смещения при хХт^0 могут влиять на большее число параметров зацепления. Рекомендации по выбору коэффициентов смещения даны в ГОСТ 16532—70. Некоторые из этих
рекомендаций
приведены
в
табл. 8.6.
Таблица
8.6
Коэффициент
смещения
Передачи
шестерни
Хг
колеса
*2
прямозубые
косозубые
и шевронные
0
0
Zi
^21
М
^ ^гпт 2
0,3
-0,3
14^z!
<20
и м^3,5
21^*!шп
+ 2, но не
менее 10 и 3,5. Рекомендация не
распространяется на передачи, у
которых при твердости колеса <320
НВ твердость шестерни превышает не
более чем на 70 НВ
0,5
0,5
10
<zt<
<30
* (Граничение по подрезанию ß,
град
до 12 св 12 до 17 св 17 до 21 св 21 до 24 св 24 до 28
17 16 15 14 13
