3.1.4 Преобразование структуры типа «треугольник» в структуру типа «звезда».

Сущность этого приема поясняется с помощью рис.3.6. Исходя из основного критерия эквивалентного преоб­разования равенства ПН цепей «треугольника» и «звезды» между одинаковыми точками и учитывая правила перехода от ФАЛ к ВФ (3.4) - (3.6), можно для структуры, показанной на рис.3.6, составить систему уравнений:

(3.7)

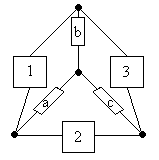
Рис.3.6

В результате решения системы уравнений (3.7) определяются значения ПН элементов эквивалентной «звезды» . В частном случае, когда все элементы равнонадежны:

.

Если в исходной НФС может быть выделено несколько звеньев типа «треугольник», преобразование делают одновременно для всех звеньев, как это показано на рис.3.6.

Для упрощения расчетов значений и без существенной потери точности рекомендуется следующий прием. В системе уравнений (3.7) ПН р записываются через вероятности отказов . Если в полученной новой системе уравнений пренебречь произведениями вида , , и , то получим соотношения:

; ; (3.8)

Еще раз обратившись к рис.3.6, определим простое правило составления уравнений (3.8): выражение запи­сывается обязательно для вероятностей отказа, причем этот показатель для элемента «звезды», присоединяемого к какой-либо вершине «треугольника», равен произведению показателей элементов «треугольника», прилегающих к этой же вершине. Для дальнейших расчетов делается об­ратный перевод показателей в показатели , например,

.

3.1.5 Алгоритм разрезания

Этот прием преобразования отличается от предыдущего универсальностью, то есть он может быть использован для любых типов структур. Однако он отли­чается большей трудоемкостью процедур, что определяет условие целесообразности его применения в тех случаях, когда преобразование «треугольник» — «звезда» не подхо­дит. Метод основан на использовании формулы полной вероятности. Сущность приема заключается в следующем.

В исходной НФС выбирают так называемый ключе­вой элемент с наибольшим числом связей с другими элементами структуры. После этого из исходной НФС получают две производные структуры: в первой этот элемент идеально надежен, во второй он всегда нера­ботоспособен (отсутствует). Производные структуры могут быть представлены в виде схем или алгебраических выражений. При геометрической интерпретации в первой схеме вместо ключевого элемента ставится перемычка, во второй - делается разрыв. При алгебраической записи производных НФС их представляют в виде двух ФАЛ. Первую получают подстановкой в исходную ФАЛ вместо логической переменной ключевого элемента логическую единицу, вторую - подстановкой логического нуля. Первая производная ФАЛ умножается на истинное значение логической переменной ключевого элемента, вторая - на ее ложное значение (инверсию), после чего они ариф­метически суммируются. Если после первого шага разрезания производная НФС не превратится в параллельно-последовательную структуру, в каждой из них независимо друг от друга выбирают по указанному критерию следующий ключевой элемент и так до тех пор, пока преобразуемые структуры не примут параллельно-последовательный вид.

Обращаем внимание на то, что в отличие от метода «треугольник – звезда» разложение по ключевым элементам должно выполняться итеративно. Одновре­менный выбор сразу нескольких ключевых элементов недопустим.

Если необходимо выбрать несколько ключевых эле­ментов, то алгебраическая форма разложения более целесообразна, так как уменьшает трудоемкость проце­дуры преобразований. Поэтому рассмотрим пример прим­енения алгоритма разрезания с использованием алгебра­ической записи производной ФАЛ.

Пример 3. Определить вероятность безотказной работы невосстанавливаемой системы, НФС которой изображена на рис.3.5.

Решение: ФАЛ, записанная через СДНФ по формуле (3.2), будет иметь вид

.

Эта ФАЛ не является бесповторной. В ней элементами с наибольшим числом связей являются и . Выбираем в качестве ключевого элемент . Тогда в соответствии с указанными выше правилами можно записать:

.

Первая производная ФАЛ еще не стала беспо­вторной, вторая — бесповторная. Следует учитывать, что эти ФАЛ между собой независимы, поэтому наличие в них некоторых одинаковых логических переменных не имеет значения. Выбираем на втором шаге итерации в первой ФАЛ в качестве следующего ключевого элемента как наиболее часто повторяющийся. Получим функцию следу­ющего вида:

.

На третьем шаге в выражении при в качестве ключевого формально может быть выбран любой из повто­ряющихся элементов, поскольку они встречаются одинаково часто, но целесообразно выбрать так как его исключение уберет диагональную связь и, следовательно, быстрее приведет структуру к параллельно-последова­тельному виду.

.

Обращаем внимание на то, что выражение при было приведено к бесповторной форме способом скле­ивания вместо выбора очередного ключевого элемента, что, безусловно, менее трудоемко. Поэтому всегда надо иметь в виду, что перед выбором или в ходе выбора ключевых элементов целесообразно пробовать применять минимизацию булевых выражений путем склеивания. Это во многих случаях позволяет уменьшить число итераций преобразования.

Полученное для выражение переводим по формулам (3.4)-(3.6) в вероятностную функцию:

.

Для расчетов с помощью ЛВМ средней наработки до отказа необходимо пользоваться формулой:

предварительно составив ВФ для функции ВБР невосстанавливаемой системы через функции ВБР ее элементов при известном законе распре­деления времени их работы до отказа.

Пример. Пусть ВФ имеет вид .

Требуется определить системы, если время безотказной работы элементов подчиняется экспоненци­альному распределению, а .

Решение:

; ;

.

Аналогичный подход с использованием общей расчетной формулы:

.

должен быть использован, если необходимо оценить интенсивность отказов систем.

3.2 ЛАБОРАТОРНАЯ РАБОТА 5

ТЕМА: Расчёт надёжности сложноструктурных систем методом свёртки структуры системы (ССС).

Предлагается метод оценивания характеристик структурно- сложных систем, обеспечивающий возможность поиска их оптимальных структур в рамках статистического моделирования благодаря высокому быстродействию вычислительного алгоритма. Оценки находят путём свёртки структуры системы (ССС) на основе правил преобразования специальной матрицы связей.

Решение задач структурного синтеза систем зачастую сталкивается с проблемой исследования их поведения в диапазоне реальных условий применения, проявляющихся стохастически. Такое исследование наиболее удобно проводить в рамках статистического моделирования. Но алгоритмы расчета характеристик системы, построенные на основе известных логико-вероятностных методов, требуют больших вычислительных затрат даже при однократном расчете, а статистическое моделирование, как правило, предполагает расчет характеристик системы в каждой реализации. Поэтому, чтобы сделать возможным анализ последствий реконфигурации системы в рамках статистической модели, нужны алгоритмы с очень высоким быстродействием. Для достижения этой цели необходимо в первую очередь исключить полную запись функций характеристик системы через характеристики ее элементов, связанную с основными вычислительными затратами в известных методах. Эта проблема в существенной степени преодолевается путем ССС на основе преобразования матрицы связей. Принципиальное отличие такого метода от известных состоит в том, что полная запись функций характеристик системы не проводится, а характеристики системы рассчитываются в ходе выполнения вычислительного алгоритма.

При использовании этого метода структура системы представляется графом G(H,V), где H-множество вершин, характеризующих соединения элементов; V- множество дуг, характеризующих элементы. Каждый элемент называется связью. Тогда матрица связей состоит из N строк и N столбцов (N- число вершин). Элементы в для i-й строки (i= ) и j-го столбца (j= ) обозначаются s(i,j) и определяются следующим образом:

s(i,j) =

Для задания двухполюсного графа устанавливаются номера входной Kвх и Kвых вершин. Параметры элементов задаются матрицами и . Элементы t(i,j) матрицы времен содержат характеристики быстродействия элементов системы, а элементы p(i,j) матрицы - характеристики их надежности. С учетом возможных элементарных параллельных связей в исходной структуре системы предусматривается трехмерное задание и . Тогда их элементы выражаются соответственно t(i,j) и p(i,j) [ где q-номер связи вершины i с вершиной j в дуге v(i, j) , q= ], а дуга v(i, j) определяется как множество параллельных по отношению друг к другу элементарных связей вершины i с вершиной j. Если Q=1, то p(i,j) обозначается p(i,j), t(i,j) - t(i, j), а дуга v(i, j) называется одинарной и характеризует одну связь.

Свертка структуры системы основывается на применении правил идентификации элементарных подграфов, правил расчета параметров их эквивалентов и правил преобразования значений элементов матриц , и .

Правило 1. В k-ой строке идентифицируется “висящая” вершина, связанная с m-й вершиной, если

А :

Тогда в осуществляется преобразование .

Правило 2. В k-ой строке идентифицируется “петля” если

А : то в выполняется преобразование s(k,k)=0.

Правило 3. В идентифицируются параллельные связи если:

А : , в характеристика надежности определяется как , а в проводится преобразование .

Правило 4. В k-й строке одинарные дуги l) и (k,m) идентифицируются как последовательные; если

А : , тогда в рассчитывается характеристика надежности: p(l,m) = p(m,l) = p(k,l) p(k,m).

В текущие значения элементов s преобразуются к значениям s

Правило 5. Если для двух одинарных дуг и в k-й строке :

А , то это означает, что одинарные дуги , и образуют схему “треугольник”. Тогда осуществляется преобразование “треугольник” - “звезда” и рассчитываются характеристики надежности относительно дополнительной вершины с номером N+1:

где

Матрица дополняется строкой и столбцом, а значения элементов изменяются:

Содержание алгоритма ССС состоит в последовательном цикличном применении этих правил. Каждый шаг алгоритма предполагает реализацию последовательности проверок выполнения условий (А ….,А ) во всех строках матрицы . Переход к проверке следующего условия определяется неудовлетворением предыдущего. При выполнении любого из условий проводятся соответствующие преобразования в , и , и алгоритм начинает следующий шаг с проверки А .

Особенностью алгоритма является то, что в процессе его реализации не создается более двух параллельных связей. Их большее число возможно только в исходной структурной схеме . В результате преобразований, связанных с выполнением условия А , текущее значение N увеличивается на 1.

Искомая оценка быстродействия рассчитывается путем сопровождения изменений значений матрицы .

При задании искомого параметра быстродействия в осуществляются предварительные преобразования. Для отыскания минимальной продолжительности

, а максимальной .

Если по правилам 1 и 4 в обнуляются k-е строка и столбец, то в матрице текущие значения t зафиксированные перед этим шагом алгоритма, преобразуются к новым значениям t Преобразования для оценивания минимального времени осуществляются последовательным выполнением следующих действий.

Действие 1.

Действие 2.

Завершение расчетов определяется таким состоянием матрицы , при котором в ней остается только один значимый элемент, соответствующий параметру быстродействия системы между входной и выходной вершинами.

Максимальная и бесповторная (элемент системы задействуется только один раз) продолжительность оценивается по выражению, аналогичному для действия 1, но вместо min используется max.

Применение алгоритма по методу ССС на основе преобразования матрицы связей практически ограниченно планарными графами. Обеспечивается решение задачи для полных графов не более чем с четырьмя вершинами. Для преодоления этих ограничений и снижения вычислительных затрат при моделировании целесообразно использовать комбинацию алгоритмов по методу свертки и логико-вероятностному методу в виде двухэтапной процедуры. На первом этапе структурная схема системы сворачивается по матрице связей, а результат свертки представляется матрицей переходов. На втором этапе применяется алгоритм, построенный по одному из логико-вероятностных.

Для прикладного использования предлагаемого алгоритма в процессе выбора оптимальных решений по модернизации системы предполагается учесть моделирование всех допустимых конфигураций системы, что осуществляется путем внесения соответствующих изменений в матрицу связей, вызванных реконфигурацией системы, и добавления данных о характеристиках новых элементов. Высокое быстродействие алгоритма обеспечивает возможность полного перебора вариантов и оценивание их с позиций надежности и быстродействия системы. Тем самым находится оптимальное решение.

Пример решения задачи.

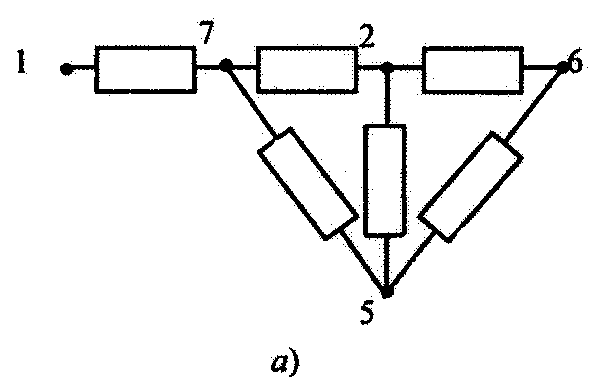
Рассмотрим пример использования алгоритма для расчета оценок надежности и быстродействие системы, структурная схема которой представлена на рис. 3.7, а. Проиллюстрируем преобразования структурной схемой, матрицей связей и матрицей времен, при , не останавливаясь на расчете характеристик надежности эквивалентов из-за его тривиальности. При этом характеристики быстродействия элементов системы задаются в следующим образом:

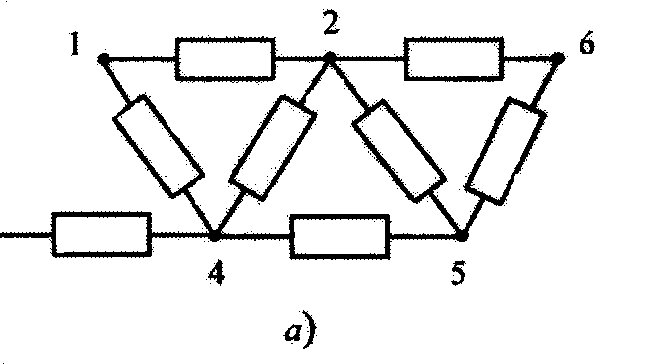
Остальные значения элементов в - нулевые:

i	j
	1	2	3	4	5	6
1	0		0		0	0
2		0	0
3	0	0	0		0	0
4				0		0
5	0		0		0
6	0		0	0		0

i	j
	1	2	3	4	5	6
1	0	1	0	1	0	0
2	1	0	0	1	1	1
3	0	0	0	1	0	0
4	1	1	1	0	1	0
5	0	1	0	1	0	1
6	0	1	0	0	1	0

б) в)

Рис. 3.7 Структурная схема системы (а), матрица связей (б) и матрица времен (в)

i	j
	1	2	3	4	5	6
1	0		0		0	0
2		0	0
3	0	0	0	0	0	0
4			0	0		0
5	0		0		0
6	0		0	0		0

i	j
	1	2	3	4	5	6
1	0	1	0	1	0	0
2	1	0	0	1	1	1
3	0	0	0	0	0	0
4	1	1	0	0	1	0
5	0	1	0	1	0	1
6	0	1	0	0	1	0

б) в)

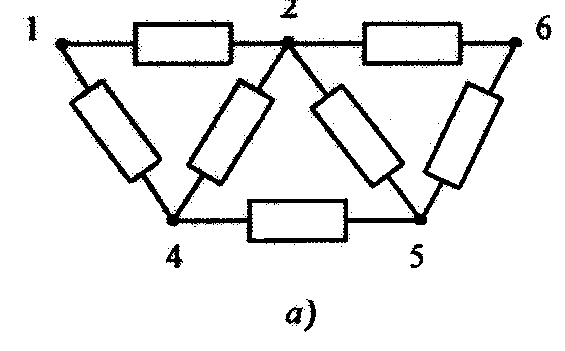
Рис. 3.8 Структурная схема системы (а), матрица связей (б) и матрица времен (в) после первого шага алгоритма

На первом шаге алгоритма устанавливается, что в третьей строке матрицы связей выполняется . Для ликвидации найденной “висящей” вершины обнуляются соответствующие строки и столбцы и . Результат преобразования виден из рис.3.8. В дальнейшем обнуленные строки и столбцы показываться не будут.

На втором шаге алгоритма устанавливается, что ,….., не выполняются, а относительно вершин 1, 2, 4 в (см. рис. 3.8,б) выполняется . Поэтому осуществляются действия согласно выражениям (5) и (6). В результате структурная схема преобразуется к форме, представленной на рис.3.9, а, а принимает вид, показанный на рис. 3.9, б. Тем самым подграф с вершинами 1, 2, 4, соответствующий схеме “треугольник”, преобразуется к схеме “звезда” с вершинами 1, 7, 2, 4. В изменений нет.

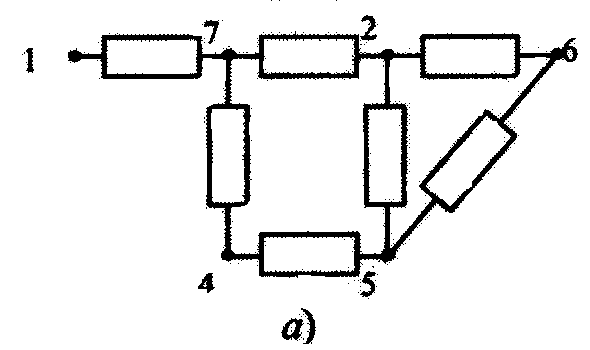
На третьем шаге алгоритма последовательная проверка ,….., . В (рис. 3.9, б) А и А не выполняются. Для вершины 4 выполняется . Поэтому осуществляются действия по формулам (3) и (4).

i	j
	1	2	3	4	5	6
1	0		0		0	0
2		0	0
3	0	0	0	0	0	0
4			0	0		0
5	0		0		0
6	0		0	0		0

i	j
	1	2	4	5	6	7
1	0	0	0	0	0	1
2	1	0	0	1	1	1
4	0	0	0	1	0	1
5	0	1	1	0	1	0
6	0	1	0	1	0	0
7	1	1	1	0	0	0

б) в)

Рис. 3.9. Структурная схема системы (а), матрица связей (б) и матрица времен (в) после второго шага алгоритма

i	j
	1	2	3	4	5	6
1	0		0		0	0
2		0	0	0
3	0	0	0	0	0	0
4	0	0	0	0	0	0
5			0	0	0
6	0		0	0		0

i	j
	1	2	3	4	5	6
1	0	1	0	1	0	0
2	1	0	0	1	1	1
3	0	0	0	0	0	0
4	1	1	0	0	1	0
5	0	1	0	1	0	1
6	0	1	0	0	1	0

б) в)

Рис. 3.10. Структурная схема системы (а), матрица связей (б) и матрица времен (в) после третьего шага алгоритма

Структурная схема системы и принимают вид, представленный на рис. 3.10. В связи с исключением вершины 4 в проводятся преобразования t = t (1,2) = t (2,1) = min ;

t = t (1,5) = t (5,1) = t + t ;

t = t (2,5) = t (5,2) = min .

На четвертом шаге алгоритма проверка условий снова начинается с . В (см. рис. 3.10, б)

,….., не выполняются. Для вершин 2, 5, 6 выполняется . Поэтому проводятся расчеты и преобразования по выражениям (5) и (6). Значения в не изменяются. Результаты преобразований даны на рис. 3.11.

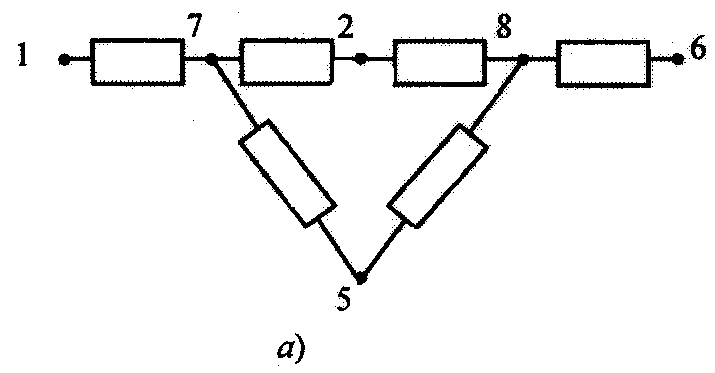
На пятом шаге алгоритма выполняется для вершины 2. Осуществляются действия (3) и (4) для , в - преобразования, связанные с исключением вершины 2:

i	j
	1	2	5	6	7	8
1	0	0	0	0	1	0
2	1	0	0	0	1	1
5	0	0	0	0	1	1
6	0	0	0	0	0	1
7	1	1	1	0	0	0
8	0	1	1	1	0	0

i	j
	1	2	3	4	5	6
1	0		0		0	0
2		0	0	0
3	0	0	0	0	0	0
4		0	0	0	0	0
5	0		0	0	0
6	0		0	0		0

б) в)

Р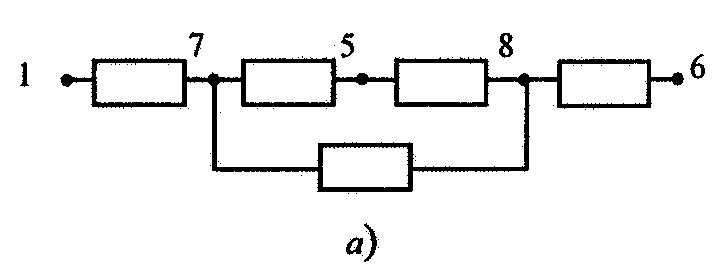 ис. 3.11. Структурная схема системы (а), матрица связей (б) и матрица времен (в) после четвертого шага алгоритма

i	j
	1	5	6	7	8
1	0	0	0	1	0
5	0	0	0	1	1
6	0	0	0	0	1
7	1	1	0	0	1
8	0	1	1	1	0

i	j
	1	2	3	4	5	6
1	0		0	0	t	t
2	0	0	0	0	0	0
3	0	0	0	0	0	0
4	0	0	0	0	0	0
5		0	0	0	0
6		0	0	0		0

б) в)

Рис. 3.12. Структурная схема системы (а), матрица связей (б) и матрица времен (в) после пятого шага алгоритма

Результат преобразований показан на рис. 3.12.

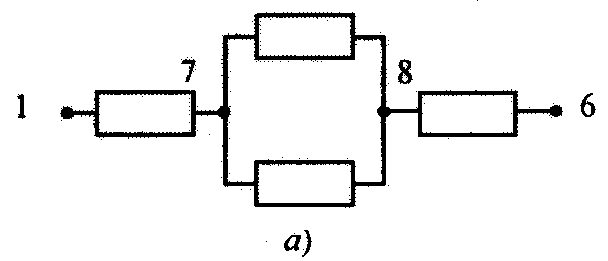
На шестом шаге аналогичные действия проводятся для вершин 5. Их результат виден из рис. 3.13. При этом в :

Найденное значение t -искомая оценка быстродействия.

Согласно (рис. 3.13,б) характеристика надежности элемента, соответствующего дуге (7,8), сохранена как после пятого шага, а элемента, эквивалентного элементам, образовавшим дуги (7,5) и (5,8) (см. рис. 3.12, а), определена как после шестого шага алгоритма. В на седьмом шаге алгоритма выполняется для вершин 7, 8 и осуществляются действия согласно (1) и (2).

i	j
	1		6	7	8
1		0	0	1	0
6		0	0	0	1
7		1	0	0	2
8		0	1	2	0

i	j
	1	2	3	4	5	6
1	0	0	0	0	0	t
2	0	0	0	0	0	0
3	0	0	0	0	0	0
4	0	0	0	0	0	0
5	0	0	0	0	0	0
6	t	0	0	0	0	0

б) в)

Рис. 3.13. Структурная схема системы (а), матрица связей (б) и матрица времен (в) после шестого шага алгоритма

i	j
	1	6	8
1	0	0	1
6	0	0	1
8	1	1	0

i	j
	1	2
1	0	1
2	1	0

i	j
	1	6	7	8
1	0	0	1	0
6	0	0	0	1
7	1	0	0	1
8	0	1	1	0

а) б) в)

Рис. 3.14. Матрица связей после седьмого (а), восьмого (б) и девятого (в) шагов алгоритма

На восьмом шаге алгоритма выполняется для вершины 7, а на девятом – для вершины 8. Содержание после седьмого, восьмого и девятого шагов алгоритма представлено на рис. 3.14.

Выполнение алгоритма прекращается, когда структурная схема системы сворачивается до одного эквивалентного элемента или когда алгоритм исчерпывает свои возможности. В нашем случае преобразования завершены после девятого шага алгоритма.

Для оценивания вычислительной эффективности алгоритма, разработанного по предложенному методу, проведено его сравнение с алгоритмами, построенными на основе известных методов. Сравнение осуществлялось путем сопоставления времени вычисления вероятности безотказной работы систем, представленных наиболее часто встречающимися структурами организационного управления. Полученные данные позволяют сделать вывод, что в реальном диапазоне сложности исследуемых структур (более 20 элементов) быстродействие разработанного алгоритма более чем в 1 млн. раз превышает быстродействие алгоритмов, построенных на основе известных методов, при этом с повышением сложности структуры исследуемой системы разница в быстродействии резко возрастает.

3.3. ЛАБОРАТОРНАЯ РАБОТА 6

ТЕМА: Обработка результатов определительных и контрольных испытаний на надёжность.