3.1.3 Логико-вероятностный метод

Теоретической основой ЛВМ является математическая логика (булева алгебра), которая оперирует с логическими выражениями, имеющими значения «истинно» (1) или «ложно» (0). Логические выражения y являются функциями логических переменных x₁, x₂, …,x_n, каждая из которых также может иметь значения 0 или 1. Из n переменных может быть образовано 2ⁿ наборов и 2²ⁿ логических функций.

Логические функции, которые применительно к задачам надежности принято называть функциями работоспособности (надежности), могут задаваться в словесной форме, таблицами истинности, алгебраическими выражениями или графиками.

Для записи функции работоспособности в алгебраической форме используется одно из следующих выражений:

(3.2)

или

(3.3)

где y_i – значение функции работоспособности для соответствующей строки, 0 или 1;

m_i – конъюнкция набора элементов i-ой строки;

M_i – дизъюнкция набора элементов i-ой строки.

Представление функции работоспособности в виде (3.2), включающем в каждую дизъюнкцию конъюнкции всех элементов, называют совершенной дизъюнктивной нормальной формой (СДНФ), а в виде (3.3) - совершенной конъюнктивной нормальной формой (СКНФ).

Для записи функции работоспособности в минимальной бесповторной дизъюнктивной форме могут быть использованы минимальные пути, а в конъюнктивной – минимальные сечения. Принципы их определения рассмотрены ранее.

В качестве примера запишем функцию алгебры логики (ФАЛ) в виде СДНФ и СКНФ, описывающих усло­вия работоспособности системы с НФС, изображенной на рис. 3.5.

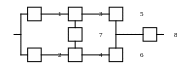
Рис.3.5

ФАЛ, записанная через СДНФ по формуле (3.2), будет иметь вид:

.

ФАЛ, записанная по формуле (3.3) имеет вид:

Раскрыв скобки во втором выражении и сделав несложные преобразования, нетрудно убедиться, что эти выражения тождественны, однако запись ФАЛ через СКНФ получилась более громоздкой. При оценке надежности невосста­навливаемых систем запись ФАЛ через СКНФ может быть рекомендована лишь в том случае, когда в НФС явно преобладают параллельные соединения элементов.

Обязательным условием выполнения расчетов ПН для невосстанавливаемых систем является получение ФАЛ в так называемой бесповторной форме.

Как видно из приведенного примера, процедуры составления исходных ФАЛ и их приведение при необ­ходимости в бесповторную форму для многокомпонен­тных систем могут оказаться весьма громоздкими и трудоемкими. Эти трудности возрастают при сетевых структурах систем, так как требуются специальные способы преобразования исходных повторных ФАЛ в бесповторные, то есть такие, в которых каждая логическая переменная присутствовала бы в прямом или инверсном виде лишь один раз. Для практического занятия достаточно изучить способ преобразования структуры типа "треугольник" в эквивалентную ей по характерис­тикам надежности структуру типа "звезда" и способ (алгоритм) разрезания (разложения исходной структуры по ключевым элементам).

Рекомендованные способы преобразования НФС примерно равноценны лишь при условии разложения по одному ключевому элементу. Если таких элементов в исходной структуре несколько, проще использовать метод преобразования "треугольник-звезда". Однако в отличие oт алгоритма разрезания он может быть применен только тогда, когда в НФС имеются замкнутые контуры типа "треугольник".

Перед тем, как рассмотреть способы получения бесповторных ФАЛ, сформулируем правила перехода от логической функции к вероятностной:

1) символ функции работоспособности в левой части ФАЛ заменяется на символ вероятностного ПН системы;

2) символы каждой логической переменной заменяются на вероятностный ПН соответствующего элемента системы, причем

, а (3.4)

3) конъюнкций из логических переменных переводится в произведение М вероятностных ПН соответствующих элементов системы

, (3.5)

4) дизъюнкция из М логических переменных переводится а выражение следующего вида:

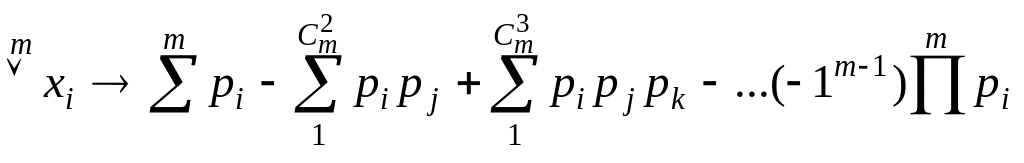, (3.6)

где ; ; ; ;

m полный набор номеров элементов НФС;

число сочетаний из M членов по N.

Перейдем к рассмотрению эквивалентных преобразований повторных ФАЛ в бесповторные.