- •Лабораторная работа №3,4
- •2.2 Лабораторная работа №5
- •2.3 Лабораторная работа №6
- •3. Порядок выполнения лабораторных работ
- •3.1 Лабораторная работа 3,4
- •3.1.1 Метод минимальных путей и сечений
- •3.1.2 Метод разложения относительно особого элемента
- •3.1.3 Логико-вероятностный метод
- •3.1.4 Преобразование структуры типа «треугольник» в структуру типа «звезда».
- •3.1.5 Алгоритм разрезания
- •3.3.1. Определительные испытания
- •3.3.2. Примеры решения задач
- •3.3.3. Контрольные испытания
- •3.3.4. Пример решения задачи
Лабораторная работа №3,4
Цель: Расчёт надёжности невосстанавливаемых сложных систем с использованием различных методов.
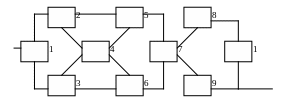
ЗАДАНИЕ. Система описывается надёжностной функциональной схемой (НФС), представленной на рисунке 1.Элементы системы характеризуются следующими показателями надёжности:
интенсивность отказов
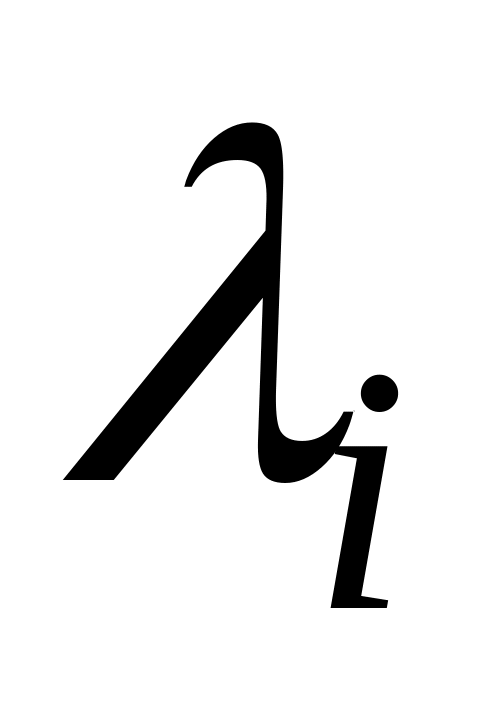 ,
ч-1;
,
ч-1;оперативное время восстановления tоп, ч.
Исходные данные по вариантам представлены в таблице 1 и на рисунке 1.
Необходимо, используя метод минимальных путей и сечений(лабораторная №3), метод разложения относительно особого элемента(лабораторная работа №4) рассчитать следующие показатели надёжности невосстанавливаемой системы:
вероятность безотказной работы
 ;
;среднюю наработку до отказа
 ;
;интенсивность отказов
 .
.
Таблица 1- Варианты заданий и исходные данные
№в. |
№сх. |
|
λ110-4, ч-1 |
λ210-4, ч-1 |
λ310-4, ч-1 |
λ410-4, ч-1 |
λ510-4, ч-1 |
λ610-4, ч-1 |
λ710-4, ч-1 |
λ810-4, ч-1 |
λ910-4, ч-1 |
λ1010-4, ч-1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
1 |
1 |
600 |
1 |
- |
4 |
1 |
1,5 |
2,5 |
2 |
4 |
4,5 |
1 |
2 |
2 |
610 |
2 |
2,5 |
3 |
- |
5 |
4 |
2,5 |
1,5 |
1 |
1 |
3 |
3 |
620 |
3 |
1 |
1 |
2,5 |
3 |
3 |
5 |
2,5 |
1- |
2,5 |
4 |
4 |
630 |
4 |
2,5 |
2.5 |
1 |
1,5 |
1,5 |
3 |
- |
2,5 |
3 |
5 |
5 |
640 |
5 |
1,5 |
2 |
3 |
1,5 |
- |
2,5 |
1 |
2 |
4 |
6 |
6 |
650 |
1,5 |
1 |
2 |
3 |
2,5 |
3 |
3 |
2,5 |
- |
1,5 |
7 |
7 |
660 |
3 |
1,5 |
2,5 |
2 |
4 |
1 |
- |
1 |
2 |
2,5 |
8 |
8 |
670 |
6 |
1 |
1,5 |
2 |
- |
1 |
4 |
2,5 |
3 |
- |
9 |
9 |
680 |
2,5 |
2 |
4 |
- |
1,5 |
2 |
5 |
3 |
1,5 |
2,5 |
10 |
10 |
690 |
4 |
1,5 |
2 |
5 |
3 |
4 |
- |
2,5 |
2 |
- |
11 |
11 |
700 |
2 |
3 |
5 |
1,5 |
1 |
1 |
5 |
2 |
2,5 |
- |
12 |
12 |
710 |
- |
1,5 |
2 |
1 |
4 |
2 |
3 |
1 |
5 |
1,5 |
13 |
13 |
720 |
3,5 |
2 |
3 |
1,5 |
2 |
1,5 |
2,5 |
3 |
1 |
- |
14 |
1 |
730 |
6,5 |
2,5 |
4 |
2 |
1,5 |
1 |
22 |
4 |
2 |
2 |
15 |
2 |
740 |
3,5 |
1 |
1,5 |
5 |
4 |
2,5 |
3 |
1 |
5 |
4 |
16 |
3 |
750 |
2 |
1,5 |
3 |
2 |
1 |
5 |
2,5 |
3,5 |
2 |
3 |
17 |
4 |
760 |
6 |
4 |
1 |
5 |
3 |
3 |
1 |
4 |
1,5 |
1 |
18 |
5 |
770 |
4 |
1,5 |
2 |
3 |
1 |
2 |
1,5 |
3 |
2,5 |
2 |
19 |
6 |
780 |
3,5 |
4 |
1,5 |
1 |
2,5 |
4 |
1.5 |
1 |
2,5 |
3,5 |
20 |
7 |
790 |
1,5 |
2 |
1 |
5 |
2,5 |
1 |
5 |
2 |
3 |
1 |
21 |
8 |
800 |
4 |
1.5 |
2,5 |
2 |
4 |
3,5 |
2 |
1,5 |
1 |
- |
22 |
9 |
810 |
2 |
3 |
1 |
1,5 |
1,5 |
2 |
1,5 |
4 |
3 |
2,5 |
23 |
10 |
820 |
1 |
5 |
2 |
4 |
1,5 |
3 |
1 |
2,5 |
2 |
- |
24 |
11 |
830 |
3,5 |
1,5 |
1 |
3 |
2 |
2,5 |
2 |
5 |
1,5 |
1 |
25 |
12 |
840 |
2,5 |
2 |
5 |
1,5 |
1 |
2 |
4 |
2 |
1,5 |
3 |
26 |
13 |
850 |
1 |
1,5 |
3 |
2 |
4 |
2,5 |
5 |
3 |
1 |
2,5 |
Рисунок 1 - Варианты структурных надёжностных схем
1)

2)

3)

4)

5)

6)

7)
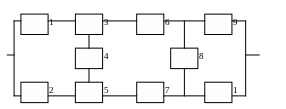
8)

9)
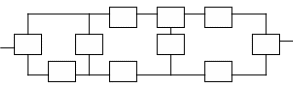
10)

11)
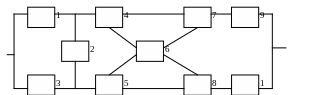
12)

13)