3 Второстепенная балка

3.1 Расчетная схема

Конструктивно второстепенная балка опирается на несущие стены или на контурные обвязочные балки и главные балки.

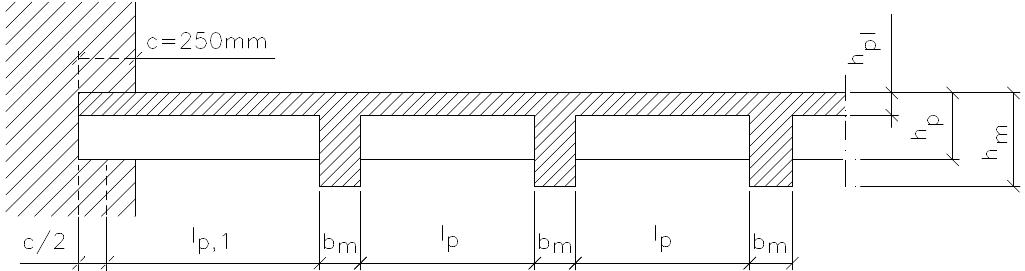
Рис. 2.5. Второстепенная балка, опертая на стену и главные балки:

с - длина опорного участка второстепенной балки; h_pl, h_p, h_m - высота плиты, второстепенной и главной балок; l_p,1 , l_p - расчетные длины первого и средних пролетов

Расчетные пролеты принимаются так же, как и у плиты: для крайних пролетов - расстоянию от центра тяжести опорной поверхности до ближайшей грани главной балки, а для средних - расстоянию между главными балками в свету. Длину опорного участка на стене принимают равной 250 мм, исходя из условия заводки продольной арматуры за грань опоры не менее 15d, где d - диаметр арматурного стержня.

В качестве расчетной схемы принимается пятипролетная (если фактическое количество пролетов больше или равно пяти) неразрезная балка таврового сечения.

Рис. 2.7. К определению размеров сечения второстепенной балки:

b_fp - ширина сжатой полки тавра; b_f1,p - ширина свеса полки; b_p - ширина ребра; h_fp - толщина полки

Для того, чтобы сечение балки можно было считать тавровым, свесы полки должны изгибаться так же, как и ребро. Это условие перестает выполняться при больших свесах, вследствие чего они оказываются менее напряженными. Поэтому СНиП требуют ограничения свесов полок тавровых сечений:

при h_fp  0,1h _p b_f1,p  6h_fp  

при h_fp  0,1h _p b_f1,p  l _p  6   (2.13)

в любом случае b_f1,p  l _pl  2 . 

h_fp ≥ 0,1h _p = 0,08м ≥ 0,1∙0,5 = 0,05м

b_f1,p  l _p  6 =7,75/6 =1,29≥ 1

b_f1,p  l _pl  2 =0,9 ≤ 1,81/2=0,905

Ширина грузовой площади, как показано на рис. 1.1, принимается равной расстоянию между второстепенными балками в осях и не зависит от того, какая принята ширина полки сечения. Нагрузка на второстепенную балку состоит из:

- веса плиты на грузовой площади;

- веса ребра второстепенной балки;

- временной нагрузки на перекрытие.

Все нагрузки, распределенные по площади, приводятся к погонным нагрузкам.

При определении расчетных нагрузок нужно, как и для плиты, учитывать коэффициенты надежности: по постоянной нагрузке _fg, по временной нагрузке _fv и коэффициент надежности по назначению _n.

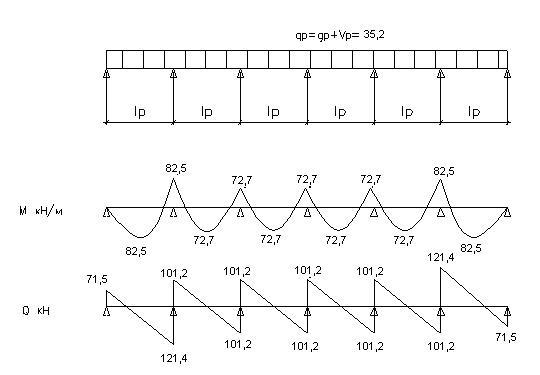
При расчете второстепенной балки нужно учесть, что временная нагрузка может менять свое положение. Вследствие этого отрицательные изгибающие моменты (при которых сжаты верхние волокна) могут возникать не только в опорных сечениях, но и в пролетах. Для их определения нужно кроме схемы, показанной на рис. 2.8, рассмотреть и такие схемы загружения, при которых возникают максимальные отрицательные пролетные моменты. Как показывает анализ работы неразрезной балки, максимальные отрицательные пролетные моменты возникают в ненагруженных пролетах в тех случаях, когда балка загружена полной нагрузкой через пролет.

Рис. 2.8. Расчетная схема второстепенной балки

q_p - полная погонная нагрузка на второстепенную балку;

g_p - постоянная погонная нагрузка (собственный вес плиты и ребра) собранная с грузовой площади;

v_p - временная погонная нагрузка, собранная с грузовой площади.

Поперечные силы вычисляются по формулам :

0. на крайних опорах -

;

0. на второй опоре слева -

;

0. на второй опоре справа и на средних опорах -

.

Выровненные изгибающие моменты вычисляются по формулам:

• в крайних пролетах и на вторых от края опорах -

;

• в средних пролетах и на средних опорах -

.

Однако, работа реальной балки отличается от работы идеализированной расчетной схемы:

1. в реальной балке полностью ненагруженных пролетов быть не может, так как постоянная нагрузка действует всегда;

2. опорные сечения реальной балки не могут свободно поворачиваться при деформации из-за частичного защемления их в главных балках, в то время как в расчетной схеме такому повороту не препятствуют шарнирные опоры.

Эти два отличия облегчают условия работы второстепенной балки по сравнению с идеализированной расчетной схемой. Поэтому для вычисления отрицательных пролетных изгибающих моментов расчетную схему загружают через пролет полной нагрузкой q_p, а “ненагруженные” пролеты - условной нагрузкой:

. (2.14)

Зная моменты, определим минимальную полезную высоту h₀:

a – расстояние от нижней грани плиты до центра тяжести рабочей арматуры.

Принимаем а = 35 мм.

Условие выполняется, тогда увеличение высоты балки не требуется и h = 0,5м.

Высоту второстепенной балки принимаем h₁=500мм.

Рассмотрим схемы загружения второстепенной балки для определения пролетных отрицательных изгибающих моментов

Рис 2.9. Схемы загружения второстепенной балки для определения

пролетных отрицательных изгибающих моментов

В наиболее нагруженных пролетах схем, показанных на рис. 2.9, максимальные изгибающие моменты будут такими же, как и в схеме 2.8, так как они равны моментам в пластических шарнирах. Для пролетов же, нагруженных нагрузкой q_p, эпюра изгибающих моментов строится на основе принципа суперпозиции:

1. строят эпюру М от опорных моментов;

2. строят эпюру М от пролетной нагрузки;

3. строят суммарную эпюру М.

Рассмотрим 1^ый пролет:

Рис. 2.10. Эпюра М для первого пролета схемы на рис. 2.9, b)

M_A=0.

М₁=

Рассмотрим 2^ой пролет:

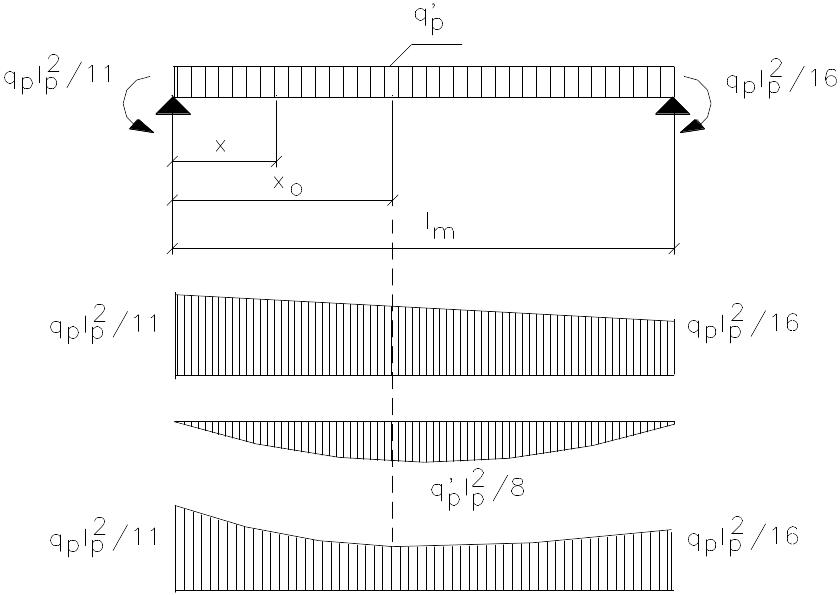
Рис 2.11. Эпюра М для второго пролета схемы на рис. 2.9, a.

Рассмотрим средний пролет:

Объединяя положительные и отрицательные эпюры моментов для двух схем загружения, получим огибающую эпюру моментов, показанную на рис. 2.12.

Рис. 2.12. Огибающая эпюра М для второстепенной балки